
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Произвольный треугольник
- Признаки равенства треугольников.
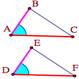
| I признак.
АВ = DE
AC = DF
 ÐA = ÐD
ß
DABC=DDEF ÐA = ÐD
ß
DABC=DDEF
| 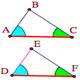
| II признак. AC = DF ÐA = ÐD ÐC = ÐF ß DABC=DDEF | 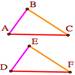
| III признак.
AC = DF
AB = DE
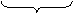  BC = EF
⇓
DABC=DDEF BC = EF
⇓
DABC=DDEF
|
2.  Теорема косинусов.
Теорема косинусов.
Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:

3.  Теорема синусов.
Теорема синусов.
Отношение любой стороны треугольника к синусу противоположного угла равно диаметру описанной около этого треугольника окружности.
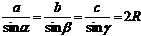
4. Площадь треугольника.
-
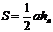 или
или  или
или 
-

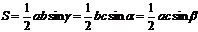
- S = p × r, где

-

- Формула Герона:

5.  Биссектриса в произвольном треугольнике.
Биссектриса в произвольном треугольнике.
- Биссектрисы треугольника пересекаются в одной точке – центре вписанной в треугольник окружности.
-
 Биссектриса, проведённая из вершины треугольника, делит противоположную сторону треугольника на отрезки, пропорциональные боковым сторонам.
Биссектриса, проведённая из вершины треугольника, делит противоположную сторону треугольника на отрезки, пропорциональные боковым сторонам. -

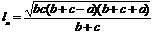
la-биссетриса, проведённая к стороне а.
6. Медиана в произвольном треугольнике.
- Медианы треуогольника пересекаются в одной точке и делятся точкой пересечения в отношении 2 к 1, считая от вершины.

-
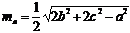 , где ma – медиана, проведённая к стороне а.
, где ma – медиана, проведённая к стороне а.
7. Определение подобных треугольников:
DABC~DA'B'C'ÛАВ/A'B', АС/A'С', ВС/B'C', ÐA=ÐA', ÐB=ÐB', ÐC=ÐC'.
8. Признаки подобия треугольников.

| I признак.
ÐA = ÐA'
 ÐC = ÐC'
ß
DABC~DA'B'C' ÐC = ÐC'
ß
DABC~DA'B'C'
| 
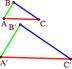
| II признак.
∠C=∠C'
  ß DABC~DA'B'C
ß DABC~DA'B'C
| 
| III признак.
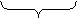  ß
DABC~DA'B'C'
ß
DABC~DA'B'C'
|
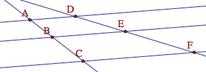
9. 
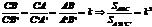 Отношение площадей подобных фигур.
Отношение площадей подобных фигур.
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
DABC~DA'B'C'Þ
10. Теорема Фалеса.
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
AD II BE, BE II CF Þ 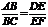
Не нашли, что искали? Воспользуйтесь поиском: