Прямоугольный треугольник. 11. Признаки равенства прямоугольных треугольников.

11. Признаки равенства прямоугольных треугольников.

a. По двум катетам: a = a ', b = b ' Þ DABC=DA'B'C'

b. По катету и гипотенузе:

a = a ', с = с ' Þ DABC=DA'B'C'

c. По катету и острому углу:

a = a ', b = b ' Þ DABC=DA'B'C'

d. По гипотенузе и острому углу: с = c ', b = b ' Þ DABC=DA'B'C'

12. Теорема Пифагора. Квадрат гипотенузы равен сумме квадратов катетов: с ² = a ² + b ²

13. Соотношения между сторонами и углами прямоугольного треугольника.

a. Синус острого угла в прямоугольном треугольнике – отношение противолежащего катета к гипотенузе:

b. Косинус острого угла в прямоугольном треугольнике – отношение прилежащего катета к гипотенузе:

c. Тангенс острого угла в прямоугольном треугольнике – отношение противолежащего катета к прилежащему:

d. Котангенс острого угла в прямоугольном треугольнике – отношение прилежащего катета к противолежащему:

14. Пропорциональные отрезки в прямоугольном треугольнике.
Если в прямоугольном треугольнике проведена высота к гипотенузе, то:

a. DABC~DCBH Þ ;

b. DABC~DCBH Þ ;

c. DACH~DCBH Þ ;

15. Радиус вписанной и описанной окружности.

a. R = c /2 – радиус описанной окружности равен половине гипотенузы и следовательно медиана, проведённая к гипотенузе, равна её половине.

b. или r = p – c, где .

c. R + r = (a + b)/2.

Четырёхугольники

16. 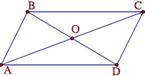Параллелограмм.

a. Определение. Параллелограмм – это четырёхугольник, в котором противоположные стороны попарно параллельны.

b. Свойства параллелограмма. Если четырёхугольник – параллелограмм, то:

· его противоположные стороны и углы равны;

· диагонали точкой пересечения делятся пополам.

c. Признаки параллелограмма.

· Если в четырёхугольнике противоположные стороны равны, то этот четырёхугольник – параллелограмм.

· Если в четырёхугольнике противоположные углы равны, то этот четырёхугольник – параллелограмм.

· Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.

· Если в четырёхугольнике две противоположные стороны равны и параллельны, то этот четырёхугольник – параллелограмм: AB = CD, AB II CD Þ ABCD – параллелограмм.

d. Площадь параллелограмма.

i. S = AD×BH, где BH – высота;

ii. S = AB×AD×sinA

e. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: AC² + BD² = 2AB² + 2AD².

17. Прямоугольник - это параллелограмм, у которого есть хотя бы один прямой угол.

a. Свойства прямоугольника.

· Диагонали прямоугольника равны.

· Около прямоугольника можно описать окружность. Центр описанной окружности – точка пересечения диагоналей прямоугольника.

18. Ромб – это параллелограмм, у которого все стороны равны.

a. Свойства ромба.

· Диагонали ромба взаимно перпендикулярны и являются биссектрисами углов ромба.

· В ромб можно вписать окружность. Центр вписанной окружности – точка пересечения диагоналей ромба.

b. Площадь ромба.

· S=1/2AC×BD – площадь равна половине произведения диагоналей.

19. Квадрат – это прямоугольник, у которого все стороны равны.

a. Свойства квадрата.

· Квдрат наследует все свойства параллелограмма, прямоугольника и ромба.

· Около квадрата можно описать окружность и в квадрат можно вписать окружность.

20.
Трапеция -четырёхугольник, у которого две стороны параллельны, а две другие нет называется трапецией.

a. Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

b. Площадь трапеции равна произведению полусуммы оснований на высоту трапеции.

21. Равнобедренная трапеция – трапеция, у которой боковые стороны равны.

· Углы при основании равы.

· Высота, проведённая из вершины верхнего основания к нижнему, делит нижнее основание на отрезки, больший из которых равен средней линии трапеции (AH = MN).

· Около любой равнобедренной трапеции можно описать окружность. Центр находится на пересечении серединных перпендикуляров к сторонам трапеции.

22. Произвольный четырёхугольник.

a. Площадь произвольного четырёхугольника равна половине произведения его диагоналей на синус угла между ними:

b. В четырёхугольник можно вписать окружность, если суммы его противоположных сторон равны, то есть AB+CD = AD+BC.

c. Около четырёхугольника можно описать окружность, если суммы противоположных углов этого четырёхугольника равны.

Окружность.

a. Касательная к окружности – прямая, которая имеет с окружностью, только одну общую точку.

· Радиус, проведённый в точку касания, перепендикулярен касательной.

· Отрезки касательных, проведённых из одной точке к окружности, равны.

· Угол между касательной и хордой равен половине дуги окружности, стягиваемой хордой:

b. Секущая – прямая, которая пересекает окружность в двух точках.

· Свойство секущих: .

· Свойство секущей и касательной: .

· Свойство хорд: хорды точкой пересечения делятся на отрезки так, что произведение отрезков одной хорды равно произведению отрезков другой хорды.

c. Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекаю окружность.

d. Центральный угол – это угол, вершина которого является центром окружности.

· Вписанный угол равен половине центрального угла, опирающегося на одну и ту же дугу: ÐMAN = 1/2ÐMON.

Не нашли, что искали? Воспользуйтесь поиском: