Окружность, круг. Хорды, дуги

Основные понятия

11.1. Найти величины смежных углов, если:

а) один из них больше второго на 30^о;

б) один из них в 8 раз меньше другого;

в) разность их величин составляет 44^о;

г) отношение их величин равно 2.

Ответы: а) 75^о и 105^о; б) 20^о и 160^о; в) 112^о и 68^о; г) 120^о и 60^о.

11.2. В каждом из смежных углов AOB и BOC проведены соответственно биссектрисы OD и OM. Найти углы DOB и BOM, если разность их величин равна 14^о.

Ответ: 52^о, 38^о.

11.3. В каждом из смежных углов AOB и BOC проведены соответственно биссектрисы OD и OM. Найти величины углов AOD и MOC, если они относятся как 2: 3.

Ответ: 34^о, 54^о.

11.4. В каждом из смежных углов АОС и СОВ проведены внутренние углы соответственно ОМ и ОР так, что Найти величины углов MOA и POB, если величина угла MOA в четыре раза больше величины угла POB.

Ответ: 112^о, 48^о.

11.5. Углы САВ и ВАD смежные. Найти величину угла между перпендикуляром, проведенным из точки А к прямой СD, и биссектрисой угла САВ, если

Ответ: 40^о.

Ответ: а) 50^о и 130^о; б) 80^о и 100^о; в) 60^о и 120^о.

11.7. Один из двух внутренних односторонних углов при параллельных прямых и секущей на 60^о меньше другого. Найти больший из этих углов.

Ответ: 120^о.

11.8. Один из двух внутренних углов при параллельных прямых и секущей в 17 раз больше другого. Найти меньший из этих углов.

Ответ: 10^о.

Треугольники

11.9. Углы треугольника пропорциональны числам 3, 7 и 8. Найти наибольший угол треугольника.

Ответ: 80^о.

11.10. Угол при вершине равнобедренного треугольника на 60^о больше угла при основании. Найти угол при основании треугольника.

Ответ: 40^о.

11.11. В равнобедренном треугольнике угол, смежный с углом при вершине треугольника, равен 70^о. Найти угол при основании треугольника.

Ответ: 35^о.

11.12. Гипотенуза прямоугольного треугольника равна 26 см, а его катеты относятся как 5: 12. Найти больший катет треугольника.

Ответ: 24 см.

11.13. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза больше другого катета на 8 см. Найти площадь треугольника.

Ответ: 30 см².

11.14. Найти площадь равнобедренного треугольника по его гипотенузе, равной см.

Ответ: 8 см².

11.15. Катеты прямоугольного треугольника равны 6 см и 8 см. Найти длину медианы, проведенной к гипотенузе.

Ответ: 5 см.

11.16. В прямоугольном треугольнике медиана, опущенная из вершины прямого угла, равна одному из катетов. Найти меньший угол треугольника.

Ответ: 30^о.

11.17. В прямоугольном треугольнике острые углы относятся как 1: 2. Больший катет равен см. Найти радиус описан­ной окружности.

Ответ: 4 см.

11.18. В прямоугольном треугольнике АВС Около треугольника описана окружность с центром в точке О. Найти величину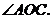

Ответ: 100^о.

11.19. Диаметр окружности, описанной около прямоугольного треугольника, равен 10 см, а один из катетов равен 6 см. Найти другой катет.

Ответ: 8 см.

11.20. Катет и гипотенуза прямоугольного треугольника равны соответственно 10 см и 26 см. Найти радиус вписанной окружности.

Ответ: 4 см.

11.21. В прямоугольном треугольнике гипотенуза равна 20 см, а косинус одного угла равен 0,8. Найти больший катет.

Ответ: 16 см.

11.22. В прямоугольном треугольнике тангенс одного угла равен 0,6, а меньший катет равен 3 см. Найти больший катет.

Ответ: 5 см.

11.23. В прямоугольном треугольнике один из катетов равен 3 см, а котангенс прилежащего угла – 0,75. Найти гипотенузу.

Ответ: 5 см.

11.24. Из вершины прямого угла А прямоугольного треугольника к гипотенузе проведены медиана АМ и высота АК. Найти длину отрезка МК, если катеты равны 6 см и см.

Ответ: 0,5 см.

11.25. Катеты прямоугольного треугольника относятся как 1: 3. Найти высоту треугольника, опущенную из вершины прямого угла, если гипотенуза равна 40 см.

Ответ: 12 см.

11.26. Из одной точки проведены перпендикуляр и две наклонные длиной 10 см и 17 см к данной прямой. Проекции наклонных относятся как 2: 5. Найти длину перпендикуляра.

Ответ: 8 см.

11.27. В прямоугольный треугольник с катетами 3 см и 5 см вписан квадрат, имеющий с треугольником общий прямой угол. Найти периметр квадрата.

Ответ: 7,5 см.

11.28. В прямоугольный треугольник с углом 60^о вписан ромб так, что угол в 60^о у них общий, остальные три вершины ромба лежат на сторонах треугольника. Найти длину общего катета, если длина стороны ромба равна 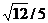см.

Ответ: 1,8 см.

11.29. В равнобедренный прямоугольный треугольник впи­сан квадрат таким образом, что две его вершины лежат на гипо­тенузе, а две другие – на катетах. Сторона квадрата равна 3 см. Найти длину гипотенузы.

Ответ: 7 см.

11.30. В равнобедренный прямоугольный треугольник впи­сан прямоугольник таким образом, что он имеет с треугольни­ком общий прямой угол. Периметр этого прямоугольника равен 25 см. Найти катет треугольника.

Ответ: 12,5 см.

11.31. В равнобедренный прямоугольный треугольник впи­сан ромб так, что один острый угол у них общий и все четыре вершины ромба лежат на сторонах треугольника. Найти сторону ромба, если длина катета равна см.

Ответ: 0,4 см.

11.32. Гипотенуза прямоугольного треугольника равна 10 см, а проекция меньшего катета на гипотенузу равна 3,6 см. Найти радиус окружности, вписанной в этот треугольник.

Ответ: 2 см.

11.33. В прямоугольный треугольник вписана окружность. Точка касания окружности и гипотенузы делит ее на отрезки 3 см и 10 см. Найти больший катет.

Ответ: 12 см.

11.34. Радиусы вписанной и описанной окружностей пря­моугольного треугольника равны соответственно 2 см и 5 см. Найти больший катет треугольника.

Ответ: 8 см.

11.35. Окружность касается большего катета прямоуголь­ного треугольника и проходит через вершину противолежащего острого угла. Найти радиус окружности, если ее центр лежит на гипотенузе, а длины катетов равны 3 см и см.

Ответ: 2,1 см.

11.36. Найти радиус круга, описанного около равностороннего треугольника со стороной см.

Ответ: 12 см.

11.37. Площадь правильного треугольника равна см². Найти длину его биссектрисы.

Ответ: 1 см.

11.38. В равностороннем треугольнике высота равна 9 см. Найти радиус вписанной в треугольник окружности.

Ответ: 3 см.

11.39. Радиус окружности равен 10 см. Найти длину медианы вписанного в нее правильного треугольника.

Ответ: 15 см.

11.40. Около равностороннего треугольника описана окруж­ность радиуса см, через центр которой проведена прямая, параллельная одной из сторон треугольника. Найти длину отрезка прямой, заключенного между двумя другими сторонами треугольника.

Ответ: 4 см.

11.41. В равнобедренном треугольнике боковая сторона равна 5 см, а косинус угла при основании равен 0,6. Найти радиус вписанного круга.

Ответ: 1,5 см.

11.42. В треугольнике АВС известно, что угол А равен 45^о и котангенс угла В равен 0,25. Найти сторону АВ, если площадь треугольника равна 10 см².

Ответ: 5 см.

11.43. Серединный перпендикуляр к боковой стороне АВ равнобедренного треугольника АВС пересекает сторону АС в ее середине О. Найти расстояние ОВ, если длина АС равна 20 см.

Ответ: 10 см.

11.44. Найти радиус окружности, описанной около равнобедренного треугольника, боковая сторона которого равна см, а угол при вершине 60^о.

Ответ: 4 см.

11.45. Периметр равнобедренного треугольника АВС (АВ = ВС) равен 110 см, а отрезок, соединяющий середины боковых сторон, равен 15 см. Найти длину боковой стороны.

Ответ: 40 см.

11.46. Угол при вершине равнобедренного треугольника АВС (АВ = ВС) равен 53^о, а его площадь равна 360 см². Найти длину боковой стороны треугольника (sin 53^о = 0,8).

Ответ: 30 см.

11.47. В равнобедренный треугольник вписана окружность радиуса см. Угол при основании 60^о. Найти длину основания треугольника.

Ответ: 6 см.

11.48. Основание равнобедренного треугольника в 3 раза меньше его боковой стороны, а его периметр равен 14 см. Найти длину основания треугольника.

Ответ: 2 см.

11.49. В равнобедренном треугольнике основание равно см, угол при вершине 120^о. Определить проекцию высоты, проведенной к основанию, на боковую сторону.

Ответ: 3 см.

11.50. Найти высоту, опущенную на боковую сторону равнобедренного треугольника, если высота, проведенная к основанию, равна см и угол при вершине В равен 120^о.

Ответ: 12 см.

11.51. В равнобедренном треугольнике углы при основании равны 30^о, а высота, опущенная на это основание, равна 3 см. Найти радиус окружности, описанной около треугольника.

Ответ: 6 см.

11.52. Найти радиус окружности, описанной около равно­бедренного треугольника с основанием 16 см и высотой 4 см.

Ответ: 10 см.

11.53. Биссектриса внешнего угла равнобедренного треуголь­ника АВС при основании АС образует с основанием угол 126^о. Найти величину угла АВС.

Ответ: 36^о.

11.54. Внутри треугольника АВС к стороне ВС проведена прямая AD так, что угол CAD равен углу ACD. Периметры треугольников ABC и ABD равны 18 см и 11 см соответственно. Найти длину AC.

Ответ: 7 см.

11.55. Радиус окружности, описанной около треугольника АВС, равен 5, сторона АВ равна 5 см, высота ВН равна 4 см. Найти длину стороны ВС.

Ответ: 8 см.

11.56. В треугольник вписан ромб, угол которого совпадает с углом треугольника. Стороны треугольника, заключающие этот угол, равны 12 см и 18 см. Найти сторону ромба.

Ответ: 7,2 см.

11.57. В треугольнике одна сторона равна см и противо­лежащий ей угол равен 30^о, вторая сторона равна см. Най­ти третью сторону.

Ответ: 3 см.

11.58. В треугольнике известны длины двух сторон: 6 см и 9 см, и угол между ними 30^о. Найти площадь этого треугольника.

Ответ: 13,5 см².

11.59. В треугольнике АВС величина угла при вершине С равна π/6. Найти синус угла В, если АС = 12,3 см и АВ = 61,5 см.

Ответ: 0,1.

11.60. В треугольнике АВС углы В и С равны соответст­венно π/3 и π/4. Найти длину стороны АС, если АВ = см.

Ответ: 10,5 см.

11.61. В треугольнике АВС проведена медиана АК, равная см и составляющая со стороной АС угол 30^о. Найти ВС, если угол ВСА равен 45^о.

Ответ: 6,5 см.

11.62. В треугольнике АВС даны три стороны см, см, см. Найти медиану

Ответ: 2 см.

11.63. Найти меньшую высоту треугольника со сторонами 13 см, 14 см и 15 см.

Ответ: 11,2 см.

Четырехугольники

11.64. В окружность радиуса см вписан квадрат. Из одной вершины этого квадрата проведены две хорды, стягивающие дуги по 120^о. Найти длину отрезка диагонали квадрата, заключенного между этими хордами.

Ответ: 6 см.

11.65. В прямоугольнике ABCD проведена диагональ AC. Известно, что угол ACB в 8 раз меньше, чем угол CAB. Найти угол CAB.

Ответ: 80^о.

11.66. Найти большую сторону прямоугольника площадью 400 см², если его стороны относятся как 4: 1.

Ответ: 40 см.

11.67. Высота, опущенная на диагональ прямоугольника, делит ее на отрезки длиной 4 см и 9 см. Найти площадь прямоугольника.

Ответ: 78 см.

11.68. На диагональ АС прямоугольника АВСD опущены высоты ВЕ и DТ. Найти площадь прямоугольника, если ЕТ = 16 см, а ВЕ = 6 см.

Ответ: 120 см.

11.69. Сторона ромба равна 5 см, а меньшая диагональ 6 см. Найти большую диагональ.

Ответ: 8 см.

11.70. Диагонали ромба равны 12 см и 16 см. Найти сторону ромба.

Ответ: 10 см.

11.71. Найти тупой угол ромба, если высота, проведенная из его вершины, делит противоположную сторону пополам.

Ответ: 120^о.

11.72. Диагональ ромба равна его стороне. Найти больший угол ромба.

Ответ: 120^о.

11.73. Периметр ромба равен 24 см. Высота равна 3 см. Найти острый угол ромба.

Ответ: 30^о.

11.74. Вычислить периметр ромба, высота которого равна см, а острый угол в 2 раза меньше тупого.

Ответ: 8 см.

11.75. В ромбе длины диагоналей равны 10 см и 15 см. Найти его площадь.

Ответ: 75 см.

11.76. Найти площадь ромба со стороной 4 см, если радиус вписанной окружности равен 1,5 см.

Ответ: 12 см².

11.77. Сторона ромба равна 4 см. Радиус окружности, вписан­ной в этот ромб, равен 1 см. Найти величину острого угла ромба.

Ответ: 30^о.

11.78. Высота параллелограмма ABCD, опущенная на сторону AD из точки B, равна см. Найти площадь параллелограмма, если диагональ BD = 7 см, а угол BAD = 60^о.

Ответ: см².

11.79. Периметр параллелограмма равен 92 см. Одна из его сторон больше другой на 4 см. Найти большую сторону параллелограмма.

Ответ: 25 см.

11.80. Сумма двух противоположных углов параллелограм­ма равна 94^о. Найти больший угол параллелограмма.

Ответ: 133^о.

11.81. Площадь параллелограмма равна 120 см², а его стороны 15 см и 10 см. Найти большую высоту параллелограмма.

Ответ: 12 см.

11.82. Площадь параллелограмма равна 150 см², а его высоты 25 см и 10 см. Найти периметр параллелограмма.

Ответ: 22 см.

11.83. Стороны параллелограмма равны 6 см и 16 см, а его ту­пой угол равен 120^о. Найти меньшую диагональ параллелограмма.

Ответ: 14 см.

11.84. Стороны параллелограмма равны см, см. Найти сумму квадратов длин диагоналей параллелограмма.

Ответ: 30 см.

11.85. Диагонали параллелограмма равны 17 см и 19 см. Одна сторона равна 10 см. Найти другую сторону.

Ответ: 15 см.

11.86. Одна из диагоналей параллелограмма, равная см, составляет с основанием угол 60^о. Найти длину второй диагонали, если она составляет с тем же основанием угол 45^о.

Ответ: 13,5 см.

11.87. В параллелограмме боковая сторона равна 8 см, а острый угол при основании равен 30^о. Найти проекцию высоты, опущенной на основание, на боковую сторону.

Ответ: 2 см.

11.88. Периметр равнобедренной трапеции равен 36 см, а средняя линия равна 10 см. Найти боковую сторону трапеции.

Ответ: 8 см.

Ответ: 50 см.

11.90. В равнобедренной трапеции основания равны 6 см и 10 см. Диагональ равна 10 см. Найти площадь трапеции.

Ответ: 48 см².

11.91. Разность двух оснований равнобедренной трапеции равна 3 см. Синус угла при основании трапеции равен 0,8. Найти длину боковой стороны трапеции.

Ответ: 2,5 см.

11.92. Периметр описанной около окружности трапеции равен 30 см. Найти ее среднюю линию.

Ответ: 7,5 см.

11.93. В трапеции, площадь которой равна 161 см², высота равна 7 см, а разность параллельных сторон равна 11 см. Найти длину большего основания.

Ответ: 28,5 см.

11.94. В прямоугольной трапеции меньшая диагональ равна 15 см и перпендикулярна большей боковой стороне. Меньшая сторона равна 12 см. Найти большее основание трапеции.

Ответ: 25 см.

Ответ: 0,875 см.

11.96. Равнобедренная трапеция описана около круга. Боковая сторона трапеции делится точкой касания на отрезки длиной 12 см и 48 см. Найти площадь трапеции.

Ответ: 2880 см².

11.97. Средняя линия равнобедренной трапеции, описанной около круга, равна 68 см. Найти радиус этого круга, если нижнее основание трапеции больше верхнего на 64 см.

Ответ: 30 см.

11.98. В равнобедренной трапеции диагональ делит острый угол пополам. Найти среднюю линию трапеции, если ее периметр равен 48 см, а большее основание равно 18 см.

Ответ: 14 см.

11.99. Меньшее основание равнобокой трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне. Определить углы трапеции.

Ответ: 60^о, 120^о.

11.100. Основания трапеции равны 12 см и 6 см. Найти отношение площадей частей, на которые делится трапеция ее средней линией.

Ответ: 5/7.

11.101. Диагональ равнобедренной трапеции образует с основанием угол, равный 30°. Найти площадь трапеции, если ее высота равна 5 см.

Ответ: см².

11.102. В равнобедренной трапеции основания равны 7 см и 25 см, а диагональ равна 20 см. Найти площадь трапеции.

Ответ: 192 см².

11.103. В трапеции ABCD основаниями являются стороны BC и AD, O – точка пересечения диагоналей, AD = 18 см, AO = 10 см и ОC = 5 см. Найти длину BC.

Ответ: 9 см.

11.104. В четырехугольнике ABCD прямая AC делит каждый из углов BAD и BCD пополам. Найти периметр четырехуголь­ника, если P_ADC = 15 см, а равно AC 5 см.

Ответ: 20 см.

Окружность, круг. Хорды, дуги

11.105. В окружности радиуса 26 см проведена хорда, равная 28 см. Найти длину отрезка, соединяющего середину хорды с центром окружности.

Ответ: 10 см.

11.106. Найти расстояние от центра окружности до хорды, равной 6 см, если радиус окружности равен 5 см.

Ответ: 4 см.

11.107. Хорда пересекает диаметр под углом 30° и делит его на два отрезка длиной 2 см и 6 см. Найти расстояние от центра круга до хорды.

Ответ: 2 см.

11.108. В окружности с центром в точке О проведены хорда AB и радиус OD, которые пересекаются в точке C, причем известно, что см, см. Найти хорду.

Ответ: 80 см.

11.109. На окружности с центром О лежит точка В. АВ – хорда, АС – касательная, Найти угол АОВ.

Ответ: 70°.

11.110. В угол величиной 60° вписана окружность. Найти расстояние от центра окружности до вершины угла, если радиус окружности равен 7,5 см.

Ответ: 15 см.

11.111. В круговой сектор, дуга которого содержит 60°, вписан круг. Найти отношение площади этого круга к площади сектора.

Ответ: 2/3.

11.112. В круговой сектор вписана окружность, радиус которой в три раза меньше радиуса сектора. Найти величину центрального угла сектора.

Ответ: 60°.

11.113. К окружности радиуса 5 см в точке В проведена касательная, на которой отмечена точка А на расстоянии 12 см от точки В. Найти расстояние от точки А до центра окружности.

Ответ: 13 см.

11.114. Длина окружности равна 4π см. Найти площадь квадрата, вписанного в эту окружность.

Ответ: 8 см².

11.115. В круг вписан квадрат со стороной, равной см. Найти площадь круга.

Ответ: 2 см².

11.116. Найти площадь круга, если известно, что длина окружности круга вдвое меньшей площади равна 6π см.

Ответ: 18 см².

11.117. Центральный угол окружности на 50° больше вписанного угла, опирающегося на ту же дугу. Найти величину дуги.

Ответ: 100°.

11.118. Окружность радиуса 2 см разогнута в дугу радиуса 15 см. Найти центральный угол.

Ответ: 48°.

11.119. Круг радиуса 6 см делится концентрической окружностью на две части – на круг радиуса r и кольцо, площади которых относятся как 1: 3. Найти r.

Ответ: 3 см.

11.120. Площадь кругового сектора равна 0,1π см², радиус круга равен 1 см. Найти величину угла, опирающегося на дугу сектора с вершиной на окружности.

Ответ: 18°.

11.121. Две окружности, каждая из которых вписана в угол величиной 60°, касаются друг друга внешним образом. Найти расстояние от точки касания окружностей до стороны угла, если радиус большей окружности равен 23 см.

Ответ: 11,5 см.

11.122. Общая хорда двух пересекающихся окружностей видна из их центров под углами 90° и 120°. Найти расстояние между центрами окружностей, лежащими по одну сторону от хорды, если длина хорды равна 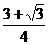см.

Ответ: 0,25 см.

11.123. Из точки К, лежащей на окружности, проведены касательная к окружности и хорда КА. Угол между ними равен 60°. Найти длину меньшей дуги, отсекаемой хордой КА, если радиус окружности равен см.

Ответ: 2 см.

11.124. Из точки А, лежащей вне круга, проведены касатель­ная к кругу и секущая. Найти, во сколько раз отрезок секущей, лежащей внутри круга, больше отрезка секущей, находящегося вне круга, если расстояние от точки А до точки касания в 3 раза больше, чем длина отрезка, лежащего вне круга.

Ответ: в8 раз.

11.125. В окружности радиуса см из одного конца диаметра проведена касательная, а из другого – хорда, стягивающая дугу в 120°. Хорда продолжена до пересечения с касательной. Найти внешний отрезок секущей.

Ответ: 1 см.

11.126. Длина окружности, в которую вписан правильный шестиугольник, равна см. Найти длину окружности, вписанной в этот шестиугольник.

Ответ: 1,5 см.

11.127. В окружности с центром О проведены диаметр АВ и хорда ВС, угол АОС равен 60°. Найти угол АВС.

Ответ: 30°.

Не нашли, что искали? Воспользуйтесь поиском: