
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Багатогранники. Площі поверхонь. Об’єм багатогранників
Призма. Якщо в двох паралельних площинах α і β розташовані рівні п -кути, відповідні сторони яких попарно Паралельні, а відповідні вершини з’єднані відрізками, те отриманий у такий спосіб багатогранник називається призмою (рис. 58). Багатокутники, що лежать у площинах а і р, називаються основами призми. Чотирикутники АВВ 1 А 1, ВВ 1 С 1 С і т. д. називаються бічними гранями призми і вони являються паралелограмами; відрізки AA 1, BB 1 і т. д. називаються бічними ребрами призми. Всі бічні ребра призми рівні і Паралельні. Висотою призми називається відстань між площинами α і β, тобто довжина перпендикуляра, опущеного з будь-якої точки площини α на площину β.
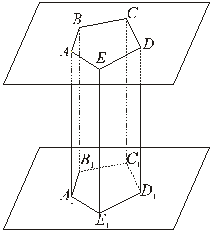
Рис. 58
Площа бічної поверхні призми дорівнює добутку периметра перпендикулярного перетину призми на довжину бічного ребра.
Об’єм призми дорівнює добутку площі підстави на висоту призми або площі перпендикулярного перетину на довжину бічного ребра:
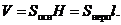
Прямою називається призма, бічне ребро якої перпендикулярно площині підстави.
Правильною називається пряма призма, у підставі якої лежить правильний багатокутник.
Окремими випадками призми є прямокутний паралелепіпед — пряма призма, у підставі якої лежить прямокутник, і куб — правильна призма, в основі якої лежить квадрат. Об’єм прямокутного паралелепіпеда дорівнює добутку довжин трьох ребер, що виходять з однієї вершини.
Піраміда. Нехай на площині α лежить опуклий багатокутник А 1 A 2 A 3… Аn, а точка S не належить площини α. З’єднавши точку S з вершинами багатокутника, одержимо багатогранник, що називається п -кутовою пірамідою (рис. 59). Багатокутник А 1 A 2 A 3... Аn називається основою піраміди. Висотою піраміди називається відрізок перпендикуляра, опущеного з вершини S на площину підстави.
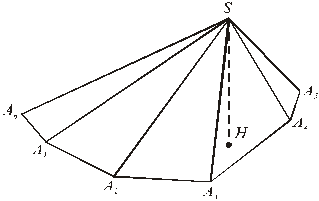
Рис. 59
Правильної називається піраміда, у підставі якої лежить правильний багатокутник, а висота проходить через центр кола, описаної біля підстави.
Об’єм довільної піраміди
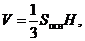
де 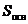 — площа підстави, Н — висота.
— площа підстави, Н — висота.
Вписані й описані сфери. Сфера називається описаної біля багатогранника, якщо вона проходить через усі його вершини. Сфера називається вписаної в багатогранник, якщо вона стосується всіх його граней.
Теорема 1. Для того щоб біля піраміди можна було описати сферу, необхідно і досить, щоб біля багатокутника, що лежить в основі, можна було описати окружність.
Теорема 2. Навколо будь-якої правильної піраміди можна описати сферу й в неї можна вписати сферу.
Центр сфери, описаної біля піраміди, допомагають знайти наступні два твердження.
1. Множина точок простору, рівновіддалених від двох даних точок А і В, є площина, що проходить через середину відрізка АВ і перпендикулярна йому.
2. Нехай точка О — центр кола, що описана біля плоского багатокутника А 1 A 2 A 3... Аn. Тоді множина точок простору, рівновіддалених від усіх вершин багатокутника А 1 A 2 A 3… Аn, є перпендикуляр до площини багатокутника, що проходить через точку О.
Наслідок. Якщо навколо багатокутника, що лежить у підставі піраміди SА 1 A 2... Аn, можна описати окружність, центром якої є точка О, те центр описаної біля піраміди сфери буде знаходитися на перетинанні перпендикуляра до площини основи, вставленого з точки О, і площини, що проходить через середину якого-небудь бічного ребра піраміди (наприклад, A 1 S), перпендикулярної цьому ребру.
Центр вписаної в многогранник сфери лежить на перетинанні бісекторних площин усіх двогранних кутів багатогранника.
Теорема 3. У довільну трикутну піраміду можна вписати сферу.
Об”єм багатогранника
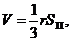
де r — радіус вписаної в багатогранник сфери, S П — площа повної поверхні багатогранника.
Правильним називається багатогранник, усієї грані якого є однаковими правильними багатокутниками.
Не нашли, что искали? Воспользуйтесь поиском: