Додаткова література. 2. Ремизов А.Н. Медицинская и биологическая физика

1. Биофизика / Под ред. Ю.А. Владимирова - М.: Медицина, 1983.

2. Ремизов А.Н. Медицинская и биологическая физика. - М: Висшая школа, 1996.

3. Чальш А.В. Неравновесньїе процессьі в физике и биологии. - К.: Наукова думка, 1997.

4. Чалий О.В. Синергетичні принципи освіти та науки. - К.: Віпол, 2000.

Завдання для самостійної роботи і перевірки кінцевого рівня знань

Після вивчення теоретичного матеріалу слід ознайоми­тись з еталонами розв'язку задач і виконати завдання для перевірки кінцевого рівня знань.

Типові задачі з еталонами розв'язків

Задача 1

Маємо 2 молекули в об'ємі, який розділений напів­проникною перегородкою. Намалювати можливі конфігу­рації в цій системі. Знайти: а) число мікростанів, тобто термодинамічну ймовірність; б) ентропію; в) ймовір­ність (частоту появи) кожної з конфігурацій.

Розв 'язок

Можливі конфігурації для системи з 2 молекул в заданому об'ємі представлені нарис. 5.12.

Рис. 5.12. Можливі конфігурації для молекул а і б в об'ємі з напівпроникною перегородкою.

Число мікростанів (термодинамічна ймовірність) дорів­нює

- для першої конфігурації

- для другої конфігурації

- для третьої конфігурації

Ентропія кожної з конфігурацій дорівнює

Ймовірність (частота появи) кожної з конфігурацій до­рівнює

Задача 2

Узагальнити закон Ома в диференціальній формі на випадок, коли в системі є ще й градієнт концентрації числа частинок.

Розв 'язок

Закон Ома в диференціальній формі має вигляд де 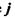- густина електричного струму; 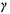- коефіцієнт електро­провідності; 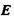- напруженість електричного поля.

Оскільки напруженість зв'язана відомим співвідношен­ням з градієнтом потенціалу електричного поля 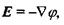то закон Ома набуває такого вигляду: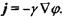

Згідно з лінійним законом термодинаміки необернених процесів, в присутності градієнта концентрації числа части­нок 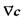маємо таке узагальнення закону Ома в диферен­ціальній формі:

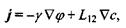
де 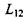- кінетичний коефіцієнт, що відповідає за перехрес­ний процес появи додаткового внеску в електричний струм за рахунок градієнта концентрації числа частинок.

Завдання для перевірки кінцевого рівня знань

1. Записати зміну ентальпії через зміну внутрішньої енергії, об'єму і тиску. Розглянути окремий випадок ізобарної системи.

2. Записати зміну вільної енергії Гіббса через зміну ентальпії, температури і ентропії. Розглянути окремий випадок ізотерміч­ної системи.

3. В об'ємі, що розділений напівпроникною перегородкою, знахо­диться 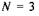молекули. Знайти число мікростанів (термодина­мічну ймовірність) і ймовірність (частоту появи) кожної з конфігурацій.

4. Знайти ентропію кожної з конфігурацій для задачі 3.

5. В об'ємі, що розділений напівпроникною перегородкою, знахо­диться молекули. Знайти число мікростанів (термодина­мічну ймовірність) і ймовірність (частоту появи) кожної з конфігурацій.

6. Знайти ентропію кожної з конфігурацій для задачі 5.

7. В об'ємі, що розділений напівпроникною перегородкою, знахо­диться молекули. Знайти число мікростанів (термодина­мічну ймовірність) і ймовірність (частоту появи) кожної з конфігурацій.

8. Знайти ентропію кожної з конфігурацій для задачі 7.

9. Написати вираз для потоку частинок при наявності різниці концентрації і температури. Розглянути окремий випадок відсут­ності потоку частинок у такій системі.

10.Написати вираз для потоку частинок при наявності різниці концентрації і тиску. Розглянути окремий випадок відсутності потоку частинок у такій системі.

11.У системі є два градієнти (температури і концентрації) і два потоки (частинок і тепла). Записати відповідні лінійні закони і принцип симетрії кінетичних коефіцієнтів для такої системи.

12.Записати у загальному вигляді лінійний закон для густини електричного струму через мембрану. Взяти до уваги, що з обох сторін мембрани різні концентрації і потенціали електричного поля.

Не нашли, что искали? Воспользуйтесь поиском: