Примеры расчета аналитического метода определения координат

№ Вершины	КООРДИНАТЫ	РАЗНОСТЬ КООРДИНАТ	ПРОИЗВЕДЕНИе
+ -	Х	+ -	У	+ -		+ -		+ -		+ -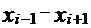
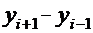
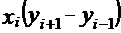
	+	36,83	+	29,76	-	200,62	-	219,55	-	5970,4512	-	8086,0265
	+	209,43	+	112,33	-	340,58	+	13,14	-	38257,3514	+	2751,9102
	+	377,41	+	42,90	-	278,34	+	209,37	-	11940,7860	+	79018,3317
	+	487,77	+	321,70	+	119,63	+	430,82	+	38484,9710	+	210141,0714
	+	257,78	+	473,72	+	478,96	+	10,18	+	226892,9312	+	2624,2064
	+	8,81	+	331,88	+	220,95	-	443,96	+	73328,8860	-	3911,2876
						+819,54 -819,54		+663,51 - 663,51		+338706,7882 - 56168,5886 282538,1996		+294535,5137 -11997,3141 28253,1996

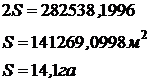
Графический способ

Цель: ознакомиться и получить навык определения площадей графическим способом.

Площади участков, имеющих форму геометрических фигур треугольника, прямоугольника или трапеции, вычисляют по известным формулам геометрии [3,5]. Площадь треугольника 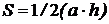, когда измерены основания 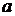и высота или 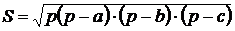, когда измерены стороны 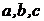и вычислен периметр 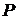. Площадь прямоугольника , где 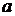– основание, высота, площадь трапеции , где – длины оснований, а – высота. Если участок представляет многоугольник, то его делят на элементарные геометрические фигуры – треугольники и трапеции.

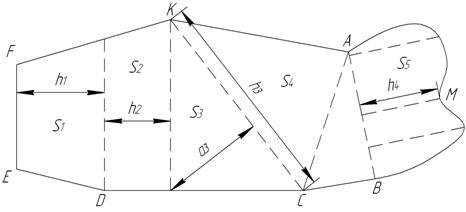
Рис. 2. Прямолинейная и криволинейная площадь

В каждой фигуре измеряют длины, по которым можно вычислить площадь. Иногда к сторонам многоугольника примыкают криволинейные контуры АМВ. В этих случаях перпендикуляры, опущенные из точек поворота на линию АВ, образуют трапеции и треугольники. Для вычисления площадей измеряют необходимые линии. Общая площадь многоугольника является суммой площадей отдельных фигур.

Точность определения площади графическим методом зависит от графической ошибки измерений линий плана. Известно, что линия плана определяется циркулем-измерителем с ошибкой 0,1 мм, которая не зависит от длины линии. Из этого следует, что относительная ошибка короткой линии больше, чем длинной. Поэтому при построении элементарных фигур надо стремиться к фигурам больших размеров и по возможности с одинаковыми длинами оснований и высот [3,5].

Для контроля и повышения точности площади можно определять дважды, для чего строят новые элементарные фигуры или в треугольниках измеряют другие основания и высоту. Относительное расхождение двухкратных определений общей площади не должно превышать точности 1/200 или 1–2 % по отношению к действительной площади.

Не нашли, что искали? Воспользуйтесь поиском: