
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Методы стохастического факторного анализа. Кореляционно-регрессионный анализ взаимосвязи между показателями
Стохастический анализ – это методика исследования факторов, связь которых с результативным показателем является вероятностной (корреляционной). При этом результативный признак (зависимая переменная) испытывает влияние не только рассматриваемых зависимых факторов, но и подвергается влиянию случайных (неконтролируемых) факторов. Причем полный перечень факторов не известен, так же, как и точный механизм их воздействия на результативный признак. Если при функциональной зависимости с изменением аргумента (фактора) происходит соответствующее изменение функции (результативного показателя), т. е. детерминированная зависимость проявляется в каждом случае, то при стохастической – изменение аргумента может повлечь за собой несколько значений функции. Таким образом, стохастическая связь проявляется не в каждом конкретном случае, а в среднем при большом числе наблюдений. Исходные данные при таком факторном анализе заданы выборкой, а результаты получают с некоторой вероятностью (надежностью), которую следует оценить.
Примером прямого стохастического факторного анализа служит:
– оценка влияния на товарооборот рациональности размещения торговой сети;
– оценка влияния на товарооборот покупательской способности населения (спроса, моды и т. д.);
– оценка зависимости динамики выручки от продажи товаров (или производительности труда) от изменения расходов на оплату труда;
– оценка зависимости товарооборота от расходов на рекламу и т. д.
Примером обратного стохастического факторного анализа служит комплексная оценка качества торгового обслуживания.
Задачи детерминированного факторного анализа (ДФА) нашли широкое применение в практике аналитической работы, однако детерминированный подход не позволяет учитывать влияние на результативный показатель очень многих факторов, не находящихся с ним в пропорциональной зависимости (спрос, текучесть кадров, размещение торговой сети и т. д.). Кроме того, в задачах ДФА невозможно выделить результаты одновременно действующих факторов. Эти недостатки обусловили необходимость применения стохастического моделирования в экономическом анализе, называемого иначе математико-статистическими методами изучения связей, которые являются в определенной степени дополнением и углублением ДФА.
Таким образом, в экономическом анализе стохастические модели используются в тех случаях, когда необходимо:
– оценить влияние факторов, по которым нельзя построить жестко детерминированную модель;
– изучить и сравнить влияние факторов, которые нельзя включить в одну и ту же детерминированную модель;
– выделить и оценить влияние сложных факторов, которые не могут быть выражены одним определенным количественным показателем.
В отличие от детерминированного, стохастический подход для своей реализации требует выполнения следующего ряда предпосылок:
1. Качественной однородности совокупности, т. е. в пределах варьирования значений факторов не должно происходить качественного скачка в характере отражаемого явления.
2. Достаточной численности совокупности наблюдения, позволяющей с точностью и надежностью выявить имеющиеся закономерности (в теории статистики считается, что количество наблюдений должно в 6-8 раз превышать количество факторов).
3. Наличия методов, т. е. специального математического аппарата, позволяющего выявить тесноту связи между изучаемыми показателями и оценить величину влияния факторов на изменение результативного показателя.
В целом, стохастическое моделирование предназначено для решения трех задач:
1) установления факта наличия или отсутствия связи между изучаемыми признаками;
2) выявления причинных связей между изучаемыми показателями и количественное измерение действия факторов на результативный показатель;
3) прогнозирования неизвестных значений результативных показателей.
Проведение стохастического моделирования осуществляется по следующим этапам:
1) качественный анализ, подразумевающий постановку цели анализа, определение результативных и факторных признаков, отбор и отсев факторов;
2) количественный анализ, т. е. построение регрессионной модели (уравнения регрессии) и расчет параметров уравнений регрессии;
3) проверка адекватности модели, т. е. оценка точности (надежности) уравнения связи и правомерности его использования для практической цели.
Практическая реализация указанных этапов основывается на применении корреляционного и регрессионного методов анализа.
Явления общественной жизни формируются под влиянием многочисленных и взаимосвязанных факторов, количественное выражение которых можно установить на основе качественного анализа при выявлении функциональной (полной) или корреляционной (неполной) связи.
При функциональной зависимости изменение результативного признака у всецело обусловлено действием факторного признака х, т.е. у = f(x).
При корреляционной зависимости изменение результативного признака у не полностью обусловлено влиянием факторного признака х, а лишь частично. Это происходит из-за того, что возможно влияние на результативность признаков и других факторов e: у = j(х)+ e.
Изучение связи между признаками методом корреляции используется в тех случаях, когда невозможно устранить посторонние факторы, либо потому, что эти факторы не известны, либо из-за невозможности их изоляции.
Различают следующие виды корреляционной связи.
В зависимости от количества взаимодействующих признаков: однофакторные – имеют место, когда исследуется связь между одним признаком-следствием у и одним признаком–фактором х (у = 5х наблюдается парная корреляция) и многофакторные связи–имеют место, когда исследуется влияние многих взаимодействующих между признаков-факторов на признак-следствие.
В зависимости от направленности корреляции связи бывают прямыми, когда зависимая переменная растет с увеличением факторного признака, и обратными, при которых рост последнего сопровождается уменьшением признака-результата (у = 5/ х). Относительно своей аналитической формы связи бывают линейными и нелинейными (прямолинейные и криволинейные). В первом случае между признаками проявляются линейные соотношения. Это происходит тогда, когда с увеличением значения признака–фактора происходит возрастание или уменьшение величины признака –следствия.
По силе взаимодействия корреляционные связи могут быть слабыми и сильными.
Корреляция – зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
В связи с этим при изучении корреляционных связей ставится задача установления количественных оценок степеней тесноты связи между признаками, а также установлением характера и направления этой зависимости.
Для решения этой задачи применяются две группы методов, включающие в себя методы корреляционного анализа и регрессионного анализа.
Корреляционно-регрессионный анализ как общее понятие включает в себя измерение тесноты, направления связи и установление аналитического выражения (формы) связи (регрессионный анализ).
В основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических данных уi от выравненных уxi.
Корреляционный метод позволяет количественно выразить взаимосвязь между показателями. При этом, если показатель зависит от одного фактора, то речь идет о парной корреляции, если же от множества факторов – то о множественной корреляции. Основная особенность корреляционного анализа состоит в том, что он устанавливает лишь факт наличия связи и степень ее тесноты, не вскрывая причины.
Задача корреляционного анализа – выявить тесноту связи изучаемых признаков, что осуществляется либо с помощью коэффициента корреляции (при прямолинейной зависимости), либо с помощью корреляционного отношения (при линейной и нелинейной зависимости).
Коэффициент корреляции (парный коэффициент корреляции, линейный коэффициент корреляции) между фактором х и результативным показателем Y определяется следующим образом:
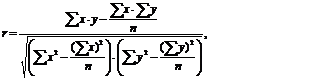
где y – абсолютное значение результативного показателя;
x – абсолютное значение фактора;
n – количество наблюдений.
Коэффициент корреляции может принимать значения от –1 до +1. При этом если:
Если r = -1, то это означает наличие функциональной связи обратно-пропорционального характера;
Если r = +1, то это означает наличие функциональной связи прямо-пропорционального характера (и в этом и в другом случае переходят к детерминированному факторному анализу);
Если r = 0, то это означает отсутствие связи между фактором и изучаемым результативным показателем (фактор исключается из факторной системы).
Другие значения r свидетельствуют о наличии стохастической зависимости, причем чем больше  стремится к 1, тем связь теснее. В частности:
стремится к 1, тем связь теснее. В частности:
 < 0,3 означает слабую связь;
< 0,3 означает слабую связь;
0,3 <  < 0,7 – связь средней тесноты;
< 0,7 – связь средней тесноты;
 > 0,7 – связь тесная, т.е. имеется объективная возможность перейти к стохастическому факторному анализу.
> 0,7 – связь тесная, т.е. имеется объективная возможность перейти к стохастическому факторному анализу.
При парной корреляции теснота связи изучается между результативным признаком и фактором.
В случае множественной корреляции тесноту связи между результативным показателем и набором факторов изучают на основе коэффициента множественной корреляции (R):
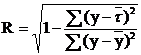 ,
,
где  – среднее значение результативного показателя, вычисленное по уравнению регрессии;
– среднее значение результативного показателя, вычисленное по уравнению регрессии;
 – среднее значение результативного показателя, вычисленное по исходным данным.
– среднее значение результативного показателя, вычисленное по исходным данным.
Коэффициент множественной корреляции принимает только положительные значения в пределах от 0 до 1. При значении R ≤ 0,3 говорят о малой зависимости между величинами, при значении 0,3 < R < 0,6 – о средней тесноте связи, при R > 0,6 – о наличии существенной связи.
При множественной корреляции теснота связи изучается:
– между результативным признаком (функцией) и каждой переменной (аргументом);
– между переменными попарно.
Альтернативным показателем степени зависимости между двумя переменными является коэффициент детерминации, представляющий собой возведение в квадрат коэффициента корреляции (r2 или R2 – величина достоверности аппроксимации). Коэффициент детерминации, значение которого должно стремиться к 1, показывает, чему равна доля влияния изучаемого (изучаемых) фактора (факторов) на результативный показатель. При этом следует помнить, что при условии, если r 2 (или R 2) < 0,5, синтезированные математические модели связи практического значения не имеют.
Практическая реализация корреляционного анализа включает следующие последовательные этапы:
1) постановка задач и выбор признаков;
2) формирование массива исходной статистической информации, определение степени ее однородности (на основе коэффициента вариации);
3) предварительная характеристика взаимосвязи (аналитические группировки, графики);
4) устранение мультиколлинеарности (взаимозависимости факторов), уточнение набора факторов (отбор наиболее существенных) на основе коэффициента корреляции, индекса детерминации или критерия Стьюдента. При этом в ходе отбора факторов следует придерживаться следующих правил:
– учитывать причинно-следственные связи между показателями (не рекомендуется включать в модель взаимосвязанные факторы: если парный коэффициент корреляции между двумя факторами больше 0,85, то один из них необходимо исключить).
– отбирать самые значимые факторы;
– рассматривать только те факторы, которые должны быть количественно измеримы, т. е. имеют единицу измерения и находить отражение в учете и отчетности;
– учитывать только однонаправленные факторы (т. е. при линейном характере зависимости нельзя включать в модель факторы, связь которых с результативным показателем имеет криволинейный характер);
После осуществления всех вышеуказанных процедур в случае установления факта высокой тесноты связи (> 0,7) приступают к решению второй задачи – регрессионному анализу, который позволяет выявить конкретные величины влияния факторов на изменение результативного показателя.
Регрессионный анализ – это метод установления аналитического выражения (т.е. уравнения регрессии) стохастической зависимости между исследуемыми признаками.
Уравнение регрессии показывает, как в среднем изменяется результативный признак (Y) при изменении любой из переменных (Х i) и имеет вид:
Y = f (x1,x2,…xn),
где Y – зависимая переменная, т.е. результативный показатель;
xi – независимые переменные (факторы).
В ходе регрессионного анализа решаются две главные задачи:
– построение уравнения регрессии, т. е. нахождение вида зависимости между результативным показателем и независимыми факторами;
– оценка значимости полученного уравнения (на основе коэффициента детерминации, критерия Фишера и критерия Стьюдента).
Вид уравнения регрессии определяется по графику, изображающему связь между факторами и результативным показателем, который строится на основе однородной совокупности статистических данных и служит обоснованием уравнения связи.
Если зависимость линейная (на графике изображена в виде прямой восходящей или снисходящей линии), то при:
а) однофакторном анализе уравнение будет иметь вид:
Y(х) = а +b·x,
где Y – результативный показатель;
b – коэффициент регрессии, который показывает, насколько изменится результативный показатель при изменении фактора на 1 ед.;
а – свободный член, который показывает величину влияния неучтенных факторов;
х – фактор;
б) многофакторном анализе уравнение будет иметь вид:
Y(х) = а +b1x1 + b2x2 +…+ bnxn.
Если зависимость нелинейная (на графике изображена в виде параболы или гиперболы), то уравнение регрессии принимает следующий вид:
– при графике в виде параболы
Y(х) = а +b·x + с·x2 ,
– при графике в виде гиперболы
Y(х) = а +b:x 2.
При сложном характере зависимости между изучаемыми явлениями используются более сложные параболы (третьего, четвертого порядка (полинома) и т. д.), а также квадратическое, степенные, показательные и другие функции.
Выбор конкретного уравнения регрессии и его решение осуществляется в рамках табличного процессора MS Excel или статистического программного пакета STADIA.
Сущность решения уравнений регрессии заключается в нахождении параметров регрессии (а и b). Это осуществляется по способу наименьших квадратов с использованием системы нормальных уравнений, суть которого заключается в минимизации суммы квадратов отклонений фактических значений результативного показателя от его расчетных значений.
При прямолинейной зависимости система нормальных уравнений имеет вид:
 |
∑y = na +b∑x,
∑xy = a∑x +b∑x2.
При криволинейной зависимости:
 |
∑ y=nf+b∑1/x
∑y(1/x)= a∑1/x +b∑(1/x)2.
Для оценки адекватности модели используют такие критерии, как ошибка аппроксимации, F-отношения, коэффициента детерминации.
В необходимых случаях построение уравнения регрессии может быть использовано для прогнозирования результативного признака.
Апробируем методику корреляционно-регрессионного анализа на конкретном примере.
Пример 1. На основании данных таблицы 1 необходимо проанализировать зависимость между расходами на оплату труда (Y) и выручкой от продажи товаров (х).
Таблица 1
Данные о выручке от продажи товаров и сумме расходов на оплату труда
в разрезе торговых организаций
В тыс. руб.
| № мага-зинов | Выручка от продажи товаров | Сумма расходов на оплату труда | № магазинов | Выручка от продажи товаров | Сумма расходов на оплату труда |
| 3 200 | 1 690 | ||||
| 7 450 | |||||
| 12 000 | 12 900 | ||||
| 8 560 | 2 010 | ||||
| 14 100 | 1 650 | ||||
| 11 300 | 5 115 | ||||
| 4 300 | 8 945 | ||||
| 1 010 | 11 900 | ||||
| 8 230 | 14 200 | ||||
| 12 560 | 10 300 | ||||
| 6 201 | 11 450 | ||||
| 11 500 | 13 000 | ||||
| 13 300 | 6 100 | ||||
| 1 000 | 7 500 |
На основании данных таблицы 1 построим график зависимости изменения расходов на оплату труда от изменения товарооборота (рисунок 1).

Рисунок 1 – Зависимость динамики расходов на оплату труда от выручки от продажи товаров
Данные графика свидетельствуют о том, что между расходами на оплату труда и выручкой от продажи товаров существует прямолинейная зависимость. Далее измерим тесноту связи между изучаемыми показателями на основе коэффициента корреляции, для чего сгруппируем магазины по сумме выручки от продажи товаров и составим следующую разработочную таблицу (таблица 2).
Таблица 2
Разработочная таблица для определения показателей, используемых при расчете коэффициента корреляции
| Группы магазинов по сумме выручки от продажи товаров | Количество магазинов | Выручка от продажи товаров (xi), млн. руб. | Сумма расходов на оплату труда (yi), млн. руб. | yi xi | xi2 | yi2 |
| От 500 до 3 220 включ. | 7,000 | 11,060 | 0,876 | 9,689 | 122,324 | 0,768 |
| От 3 221 до 5 440 включ. | 2,000 | 9,415 | 0,435 | 4,096 | 88,642 | 0,190 |
| От 5 441 до 8 160 включ. | 4,000 | 27,251 | 0,904 | 24,635 | 742,617 | 0,818 |
| От 8 161 до 10 880 включ. | 4,000 | 36,035 | 1,565 | 56,394 | 1298,521 | 2,450 |
| Св. 10 881 | 11,000 | 138,210 | 5,859 | 809,772 | 19102,004 | 34,328 |
| Итого | 28,000 | 221,971 | 9,639 | 904,586 | 21354,107 | 38,550 |
Согласно данным таблицы, элементы расчета коэффициента корреляции имеют следующие значения:
Уxi = 221,971;
Уyi = 9,639; Уyixi = 904,586; Уx2i = 21 354,107; Уy2 = 38,550.
Рассчитанные данные подставляются в формулу коэффициента корреляции:
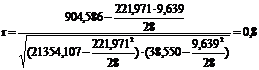
Коэффициент детерминации: r2 = 0,82 = 0,64.
Коэффициент корреляции, равный 0,8 ед., означает наличие высокой стохастической зависимости между суммой расходов на оплату труда и выручкой от реализации. Образование данной стохастической зависимости объясняется наличием (и доминированием в данном случае) постоянной части расходов по заработной плате, начисление которой не увязано с динамикой результата хозяйственной деятельности организации, т. е. выручки от продажи, а значение коэффициента детерминации, составляющее 0,64 ед. означает, что изменение расходов на оплату труда на 64 % объясняется изменением выручки от продажи, что дает основание для проведения регрессионного анализа.
Согласно виду графика, представленного на рисунке 1, между изучаемыми показателями существует прямолинейная корреляционная зависимость, в связи с чем уравнение регрессии будет иметь вид: Y(х) = а + b·x,
где Y – расходы на оплату труда; х – выручка от продажи товаров.
Для определения параметров а и в следует решить систему нормальных уравнений методом наименьших квадратов:
Отсюда значения коэффициента в определяется по формуле
 .
.
Рассчитанное значение параметра в говорит о том, что при увеличении выручки от продажи товаров на 1 млн. руб. расходы на оплату труда возрастут на 42,3 тыс. руб. При этом подставив значение данного параметра в первое уравнение системы, определим значение параметра а:
∑ y = na + b ∑ x;
9,639=а·28+0,0423·221,971;
28а=0,0423·221,971-9,639;
28а=0,2496;
а=0,009.
Значение параметра а показывает, что коэффициент регрессии может быть применим для торговых организаций с размером выручки от продажи за год свыше 9 млн. руб.
В целом уравнение регрессии имеет вид: y = 0,009+0,0423·х.
Полученное уравнение связи можно использовать для прогнозирования суммы расходов на оплату труда, если выручка от продажи возрастет и составит, например, 15 млн. руб.:
y = 0,009+0,0423· х =0,009+0,0423·15=0,644 млн. руб.
При выполнении регрессионного анализа необходимо получить оценки, позволяющие оценить точность модели, вероятность ее существования и обоснованность применения в аналитических целях. Таким образом, качество корреляционно-регрессионного анализа обеспечивается выполнением ряда следующих условий:
1. Однородность исходной информации, которая оценивается в зависимости от относительного ее распределения около среднего значения. Критериями здесь служат:
– среднеквадратическое отклонение;
– коэффициент вариации;
– коэффициент равномерности;
– закон нормального распределения.
2. Значимость коэффициентов корреляции может быть оценена (наряду с уже указанным выше коэффициентом детерминации) с помощью t- критерия Стьюдента, алгоритм расчета которого при линейной однофакторной связи имеет вид:
 .
.
Если полученное эмпирическое (расчетное) значение критерия (t э) будет больше критического табличного значения (t т), то коэффициент корреляции можно признать значимым.
3. Адекватность (надежность) уравнения регрессииоценивается с помощью F- критерия Фишера, алгоритм расчета которого выглядит следующим образом:
 ,
,
где m – число параметров уравнения регрессии;
σ2y – дисперсия по линии регрессии;
σ2ост – остаточная дисперсия.
Если эмпирическое значение F –критерия (F э) окажется выше табличного (F т), то уравнение регрессии следует признать адекватным, т.е. правомерным для использования. При этом чем выше величина критерия Фишера, тем точнее в уравнении связи представлена зависимость, сложившаяся между факторными и результативными показателями.
4. Сравнительной силой влияния факторов, оценка которой необходима с целью определения проблемной и наиболее эффективной в перспективе зоны для направления усилий в конкретную область бизнеса. Решение этой задачи может быть осуществимо посредством использования:
а) частных коэффициентов эластичности (Э i), показывающих ожидаемый рост результативного показателя (в %) с возрастанием факторного на 1 %:
 ,
,
б) стандартизированных бета-коэффициентов (в i):
 .
.
Чем выше бета-коэффициент, тем сильнее воздействие анализируемого фактора на результативный признак.
Не нашли, что искали? Воспользуйтесь поиском: