Мкость простых конденсаторов

Емкость конденсаторов простой формы можно вычислить. Для этого предполагают, что на каждой из обкладок находиться некоторый заряд q, и вычисляют потенциал в электрическом поле рассматриваемого конденсатора U(x,y,z). Если удается решить эту задачу, то отсюда получается и значение напряжения между обкладками конденсатора U. После этого емкость можно найти по формуле .

Ёмкость плоского конденсатора.

Будем считать, что зазор между пластинами мал по сравнению с их размерами, так что краевыми эффектами можно пренебречь. Если на единице поверхности обкладок имеется заряд σ и диэлектриком является вакуум, то полное напряжение между обкладками можно определить из распределения потенциала в поле плоского конденсатора

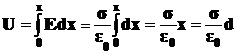, то ,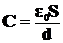

S – площадь каждой из пластин или меньшей из них, d – расстояние между пластинами. Полный заряд пластины . Если диэлектриком является не вакуум, а вещество с диэлектрической проницаемостью ε, заполняющее все пространство, где имеется электрическое поле (пространство между обкладками), то емкость будет в ε раз больше:

.

Ёмкость плоского многопластинчатого конденсатора отличается от ёмкости плоского конденсатора заменой S на S (n-1), где n – число пластин (обкладок).

.

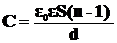При уменьшении расстояния d между обкладками ёмкость увеличивается.

Ёмкость цилиндрического конденсатора и коаксиального кабеля:

Пусть конденсатор состоит из двух коаксиальных цилиндров с радиусами r₂ (внешний) и r₁ (внутренний). Длину цилиндра будем считать весьма большой по сравнению с зазором между ними. Напряжение между обкладками

,

где r₂ и r₁ – радиусы внешнего и внутреннего цилиндров, l – длина цилиндра, q – заряд внутреннего цилиндра на единицу его длины.

Поэтому ёмкость цилиндрического конденсатора в вакууме

,

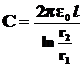Эта формула выражает, в частности, ёмкость кабеля, который состоит из металлического провода, окруженного слоем изолятора и металлической броней; данное выражение следует умножить еще на диэлектрическую проницаемость вещества изолятора

Ёмкость сферического конденсатора:

Если на обкладках конденсатора имеется заряд q, то напряжение между обкладками в вакууме

,

где r₂ и r₁ – радиусы внешней и внутренней сфер. Если диэлектриком является не вакуум, а вещество с диэлектрической проницаемостью ε, то

.

Если внешний радиус r₂ гораздо больше внутреннего r₁, то эта формула упрощается

Емкость двухпроводной линии:

Рассмотрим два параллельных цилиндрических провода с радиусами r и расстоянием между осями d (рис.5). Будем считать, что все остальные тела, включая и землю, находятся на расстояниях, больших по сравнению с d, и поэтому будем рассматривать оба провода как простой конденсатор. Предположим, что d >> a. В этом случае оба цилиндра заряжены равномерно. Так как напряжение в электростатическом поле не зависит от формы пути, то для его вычисления выберем простейший путь в виде прямой линии, соединяющей оси проводов и перпендикулярной к их поверхности. Поэтому напряжение U между проводами

,

Ёмкость двух проводной линии в вакууме

,

в диэлектрике

d – расстояние между осями проводов, r – радиус проводов, l – длина линии.

Для всех типов конденсаторов существует пробивное напряжение – разность потенциалов между обкладками, при которой происходит электрический разряд через слой диэлектрика. Пробивное напряжение зависит от толщины диэлектрика, его свойств и формы обкладок. С уменьшением толщины диэлектрика падает пробивное напряжение и при толщине 1 мкм пробивное напряжение не превышает 10 В. Увеличение емкости, при уменьшении толщины диэлектрика, происходит за счет снижения рабочего напряжения.

Не нашли, что искали? Воспользуйтесь поиском: