Измерение емкости и индуктивности

Рассмотрим основные методы измерения сосредоточенных постоян­ных – L и С, между токами и напряжениями в которых существуют из­вестные соотношения:

для С: или ; для L: или .

Метод амперметра - вольтметра наиболее простой метод измерения сосредоточенных постоян­ных. Сначала рассмотрим его работу на примере измерения активного со­противления R_х. Два варианта построения измерительных схем показаны на рисунке.

Сравнивая два варианта реализации метода амперметра-вольтметра и соответствующие им формулы для расчета измеряемого сопротивления, можно сделать вывод, что вариант а следует применять для определения сравнительно низкоомных сопротивлений, для которых выполняется соот­ношение (1), а вариант б, наоборот, для измерения сравнительно высокоомных сопро­тивлений, т.е. 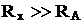(2).

Здесь R_A и R_B внутренние сопротивления амперметра и вольтметра соот­ветственно.

Метод амперметра-вольтметра используется и для измерения емко­сти С и индуктивности L. Для этого измерения проводят на переменном токе, задавая , затем определяют реактивные сопротивления X_C или Х_L и по формулам рассчитывают измеряемые величины: , .

Частота питающего напряжения f выбирается исходя из диапазона измеряемых значений С и L таким образом, чтобы их реактивные сопро­тивления Х_C и Х_L удовлетворяли неравенствам (1) или (2).

Метод амперметра-вольтметра широко применяется для построения простейших измерительных приборов – тестеров, пробников, авометров – как аналогового, так и цифрового типов. В цифровых приборах происходит преобразование тока и напряжения в цифровой код, и вычислительное устройство определяет величину измеряемого элемента путем расчета. Точность метода амперметра-вольтметра обычно составляет 5-10%.

Для более точных измерений используется мостовой метод.

При исследовании на переменном токе, мост может измерять как ак­тивное, так и реактивное сопротивления. Обычно условие равновесия мос­та, содержащее комплексные сопротивления , заменяют двумя усло­виями: для модулей комплексных сопротивлений (баланс амплитуд):

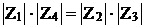, (17)

. (18)

Для балансировки моста на переменном токе необходимо подстраи­вать как минимум один активный и один реактивный элементы схемы, до­биваясь и баланса фаз, и баланса амплитуд. Обычно применяют мостовые схемы с двумя комплексными и двумя активными плечами. При этом воз­можны два варианта. В первом Z₁ и Z₂ – комплексные, а Z₃ и Z₄ – чисто ак­тивные:

, ; (19)

, .

и условие баланса фаз запишется по-другому:

. (20)

Анализируя оба варианта включения комплексных сопротивлений, можно заключить, что в первом уравновесить мост можно однородными реактивностями (обе С или обе L), а во втором — разнородными реактивностями (в одном плече С, а в другом L). Эту особенность мостовых пробо­ров необходимо учитывать при измерении индуктивностей и емкостей, поскольку в качестве набора образцовых реактивностей обычно применя­ются магазины конденсаторов.

Рисунок 7 – Схема моста при измерении емкости (а) и индуктивности (б)

Резонансный метод используется на частотах выше 1 МГц, где ба­лансировка мостовых схем затруднена из-за паразитных L и С элементов. В основу метода положено измерение резонансной характеристики коле­бательного контура, составленного из образцовой индуктивности L и из­меряемой емкости С, или наоборот. Во время измерений изменяется частота генератора синусоидальных колебаний Г, а его амплитуда остается постоянной. Напряжение с выхода генератора поступает на колебательный контур и вызывает в нём вынуж­денные колебания. С приближением к резонансу амплитуда вынужденных колебаний возрастает, и вольтметр В фиксирует максимальное напряже­ние. Максимум амплитуды А соответствует резонансной частоте колеба­тельного контура f_.0, которая отсчитывается по шкале генератора (рисунок 8, б). Зная один из элементов контура и его резонансную частоту, можно определить второй элемент колебательного контура. Из известной формулы

, (21)

находим измеряемые величины

, (22)

. (23)

Не нашли, что искали? Воспользуйтесь поиском: