ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ. · Напряженность E и потенциал φ поля точечного заряда q:

· Напряженность E и потенциал φ поля точечного заряда q:

, .

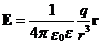· Связь между напряженностью и потенциалом поля:

,

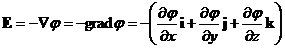где i, j, k – единичные орты декартовых координатных осей.

· Электрический момент диполя (дипольный момент):

p = |q| l,

где l – плечо диполя.

· Напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью

,

где n – нормаль к плоскости.

· Напряженность поля, создаваемого равномерно заряженной сферой радиуса R с зарядом q на расстоянии r от центра сферы:

E = 0, при r < R (внутри сферы),

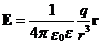, при r ≥ R (вне сферы).

· Напряженность поля, создаваемого объемно заряженным шаром радиуса R с зарядом q на расстоянии r от центра шара:

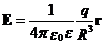, при r < R (внутри шара),

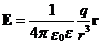, при r ≥ R (вне шара).

· Напряженность поля, создаваемого равномерно заряжен­ным бесконечным цилиндром радиуса R на расстоянии r от оси цилиндра:

E = 0, при r < R (внутри цилиндра),

, при r ≥ R (вне цилиндра).

· Работа, совершаемая силами электростатического поля при перемещении заряда q из точки 1 в точку 2:

A ₁₂ = q (φ ₁ – φ ₂) или .

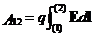· Напряженность электрического поля у поверхности проводника:

E_n = ,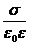

где σ поверхностная плотность зарядов.

· Поляризованность:

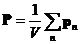
где V – объем диэлектрика; p _n – дипольный момент n -ой молекулы.

· Поток поляризованности P через замкнутую поверхность S:

,

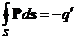где 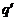- алгебраическая сумма связанных зарядов внутри этой поверхности

· Вектор D и теорема Гаусса для него:

D = ε ₀ E + P, ,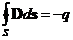

где q – алгебраическая сумма сторонних зарядов внутри замкнутой поверхности.

· Условия на границе раздела двух диэлектриков:

P _{2 n} – P _{1 n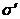} = - , D _{2 n} - D _1n = σ, E _{2 τ} = E _{1 τ} ,

где 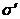и σ – поверхностные плотности связанных и сторонних зарядов, а орт нормали n направлен из среды 1 в среду 2.

· Для изотропных диэлектриков:

P = κε E, D = ε ₀ ε E, ε = 1 + κ.

· Электроемкость уединенного проводника:

C = ,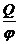

где Q – заряд, сообщенный проводнику; φ – потенциал проводника.

· Емкость плоского конденсатора:

C = ,

где S – площадь каждой пластины конденсатора; d – расстояние между пластинами.

· Емкость системы конденсаторов при последовательном и параллельном соединении:

, ,

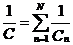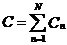где C_n – емкость n -го конденсатора; N – число конденсаторов.

· Энергия уединенного заряженного проводника:

.

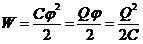· Энергия взаимодействия системы точечных зарядов:

,

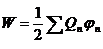где φ_n – потенциал, создаваемый всеми зарядами, кроме n -го, в той точке, где находится заряд Q _n.

· Энергия заряженного конденсатора:

,

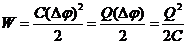где Q – заряд конденсатора; C – его емкость; Δ φ – разность потенциалов между обкладками.

· Объемная плотность энергии:

.

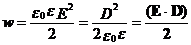Не нашли, что искали? Воспользуйтесь поиском: