
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. 1. Точечный заряд удалили от точки А на расстояние, в N =3 раза превышающее первоначальное
1. Точечный заряд удалили от точки А на расстояние, в N =3 раза превышающее первоначальное. Во сколько раз уменьшится напряженность электрического поля в точке А?
Решение: Напряженность электрического поля вначале E 1 = kQ / r 12, где k = 9*109 Н∙м2/Кл2, а Q – величина заряда, r 1 – начальное расстояние от точки А до точечного заряда; а в конце – E 2 = kQ / r 22, где r 2 = Nr 1 - конечное расстояние от точки А до заряда. Разделив Е 1 на Е 2, получаем Е 1/ Е 2 = (r 2/ r 1)2 = N 2 = 9.
2. Частица, имеющая заряд q, разгоняется до энергии W и влетает в плоский конденсатор параллельно его пластинам. Заряд конденсатора Q, его емкость C, расстояние между пластинами d. Первоначально частица находится на одинаковом расстоянии от пластин. Какой длины l должны быть каждая пластина, чтобы частица не упала на ее поверхность?
Решение: Пусть m – масса частицы, тогда ее скорость 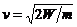 . Напряжение на обкладках конденсатора U = Q/C, а напряженность поля внутри конденсатора E = U/d = Q/Cd. Ускорение, с которым частица будет двигаться к одной из обкладок a = EQ/m = Qq/Cdm. Время полета частицы в конденсаторе
. Напряжение на обкладках конденсатора U = Q/C, а напряженность поля внутри конденсатора E = U/d = Q/Cd. Ускорение, с которым частица будет двигаться к одной из обкладок a = EQ/m = Qq/Cdm. Время полета частицы в конденсаторе 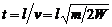 . За это время частица сместится с оси конденсатора на расстояние at 2/2 и не упадет на пластину, если это расстояние меньше d /2: d /2> at 2/2 → d > = Qql 2/2 CdW, откуда следует ответ:
. За это время частица сместится с оси конденсатора на расстояние at 2/2 и не упадет на пластину, если это расстояние меньше d /2: d /2> at 2/2 → d > = Qql 2/2 CdW, откуда следует ответ: 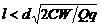
3. Плоский воздушный конденсатор емкостью C подключен к источнику тока с напряжением U. Какую работу A 1 необходимо совершить, чтобы вдвое увеличить расстояние между обкладками конденсатора? Какую работу A 2 совершает при этом источник?
Решение: После увеличения расстояния между обкладками конденсатора вдвое его емкость уменьшилась в два раза. Начальный заряд на обкладках q = CU, а конечный q’ = (CU)/ 2. По определению, работа источника A 2 = U ∆ q = U(q’ - q) = -(CU 2)/2. По закону сохранения энергии (q ’)2/(2 C’) – q 2/(2 C) = A 1 + A 2. Подставляя в это уравнение q ’ = q /2, C ’ = C /2 и выражение для A 2, находим A 1 = (CU 2)/4.
ЗАДАЧИ И УПРАЖНЕНИЯ [1]
Q.1. На некотором расстоянии друг от друга находятся два одинаковых по модулю точечных заряда A и B. Считая напряженность поля положительной в направлении, совпадающем с положительным направлением оси x, определить знаки зарядов для каждого из представленных на рисунках распределений напряженности поля между зарядами.
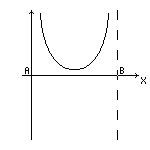 а) а)
| 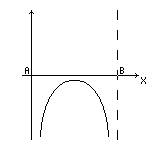 б) б)
|
 в) в)
| 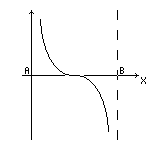 г) г)
|
Q.2. Два положительно заряженных тела с зарядами 1,67 и 3,34 нКл находятся на расстоянии 20 см друг от друга. В какой точке на линии, соединяющей эти тела, надо поместить третье тело с зарядом -0,67 нКл, чтобы оно оказалось в равновесии? Массами тел пренебречь.
●Q.3. Три отрицательных заряда по 9 нКл каждый расположены в вершинах равностороннего треугольника. Какой заряд нужно поместить в центре треугольника, чтобы система находилась в равновесии?
Q.4. Три заряда расположены в вершинах равнобедренного прямоугольного треугольника, причем у острых углов находятся заряды + Q и - Q, а у прямого угла – заряд +2 Q. Определить, какой из пронумерованных векторов совпадает с направлением напряженности поля в точке, находящейся на середине гипотенузы.
 Q.5. В трех вершинах квадрата со стороной 40 см находятся оди-наковые положительные заряды по 5 нКл каждый. Найти напряженность поля в четвертой вершине.
Q.5. В трех вершинах квадрата со стороной 40 см находятся оди-наковые положительные заряды по 5 нКл каждый. Найти напряженность поля в четвертой вершине.
Q.6. Легкий бузиновый шарик, подвешенный на шелковой нити, притягивается палочкой. Значит ли это, что палочка была первоначально наэлектризована? А если бузиновый шарик от палочки отталкивается?
Q.7. Два точечных заряда: отрицательный - q с массой m и положительный Q с массой M расположены на расстоянии l друг от друга. Какой должна быть напряженность E внешнего электрического поля, чтобы заряды двигались с одинаковым ускорением a? Чему равно это ускорение?
●Q.8. Определить поток ΦЕ вектора напряженности электростатического поля через сферическую поверхность, охватывающую точечные заряды Q 1 = 5 нКл и Q 2 = -2 нКл.
●Q.9. Определить напряженность поля, создаваемого диполем с электрическим моментом p = 10-9 Кл∙м на расстоянии r = 25 см от центра диполя в направлении, перпендикулярном его оси.
●Q.10. Кольцо радиусом r = 5 см из тонкой проволоки равномерно заряжено с линейной плотностью λ = 14 нКл/м. Определить напряженность поля на оси, проходящей через центр кольца, в точке A, удаленной на расстояние a = 10 см от плоскости кольца.
●Q.11. Электростатическое поле создается двумя бесконечными параллельными плоскостями, равномерно заряженными одноименными зарядами с поверхностной плотностью соответственно σ 1 = 2 нКл/м2 и σ 2 = 4 нКл/м2. Определить напряженность электростатического поля: 1) между плоскостями; 2) за пределами плоскостей. Построить график изменения напряженности поля вдоль линии, перпендикулярной плоскостям.
●Q.12. Поле создано двумя равномерно заряженными концентрическими сферами с радиусами R 1 = 5 см и R 5 = 8 см. Заряды сфер соответственно равны Q 1 = 2 нКл и Q 5 =-1 нКл. Определить напряженность электрического поля в точках, лежащих от центра сфер на расстояниях: 1) r 1 = 3 см; 2) r 2 = 6 см; 3) r 3 = 10 см. Построить график зависимости E (r).
Q.13. По первоначальным представлениям Н. Бора электрон в атоме водорода движется по круговой орбите. Вычислить скорость движения электрона, если радиус его орбиты 0,5∙10-8 см.
 Q.14. Два точечных заряда 6,7 и -13,4 нКл находятся на расстоянии 5 см друг от друга. Найти напряженность электрического поля в точке, расположенной на расстоянии 3 см от положительного заряда и 4 см от отрицательного.
Q.14. Два точечных заряда 6,7 и -13,4 нКл находятся на расстоянии 5 см друг от друга. Найти напряженность электрического поля в точке, расположенной на расстоянии 3 см от положительного заряда и 4 см от отрицательного.
Q.15. Поле создано бесконечной вертикальной плоскостью с поверхностной плотностью заряда σ = 4 нКл/см2, к которой подвешен на нити шарик массой 1 г и зарядом 1 нКл. Определить угол, образованный нитью и плоскостью.
Q.16. Два одинаково заряженных шарика, имеющие массу 0,5 г и подвешенные на нитях длиной по 1 м, разошлись на 4 см друг от друга. Найти заряд каждого шарика.
Q.17. Два одинаковых положительных заряда находятся на расстоянии l друг от друга. Найти на прямой, перпендикулярной линии, соединяющей заряды и проходящей через середину этой линии, точки, в которых напряженность поля максимальна.
●Q.18. Длинный прямой провод, расположенный в вакууме, несет заряд, равномерно распределенный по всей длине провода с линейной плотностью λ = 2 нКл/м. Определить напряженность E электростатического поля на расстоянии r = 1 м от провода.
●Q.19. Электростатическое поле создается положительно заряженной бесконечной нитью с постоянной линейной плотностью λ = 1 нКл/см. Какую скорость приобретет электрон, приблизившись под действием поля нити вдоль линии напряженности с расстояния r 1 = 1,5 см до r 2 = 1 см?
●Q.20. Кольцо радиусом r = 5 см из тонкой проволоки несет равномерно распределенный заряд Q =10 нКл. Определить потенциал φ электростатического поля: 1) в центре кольца; 2) на оси, проходящей через центр кольца, в точке, удаленной на расстояние a = 10 см от плоскости кольца.
Q.21. С какой силой (на единицу площади) отталкиваются две одноименно заряженные бесконечно протяженные плоскости с поверхностной плотностью заряда σ 1 = 3∙10-8 Кл/см2 и σ 2 = 6∙10-8 Кл/см2?
Q.22. Две длинные одноименно заряженные нити расположены на расстоянии a = 10 см друг от друга. Линейная плотность зарядов на нитях одинакова и 10-7 Кл/см. Найти величину и направление напряженности результирующего электрического поля в точке, находящейся на расстоянии 10 см от каждой нити.
Q.23. Тонкий стержень длиной 20 см равномерно заряжен с линейной плотностью заряда λ =1 нКл/см. Определить напряженность поля, созданного стержнем в точке A на продолжении его оси на расстоянии 10 см от ближнего конца, и силу взаимодействия стержня и заряда q =10-8 Кл, если его поместить в точку A.
Q.24. Найти напряженность поля E и его потенциал φ на оси тонкого равномерно заряженного кольца.
Q.25. Найти поле равномерно заряженного шара радиуса R, суммарный заряд которого равен Q.
●Q.26. Полый шар несет на себе равномерно распределенный заряд. Определить радиус шара, если потенциал φ 0 в центре шара равен 200 В, а в точке, лежащей от его центра на расстоянии r = 50 см, 40 В.
●Q.27. Электростатическое поле создается бесконечной прямой нитью, заряженной равномерно с линейной плотностью λ = 50 пКл/см. Определить числовое значение и направление градиента потенциала в точке на расстоянии r = 0,5 м от нити.
●Q.28. Электростатическое поле создается бесконечной плоскостью, равномерно заряженной с поверхностной плотностью σ = 1 нКл/м2. Определить разность потенциалов между двумя точками этого поля, лежащими на расстояниях x 1 = 20 см и x 2 = 50 см от плоскости.
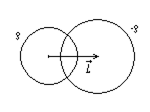 Q.29. Полубесконечная прямая, равномерно заряженная нить имеет заряд λ на единицу длины. Найти модуль и направление напряженности поля в точке, которая отстоит от нити на расстоянии y и находится на перпендикуляре к нити, проходящем через ее конец.
Q.29. Полубесконечная прямая, равномерно заряженная нить имеет заряд λ на единицу длины. Найти модуль и направление напряженности поля в точке, которая отстоит от нити на расстоянии y и находится на перпендикуляре к нити, проходящем через ее конец.
Q.30. Найти напряженность E электрического поля в области пересечения двух шаров, равномерно заряженных разноименными по знаку зарядами с объемной плотностью ρ и -ρ, если расстояние между центрами шаров определяется вектором l.
Q.31. Три точечных заряда Q 1, Q 2, Q 3 образуют электрически нейтральную систему, причем Q 1 = Q 2 = 10 нКл. Заряды расположены в вершинах равностороннего треугольника. Определить максимальные значения напряженности E max и потенциала φ max, создаваемого этой системой зарядов на расстоянии r = 1 м от центра треугольника, длина a стороны которого равна 10 см.
Q.32. Два шарика с зарядами 6,7 и 13,4 нКл находятся на расстоянии 40 см друг от друга. Какую минимальную работу нужно совершить, чтобы сблизить их до расстояния 25 см?
Q.33. Электрическое поле создано тонким стержнем, несущим равномерно распределенный по длине заряд с λ = 0,1 мкКл/м. Определить потенциал φ поля в точке, удаленной от концов стержня на расстояние, равное длине стержня.
●Q.34. Электростатическое поле создается сферой радиуса R = 5 см, равномерно заряженной с поверхностной плотностью σ = 1 нКл/м2. Определить разность потенциалов между двумя точками поля, лежащими на расстояниях r 1 = 10 см и r 2 = 15 см от центра сферы.
●Q.35. Электростатическое поле создается шаром радиусом R = 10 см, равномерно заряженным с объемной плотностью ρ = 20 нКл/м3. Определить разность потенциалов между точками, лежащими внутри шара на расстояниях r 1 =2 см и r 2 = 8 см от центра шара.
●Q.36. В однородное электростатическое поле напряженностью E 0 = 700 В/м перпендикулярно полю помещается бесконечная плоскопараллельная пластина (ε = 7). Определить: 1) напряженность электростатического поля внутри пластины; 2) электрическое смещение; 3) поляризованность стекла; 4) поверхностную плотность связанных зарядов на стекле.
Q.37. Электрическое поле создано длинным цилиндром радиуса R =1 см, равномерно заряженным с линейной плотностью λ =20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстояниях a 1 = 0,5 см и a 2 =2 см от поверхности цилиндра в средней его части.
Q.38. Определить начальную скорость v 0 сближения протонов, находящихся на достаточно большом расстоянии друг от друга, если минимальное расстояние r min, на которое они могут сблизиться, равно 10-11 см.
Q.39. Имеется бесконечная цепочка чередующихся зарядов q и - q. Расстояние между соседними зарядами равно a. Найти энергию взаимодействия каждого заряда со всеми остальными.
Q.40. Потенциал некоторого электрического поля имеет вид φ = α (xy – z 2). Найти проекцию вектора E на направление вектора a = i +3 k в точке M (2,1,-3).
Q.41. Напряженность электрического поля зависит только от координат x и y как E = a (x i + y j)/(x 2 + y 2), где a – постоянная, i и j – орты осей OX и OY. Найти заряд внутри сферы радиуса R с центром в начале координат.
Q.42. В атоме йода, находящемся на расстоянии r = 1 нм от α -частицы, индуцирован электрический момент p =1,5∙10-32 Кл∙м. Определить поляризуемость β атома йода.
Q.43. Всегда ли два одноименно, например, положительно, заряженных тела будут отталкиваться?
●Q.44. Между пластинами плоского конденсатора помещено два слоя диэлектрика – слюдяная пластинка (ε 1 = 7) толщиной d 1 =1 мм и парафин (ε 2 =2) толщиной d 2 = 0,5 мм. Определить: 1) напряженности электростатических полей в слоях диэлектрика; 2) электрическое смещение, если разность потенциалов между пластинами конденсатора U = 500 В.
●Q.45. Расстояние между пластинами плоского конденсатора d =5 мм, разность потенциалов U = 1,2 кВ. Определить: 1) поверхностную плотность заряда на пластинах конденсатора; 2) поверхностную плотность связанных зарядов на диэлектрике, если известно, что диэлектрическая восприимчивость диэлектрика, заполняющего пространство между пластинами χ = 1.
Q.46. К пластинам плоского воздушного конденсатора приложена разность потенциалов U 1 = 500 В. Площадь пластин S = 200 см2, расстояние между ними d = 1.5 мм. После отключения конденсатора от источника напряжения в пространство между пластинами внесли парафин (ε = 2). Определить разность потенциалов U 2 между пластинами после внесения диэлектрика. Определить также емкости конденсатора C 1 и C 2 до и после внесения диэлектрика.
●Q.47. Два взаимно перпендикулярных бесконечно длинных проводника, несущих равномерно распределенные зар-яды с ли 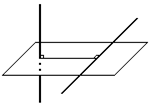 нейными плотностями λ 1 и λ 2, находятся на расстоянии a друг от друга. Как зависит кулоновская сила взаимодействия между проводниками от расстояния a?
нейными плотностями λ 1 и λ 2, находятся на расстоянии a друг от друга. Как зависит кулоновская сила взаимодействия между проводниками от расстояния a?
Q.48. Электрическое поле образовано положительно заряженной бесконечно длинной нитью. Двигаясь под действием этого поля от точки, находящейся на расстоянии x 1 = 1 см от нити, до точки x 2 = 4 см, α -частица изменила свою скорость от 2∙105 до 3∙106 м/с. Найти линейную плотность заряда на нити.
 Q.49. На некотором расстоянии a от бесконечно длинного прямолинейного проводника с равномерно распределенным линейным зарядом λ находится диполь с электрическим моментом p. Считая плечо диполя весьма малым по сравнению с расстоянием a, определить силу, действующую на диполь.
Q.49. На некотором расстоянии a от бесконечно длинного прямолинейного проводника с равномерно распределенным линейным зарядом λ находится диполь с электрическим моментом p. Считая плечо диполя весьма малым по сравнению с расстоянием a, определить силу, действующую на диполь.
Q.50. Два шарика одинакового радиуса в 1 см и массой по 4∙10-5 кг подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. Когда шарики зарядили, нити разошлись на некоторый угол и натяжение нитей стало равно T = 4,9∙10-4 H. Найти потенциал заряженных шариков, если известно, что расстояние от точки подвеса до центра каждого шарика равно 10 см.
Q.51. По тонкой нити, изогнутой по дуге окружности радиуса R, равномерно распределен заряд с линейной плотностью λ = 10 нКл/м. Определить напряженность E и потенциал φ электрического поля, создаваемого таким распределением заряда в точке O, совпадающей с центром кривизны. Длина l нити составляет 1/3 длины окружности и равна 15 см.
●Q.52. Определить напряженность электростатического поля на расстоянии d = 1 см от оси коаксиального кабеля, если радиус его центральной жилы r 1 = 0,5 см, а радиус оболочки r 2 = 1,5 см. Разность потенциалов между центральной жилой и оболочкой U = 1 кВ.
●Q.53. Два плоских воздушных конденсатора одинаковой емкости соединены параллельно и заряжены до разности потенциалов U = 300 В. Определить разность потенциалов этой системы, если пространство между пластинами одного из конденсаторов заполнить слюдой (ε = 7).
Q.54. Два заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в керосин плотностью 800 кг/м3. Какова должна быть плотность материала шариков, чтобы угол расхождения нитей на воздухе и в керосине был один и тот же. Диэлектрическая проницаемость керосина ε = 2.
Q.55. Внутренний цилиндрический проводник длинного прямого коаксиального провода радиусом R 1 = 1,5 мм заряжен с линейной плотностью λ 1 = 0,20 нКл/м. Внешний цилиндрический проводник этого провода радиусом R 2 =3 мм заряжен с линейной плотностью λ 2 = -0,15 нКл/м. Пространство между проводниками заполнено резиной (ε =3). Определить напряженность электростатического поля в точках, лежащих от оси провода на расстояниях: 1) r 1=1 мм; 2) r 2 = 2 мм; 3) r 3 = 5 мм.
Q.56. В однородное электростатическое поле напряженностью E 0 = 700 В/м перпендикулярно полю помещается бесконечная плоскопараллельная стеклянная пластинка (ε = 7). Определить: 1) напряженность электростатического поля внутри пластины; 2) электрическое смещение внутри пластины; 3) поверхностную плотность связанных зарядов на стекле.
Q.57. Свободные заряды равномерно распределены с объемной плотностью ρ =5 нКл/м3 по шару радиусом R = 10 см из однородного изотропного диэлектрика с проницаемостью ε = 5. Определить напряженность электростатического поля на расстояниях r 1 = 5 см и r 5 = 15 см от центра шара.
●Q.58. Сплошной эбонитовый шар (ε = 3) радиусом R = 5 см заряжен равномерно с объемной плотностью ρ = 10 нКл/м3. Определить энергию электростатического поля, заключенную внутри шара.
●Q.59. В однородное электростатическое поле напряженностью E 0 = 700 В/м перпендикулярно полю поместили стеклянную пластинку (ε =7) толщиной d = 1,5 мм и площадью S = 200 см2. Определить: 1) поверхностную плотность связанных зарядов на стекле; 2) энергию электростатического поля, сосредоточенную в пластинке.
●Q.60. Разность потенциалов между пластинами плоского конденсатора U = 100 В. Площадь каждой пластины S = 200 см2, расстояние между пластинами d = 0,5 мм, пространство между ними заполнено парафином (ε =2). Определить силу притяжения пластин друг к другу.
Q.61. Между обкладками плоского конденсатора, заряженного до разности потенциалов 1,5 кВ, зажата парафиновая пластинка (ε =2) толщиной 5 мм. Определить поверхностную плотность связанных зарядов на парафине.
Q.62. Точечный заряд q находится в вакууме на расстоянии l от плоской поверхности однородного диэлектрика, заполняющего все полупространство. Проницаемость диэлектрика ε. Найти: 1) Поверхностную плотность связанных зарядов как функцию расстояния r от точечного заряда q и исследовать полученный результат; 2) Суммарный связанный заряд на поверхности диэлектрика.
Q.63. Почему окраска небольших предметов методом разбрызгивания краски экономически выгодна, а также безвредна для здоровья работающего, если между пульверизатором и предметом создать высокое напряжение?
Q.64 Доказать, что при параллельном соединении конденсаторов
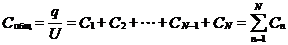 .
.
Q.65. Доказать, что при последовательном соединении конденсаторов
 .
.
Q.66. Найти емкость сферического конденсатора с радиусами R 1 < R 2, который заполнен изотропным диэлектриком с проницаемостью ε = a/r, где a – постоянная, r – расстояние от центра конденсатора.
Q.67. Найти емкость изображённой на рисунке батареи конденсаторов.
Q.68. 1000 одинаковых шарообразных капелек ртути заряжены до одного и того же потенциала φ 1 = 1 В. Каков будет потенциал φ большой капли, получившейся в результате слияния этих капель?
●Q.69. Определить емкость C батареи конденсаторов, изображенной на рисунке. Емкость каждого конденсатора C 1 = 1 мкФ.
 Q.70. Воздушный конденсатор емкостью C заполняют диэлектриком с диэлектрической проницаемостью ε. Какой конденсатор (какой емкости) надо включить последовательно с данным, чтобы такая батарея вновь имела емкость C?
Q.70. Воздушный конденсатор емкостью C заполняют диэлектриком с диэлектрической проницаемостью ε. Какой конденсатор (какой емкости) надо включить последовательно с данным, чтобы такая батарея вновь имела емкость C?
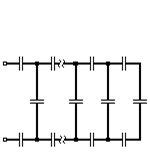 Q.71. Найти емкость бесконечной цепочки, составленной из одинаковых конденсаторов емкостью C.
Q.71. Найти емкость бесконечной цепочки, составленной из одинаковых конденсаторов емкостью C.
Q.72. Длинный прямой провод расположен параллельно безграничной проводящей плоскости. Радиус сечения провода равен a, расстояние между осью провода и проводящей плоскостью – h. Найти взаимную емкость этой системы на единицу длины провода при условии a << h.
 Q.73. Четыре одинаковые металлические пластины расположены в воздухе на одинаковом расстоянии d друг от друга. Площадь каждой пластины равна S. Найти емкость системы между точками A и B, если пластины соединены так, как показано на рисунке.
Q.73. Четыре одинаковые металлические пластины расположены в воздухе на одинаковом расстоянии d друг от друга. Площадь каждой пластины равна S. Найти емкость системы между точками A и B, если пластины соединены так, как показано на рисунке.
Q.74 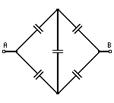 . Найти емкость CAB изображен-ной на рисунке батареи конденсаторов, ес-ли она включается в цепь точками A и B.
. Найти емкость CAB изображен-ной на рисунке батареи конденсаторов, ес-ли она включается в цепь точками A и B.
Q.75. Найти разность потенциалов  между точками A и B изображенной на рисунке схемы.
между точками A и B изображенной на рисунке схемы.
ПОСТОЯННЫЙ ТОК
Не нашли, что искали? Воспользуйтесь поиском: