
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
БИО - САВАРА - ЛАПЛАСА ЗАКОН
[по имени франц. учёных Ж. Б. Био (J. В. Biot; 1774 - 1862), Ф. Савара (F. Savart; 1791 - 1841) и П. С. Лапласа (P. S, Laplace; 1749 - 1827)] - один из основных законов магнитного поля тока. Согласно Б. - С. - Л. з. вектор dB индукции магн. поля, создаваемого в вакууме элементом d l проводника
 с током силой I, в произвольной точке М поля равев (см. рис.):
с током силой I, в произвольной точке М поля равев (см. рис.):
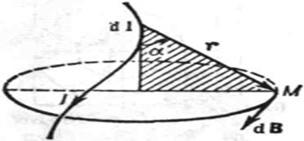 где dl - вектор, проведённый в направлении тока в элементе dl проводника, г - радиус-вектор, проведённый в точку М из элемента dl, r расстояние от dl до М, а. - угол между векторами dl и r, н0 - магнитная постоянная. Вектор dB перпендикулярен к dl и r и направлен так, что из конца dB вращение от dl к r по кратчайшему направлению видно происходящим против хода часовой стрелки (на рис. вектор dB направлен из-за чертежа).
где dl - вектор, проведённый в направлении тока в элементе dl проводника, г - радиус-вектор, проведённый в точку М из элемента dl, r расстояние от dl до М, а. - угол между векторами dl и r, н0 - магнитная постоянная. Вектор dB перпендикулярен к dl и r и направлен так, что из конца dB вращение от dl к r по кратчайшему направлению видно происходящим против хода часовой стрелки (на рис. вектор dB направлен из-за чертежа).
| Магнитное поле кругового тока | |
Рассмотрим поле, создаваемое током I, текущим по тонкому проводу, имеющему форму окружности радиуса R.
 Определим магнитную индукцию на оси проводника с током на расстоянии х от плоскости кругового тока. Векторы
Определим магнитную индукцию на оси проводника с током на расстоянии х от плоскости кругового тока. Векторы  перпендикулярны плоскостям, проходящим через соответствующие перпендикулярны плоскостям, проходящим через соответствующие 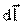 и и  . Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий вектор . Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий вектор  направлен вдоль оси кругового тока. Каждый из векторов направлен вдоль оси кругового тока. Каждый из векторов  вносит вклад равный вносит вклад равный  , а , а 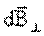 взаимно уничтожаются. Но взаимно уничтожаются. Но  , ,  , а т.к. угол между , а т.к. угол между 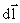 и и  α – прямой, то α – прямой, то  тогда получим тогда получим
Подставив в (1.6.1)
При
Заметим, что в числителе (1.6.2)
Силовые линии магнитного поля кругового тока хорошо видны в опыте с железными опилками (рис. 1.8).
Рис. 1.8 |
Не нашли, что искали? Воспользуйтесь поиском:
 ,
,
 и, проинтегрировав по всему контуру
и, проинтегрировав по всему контуру  , получим выражение для нахождения магнитной индукции круговоготока:
, получим выражение для нахождения магнитной индукции круговоготока: ,
,
 , получим магнитную индукцию в центре кругового тока:
, получим магнитную индукцию в центре кругового тока: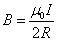 ,
,
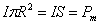 – магнитный момент контура. Тогда, на большом расстоянии от контура, при
– магнитный момент контура. Тогда, на большом расстоянии от контура, при  , магнитную индукцию можно рассчитать по формуле:
, магнитную индукцию можно рассчитать по формуле: ,
,

