Лабораторна робота № 17

Експериментальна перевірка співВідношення невизначенОСТей Гейзенберга для фотонів

Мета роботи

Експериментально перевірити співвідношення невизначеностей Гейзенберга для координати і відповідної їй проекції імпульсу фотонів

Для виконання лабораторної роботи студенту попередньо необхідно: знати фізичну суть співвідношень невизначеностей Гейзенберга для мікрочастинок (§4.3)

Прилади і обладнання

Гелій−неоновий лазер типу ЛГ–56, щілина з мікрометричним гвинтом, екран з міліметровою шкалою

Теоретичні відомості та опис установки

В даній лабораторній роботі пропонується перевірити експериментально співвідношення невизначеностей Гейзенберга для координати і відповідної проекції імпульсу фотонів, зокрема:

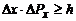. (1)

З врахуванням теоретичних викладок (див. §4.3) та згідно рис. 1, для малих кутів дифракції світла невизначеність проекції імпульсу фотонів на координату ОX можна записати наступним чином:

, (2)

де D – півширина центрального дифракційного максимуму, − відстань від щілини до екрана, 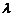− довжина хвилі монохроматичного випромінювання.

Підставивши (2) у формулу (1), отримаємо вираз:

. (3)

Цей вираз є робочою формулою для перевірки співвідношення невизначеності Гейзенберга для координати х і проекції імпульсу фотонів.

Схематично лабораторна установка зображена на рис. 1.

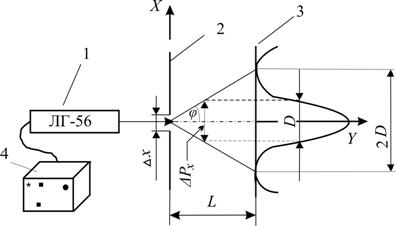
Рис.1

1 – He–Ne лазер типу ЛГ-56; 2 – розсувна щілина; 3 – екран; 4 - блок живлення лазера.

Лазер 1 встановлюють на краю оптичної лави. На протилежному кінці лави розташовують два рейтери: один з тримачем для щілини 2, другий – з тримачем для екрана 3. При освітленні лазерним променем щілини 2 на екрані 3 формується дифракційна картина.

При виконанні роботи слід виміряти ширину щілини, яка характеризує невизначеність координати фотона , а також півширину D центрального дифракційного максимуму, яка характеризує невизначеність імпульсу фотонів .

Послідовність виконання роботи

1. Зібрати установку згідно рис. 1. При цьому щілину 2 розмістити на відстані ~ 0,2 м від лазера 1. Екран 3 встановити на протилежному кінці оптичної лави. Відстань між щілиною та екраном встановити =1,5–2,0 м.
2. Увімкнути блок живлення лазера в мережу 220 В. Після ~ 5 хв натиснути на блоці живлення кнопку “Випромінювання”. При цьому появиться лазерний промінь. УВАГА! Із-за використання високої напруги в лазері (до 5000 В) слід бути гранично уважним при виконанні роботи: така напруга небезпечна для життя.
3. Отримати чітку дифракційну картину на екрані 3.
4. За допомогою мікрометричного гвинта поступово змінювати ширину щілини від 0,03 мм до 0,42 мм з кроком 0,03 мм. Для кожного значення виміряти ширину 2 D головного максимуму. УВАГА! Слід дуже обережно працювати при показах барабана поблизу нуля і ні в якому разі не зводити його до нуля - це веде до виходу з ладу щілини.
5. Обчислити вирази та для відповідних значень , , та .
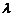6. Результати вимірювань та обчислень записати в таблицю 1.

Таблиця 1

№ п/п	L, м	λ, нм	, мм	2D, мм	D, мм	·10-9, м2	·10 -9 м2
		632,8
...

1. Побудувати графік залежності D= f( ).
2. Зменшити відстань L між щілиною та екраном наближено в два рази. Переконатися, що для нових значень D виконується співвідношення (3).
3. Проаналізувати отримані результати та зробити висновки.

Контрольні запитання

1. Як слід розуміти поняття корпускулярно-хвильовий дуалізм для мікрочастинок?
2. В чому полягає фізичний зміст співвідношення невизначеностей Гейзенберга?
3. Поясніть співвідношення невизначеностей Гейзенберга на прикладі руху фотонів крізь щілину.
4. Наведіть приклади фізичних явищ, які знаходять своє пояснення на основі співвідношення невизначеностей Гейзенберга.
5. Де використовуються хвильові властивості потоків мікрочастинок?
6. Чому для виконання даної роботи доцільно використати лазер?

Не нашли, что искали? Воспользуйтесь поиском: