Метод узловых и контурных уравнений

Метод узловых и контурных уравнений для расчета сложных электрических цепей подразумевает составление системы уравне­ний по законам Кирхгофа. При составлении системы уравнений должно учитываться следующее.

1. Число уравнений равно числу токов в цепи (число токов рав­но числу ветвей в рассчитываемой цепи). Направление токов в ветвях выбирается произвольно.

2. По первому закону Кирхгофа составляется (п - 1) уравнений, где п —число узловых точек в схеме.

3. Остальные уравнения составляются по второму закону Кирх­гофа.

В результате решения системы уравнений определяются иско­мые величины для сложной электрической цепи (например, все токи при заданных значениях ЭДС источников Е и сопротивле­ний резисторов). Если в результате расчета какие-либо токи полу­чаются отрицательными, это указывает на то, что их направление противоположно выбранному.

Пример 4.9

Составить необходимое и достаточное количество уравнений по законам Кирхгофа для определения всех токов в цепи (рис. 4.12) методом узловых и контурный уравнений.

Решение

В рассматриваемой сложной цепи имеется 5 ветвей, следовате­льно, 5 различных токов, поэтому для расчета необходимо соста­вить 5 уравнений, причем 2 уравнения - по первому закону Кирхгофа (в цепи п = 3 узловых точки А, В и C)и 3 уравнения - по второму закону Кирхгофа (внутренним сопротивлением ис­точников пренебрегаем, т.е. R₀ = 0).

Составляем уравнения:

1) (для точки А);

2) 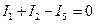(для точки В);

3) (для контура АаВ);

4) (для контура ABbC);

5) (для контура АСс).

Обход по часовой стрелке.

Пример 4.10

Определить токи в примере 4.7 методом узловых и контурных уравнений (схема рис. 4.10) при тех же заданных условиях.

Решение

При выбранном в схеме рис. 4.10 направлении токов составим необходимое и достаточное количество уравнений по законам Кирхгофа:

1) или ;

2) (обход по часовой стрелке);

3) (обход против часовой стрелки).

В уравнение (2) подставляются значения тока I₁ из уравнения (1) и числовые значения заданных величин. Тогда уравнения (2) и (3) будут выглядеть так:

2) ;

3) .

Для сокращения тока I₂ при суммировании уравнений (2) и (3) все числовые значения уравнения (3) умножаются на 2 (два).

2) ;

3) .

Результаты суммирования: .

Откуда A.

Из уравнения (3): А.

Рис. 4.12

И из уравнения (1): А. Очевидно, что полученный результат совпадает с результатом, полученным методом узлового напряжения.

Не нашли, что искали? Воспользуйтесь поиском: