Метод контурных токов.

Использует n = p – m уравнений по числу независимых контуров. Уравнения составляются только по 2-му закону Кирхгофа. 2-ой закон Кирхгофа устанавливает взаимосвязь напряжений в любом контуре цепи. Наличие в цепи идеальных источников тока (ИИТ) упрощает задачу анализа, так как сокращается число необходимых уравнений, поскольку ток ИИТ сразу определяет соответствующий контурный ток. ИИТ должен входить только в один из независимых контуров. При наличии в схеме реальных источников тока (РИТ) необходимо либо:

1. Заменить РИТàРИН ;

2. Рассматривать РИТ как отдельный контур с ИИТ, контурный ток которого определяется током источника.

Метод контурных токов использует следующие основные понятия:

Контурный ток - условный ток произвольного направления, протекающий в каждом независимом контуре ;

Собственное сопротивление контура - алгебраическая сумма сопротивлений всех элементов контура ;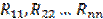

Взаимное сопротивление смежных контуров - сопротивление общего для двух контуров элемента 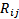, i,j - номера смежных контуров, причем R_ij = R_ji; берется со знаком «+», если направления контурных токов совпадают на общем элементе, и с «-«, если противоположны;

Контурная ЭДС - алгебраическая сумма всех ЭДС каждого независимого контура ; берется со знаком «+», если ее направление совпадает с направлением контурного тока.

Алгоритм метода контурных токов состоит из четырех основных этапов:

1. Выбор n- независимых контуров, произвольное обозначение направления контурных токов и токов ветвей; при этом ИИТ должны входить только в один какой-либо контур, поскольку они определяют величину контурного тока.

2. Запись системы стандартизованных линейных уравнений для всех независимых контуров, нахождение собственных и взаимных сопротивлений и контурных ЭДС для данной системы.

3. Решение системы в матричной форме или по методу Крамера относительно контурных токов.

4. Определение токов в ветвях по методу наложения полученных значений контурных токов.

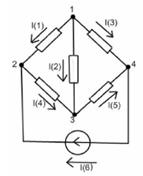
Рассмотрим этот алгоритм на примере данной схемы, произвольно выбирая направления контурных токов и токов в ветвях.

1. В схеме 4 независимых контура, причем I_k4 = I (или можно было заменить РИТ на РИН с E = IR₂). (E-ЭДС)

2. Для трех оставшихся независимых контуров получим следующую систему уравнений:

где R₁₁ = R₁+R₃+R₆; R₂₂ = R₂+R₃+R₄; R₃₃ = R₄+R₅+R₆;

R₁₂=R₂₁= - R₃; R₁₄=0; R₂₃=R₃₂= - R₄; R₂₄=R₂; R₁₃=R₃₁= - R₆; R₃₄=0.

3. Полученные значения сопротивлений и ЭДС необходимо подставить в исходную систему уравнений и решить ее матричными или другими известными способами. Для этого необходимо последнее слагаемое из левой части перенести в правую:

Тогда решение в матричной форме: ;

где ; i=1,…,n; ∆ - определитель матрицы [R]; ∆_I – определитель, в котором вместо i -го столбца стоит матрица-столбец [E].

4. Токи ветвей: i₁= I_k1; ; ; ; ; .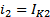

Таким образом, для внешних ветвей значения токов совпадают с контурными; для смежных – равны разности контурных токов соответствующих контуров.

6 Топологические методы формирования уравнений, описывающих электрическую цепь.

Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения, который называется топологией цепи. Основными понятиями, используемыми при рассмотрении топологии цепей, являются следующие:

1) Ветвь - участок цепи, обтекаемый одним и тем же током. Направления токовизначально выбираются произвольно.

2) Узел - место соединения трех и более ветвей.

количество узлов;
количество ветвей.

Поскольку топологические или геометрические свойства цепей не зависят от типа, параметров и количества элементов, в них входящих, то каждую ветвь цепи можно заменить отрезком линии, и такое условное изображение схемы называется графом электрической цепи.

Отрезок, соединяющий 2 узла и соответствующий ветви схемы, называются ветвью графа. При этом узлам схемы соответствуют узлы графа.

Граф, у которого все ветви ориентированы, называется ориентированным графом. Подграфом называется любая часть графа, т.е. это может быть одна ветвь или один изолированный узел, а также любое множество ветвей и узлов графа.

В теории цепей основными являются следующие подграфы:
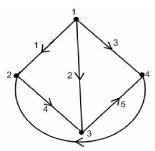
1. Путь - упорядоченная последовательность ветвей, в которой каждые две соседние имеют один общий узел, и при этом каждая ветвь и каждый узел встречаются на этом пути только один раз. Например: 1-4-5, 2-4-6, 3-5-4, 6-4-2, 2-4, 2-5-6, 2-5, 4-2-3. Таким образом, путь - это совокупность ветвей, проходимых непрерывно.

2. Контур - замкнутый путь, в котором один из узлов является начальным и конечным одновременно. Из рисунка 1 определим контуры: 1-4-5-3, 1-6-3, 4-5-6, 2-3-5. Если между любой парой узлов графа существует связь, то такой граф называется связным.

3. Дерево - связный подграф, содержащий все узлы, но ни одного контура.

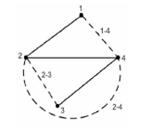
4. Ветви связи (дополнения дерева) - это ветви графа, дополняющие дерево до исходного графа.

(2-3, 1-4, 2-4).

5. Сечение - это множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых может быть отдельным узлом. Сечение можно изобразить в виде замкнутой поверхности, рассекающей соответствующие ветви.

Сечение Si отсекает 3,5,6 ветви; S2 отсекает 1,2,5,6 ветви.

Любой ориентированный граф формально может быть описан при помощи так называемой матрицы соединений, состоящей из q-строк (количество узлов) и р-столбцов (количество ветвей). При этом на пересечении i-ой строки (i= 1, q) и j-ro столбца (j=l, р) будут находиться:

1. +1 - если ток втекает в i-й узел по ветви].

2. -1 - если ток вытекает из i-oro узла по ветви].

3. О - когда к i-му узлу ветвь не подсоединена.

Такая матрица, состоящая из q-строк и р-столбцов, содержит линейно зависимые строки, т.е. сумма элементов любого столбца равна нулю. Это означает, что одна любая из строк является излишней, поскольку может быть получена путем линейной (любой) комбинации остальных. Следовательно, число независимых строк или узлов в любой схеме замещения: m = q - 1, поэтому для анализа графов используют редуцированные матрицы (М_р), полученные из исходной с помощью удаления любой строки.

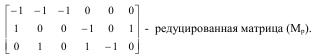
Не нашли, что искали? Воспользуйтесь поиском: