
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Требования к вычислительным алгоритмам (корректность, обусловленность и т.д.) и к их программным реализациям.
Вычислительный алгоритм – точное предписание действий над входными данными, задающие вычислительный процесс, направленный на преобразование входных данных в полностью определяемый этими данными результат.
Вычислительный алгоритм складывается из 2-х частей:
1. Абстрактный – записанный математическими знаками
2. Программный – программа, записанная на языке программирования
К вычислительным алгоритмам в целом предъявляются требования корректности и хорошей обусловленности.
Требования к абстрактным вычислительным алгоритмам:
1. Экономичность (число операций)
2. Точность (обеспечение приемлемой погрешности)
3. Экономия памяти (большие массивы данных)
4. Простота алгоритма
Требования к программным реализациям:
1. Надежность (отсутствие ошибок, получение нужного результата)
2. Работоспособность (способность программы выявлять недопустимые данные и обнаруживать критические для алгоритма ситуации)
àa
àb
if (b’ = 0)
c = a/b
else MessageBox show (“…”)
cà
3. Переходимость (возможность работы на различных платформах и операционных системах без изменений)
4. Поддерживаемость (легкость модификации программы)
5. Простота в использовании
Схема
1) Постановка задачи
1.1. Формулировка задачи, выбор параметров
1.2. Определение цели и критериев, качеств, описание задачи
2) Составление математического описания
2.1. Аналитические методы
2.2. Экспериментальные методы
2.3. Экспериментально-аналитические методы
3) Составление алгоритма и «написание» программы
3.1. Выбор численных методов
3.2. Составление алгоритма
3.3. Программирование
3.4. Отладка программы
4) Установление адекватности модели объекту
5) Использование модели
10) Решение нелинейных уравнений – общие вопросы (форма записи задачи, основные этапы решения нелинейных уравнений, методы решения нелинейных уравнений).
f(x,P1,P2,P3,Pn)=0
Решение нелинейных уравнений
1этап) Локализация отрезков: Определить интервал изменения функции на котором существует ровно один корень.
Локализация:
1теорема) Если значение функции на концах интервалов имеют разные знаки, то на нем будет как минимум 1 корень, f(a)*f(b)<0
2)теорема) Если производная функции на концах отрезка существует и сохраняет свой знак в пределах отрезка, то на нем будет ровно 1 корень
2этап) Поиск корня на заданном отрезке локализации с заданной точностью, которая определяется 3 способами:
1)по ширине интервала a,b: |b-a|<E
2)по абсолютной погрешности значения функции |f(x)|<E
3)относительная погрешность (в долях или процентах) |(f(x)-y)/y|<E
На 2 этапе используются конкретные методы решения нелинейных уравнений:
-бисекции(половинного деления,
-хорд
-касательных
-метод простых итераций
Метод бисекции
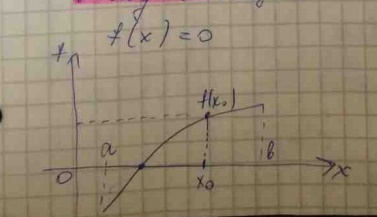
1. Разбиваем отрезок пополам:
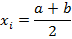
2. Вычисление погрешности δ.
3. Сравнение погрешности с допустимой ε = 0.5%
Если δ < ε -> вывод результата
Если δ > ε -> возвращение в начало
Достоинства метода: гарантированная сходимость и простота реализации.
Недостаток: низкая скорость сходимости.
Справедливы для возрастающей функции. В случае убывающей функции условие будет обратным:

Метод хорд
Предназначен для уточнения корня на интервале [а,b]. Очередное приближение согласно этому методу задается в точке x0, где пересекается прямая линя проведенная через точки f(a), f(b). Эта линия называется хордой. Соотношение, с помощью которого определяется значение последующего приближения можно вывести из обобщенного уравнения прямой линии, проходящей через 3 точки. 
После некоторых преобразований получаем 
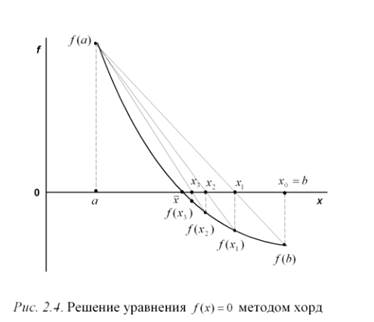
Затем по найденному значению xi определяют значение функции f(xi). Если  , то процесс решения и нахождения корня уравнения заканчивается, если же условие не выполняется, то производят сужение интервала поиска так, чтобы значения функции на концах отрезка имели разные знаки.
, то процесс решения и нахождения корня уравнения заканчивается, если же условие не выполняется, то производят сужение интервала поиска так, чтобы значения функции на концах отрезка имели разные знаки. 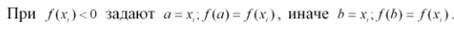
После чего вычисляют новое значение приближения и повторяют весь итерационный процесс. Метод быстрее метода бисекции
Метод касательных.
Метод основан на замене функции в точке начального приближения x0=a или x0=b касательной, пересечение которой с осью x дает последующее приближение xi
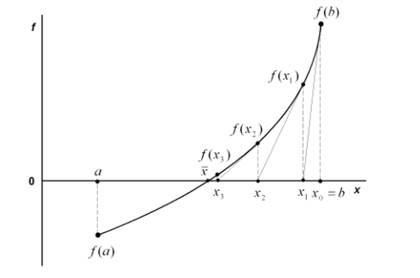
Уравнение касательной 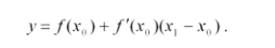
Из этого уравнения получаем точку пересечения 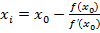
Достоинства: простота, логическая стройность, высокая скорость
Недостатки: необходимость вычисления производной, локальная сходимость
- Решение нелинейных уравнений – метод простых итераций.
 (3.1)
(3.1)
где  – заданная функция;
– заданная функция; 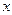 – неизвестная величина;
– неизвестная величина; 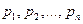 – параметры задачи.
– параметры задачи.
От исходного уравнения (3.1) выполняется переход к эквивалентному уравнению
 . (3.7)
. (3.7)
Выбирается каким-либо способом грубо начальное приближенное значение корня 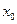 и подставляется в правую часть уравнения (3.7). Получается новое приближение
и подставляется в правую часть уравнения (3.7). Получается новое приближение
 .
.
Подставляя каждый раз новое значение корня в (3.7), получают последовательность значений
 . (3.8)
. (3.8)
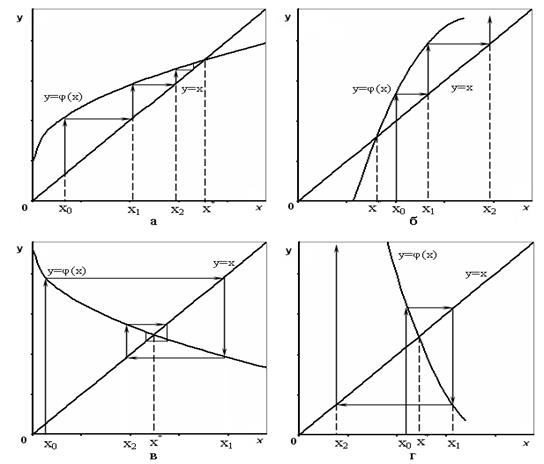
Рис. 3.7. Метод простых итераций
Из графиков (рис. 3.7) видно, что возможен как сходящийся, так и расходящийся итерационные процессы. Скорость сходимости зависит от абсолютной величины производной 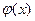 . Чем меньше
. Чем меньше  вблизи корня
вблизи корня 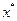 , тем быстрее сходится процесс.
, тем быстрее сходится процесс.
Установим критерий сходимости математически. Будем считать, что в итерационной формуле (3.8)
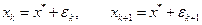 ,
,
где  и
и  – отклонения
– отклонения  и
и 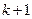 приближения от корня. Если процесс уточнения осуществляется вблизи корня
приближения от корня. Если процесс уточнения осуществляется вблизи корня 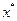 , то функцию
, то функцию 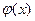 можно приближенно представить двумя членами ряда Тейлора. Тогда итерационная формула (3.8) примет вид
можно приближенно представить двумя членами ряда Тейлора. Тогда итерационная формула (3.8) примет вид
 ,
,
но так как 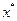 является корнем уравнения, то
является корнем уравнения, то 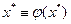 и, следовательно,
и, следовательно,
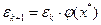 .
.
Для того чтобы итерационный процесс был сходящимся, необходимо выполнить условие
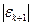 <
< 
или
 <
< 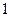 . (3.9)
. (3.9)
Переход от уравнения (3.1) к уравнению (3.7) можно осуществить различными способами в зависимости от вида функции 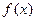 . При таком переходе необходимо построить функцию
. При таком переходе необходимо построить функцию 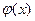 так, чтобы выполнялось условие сходимости (3.9).
так, чтобы выполнялось условие сходимости (3.9).
Рассмотрим один из общих алгоритмов перехода от уравнения (3.1) к уравнению (3.8). Умножим левую и правую части уравнения (3.1) на произвольную константу 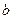 и добавим к обеим частям неизвестное
и добавим к обеим частям неизвестное 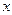 . При этом корни исходного уравнения не изменятся
. При этом корни исходного уравнения не изменятся
 . (3.10)
. (3.10)
Введем обозначение
 (3.11)
(3.11)
и перейдем от соотношения (3.10) к уравнению (3.7).
Произвольный выбор константы 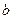 позволит обеспечить выполнение условия сходимости (3.9). Желательно выбрать величину
позволит обеспечить выполнение условия сходимости (3.9). Желательно выбрать величину 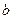 такой, чтобы
такой, чтобы 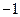 <
< 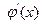 <
< 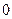 , тогда сходимость итерационного процесса будет двухсторонней (рис. 3.7, в). В этом случае в наиболее простом виде можно представить критерий окончания итерационного процесса
, тогда сходимость итерационного процесса будет двухсторонней (рис. 3.7, в). В этом случае в наиболее простом виде можно представить критерий окончания итерационного процесса
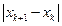 <
< 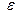 , (3.12)
, (3.12)
где 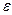 – заданная абсолютная погрешность вычисления корня.
– заданная абсолютная погрешность вычисления корня.
Если функция 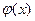 выбрана в виде (3.11), то производная по
выбрана в виде (3.11), то производная по 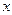 от этой функции будет
от этой функции будет
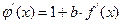 .
.
Наибольшую скорость сходимости получим при 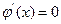 , тогда
, тогда
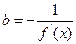
и итерационная формула (3.8) переходит в формулу Ньютона

Метод Ньютона имеет самую высокую скорость сходимости из всех итерационных процессов.
Метод Крамера

Метод Гаусса

18.Методы решения систем линейных алгебраических уравнений – итерационные методы (Якоби, Зейделя).
Якоби:
Задаемся начальными приближениями всех неизвестных
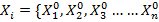 }
}
Подставляем эти значения в правую часть системы неизвестных на след. Итерацию.

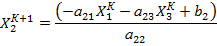
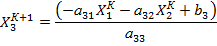
Проверяем погрешность

Зейделя
Отличается тем, что в правую часть подставляются Х уже найденные на текущей итерации.

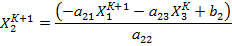
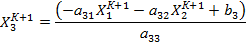
Не нашли, что искали? Воспользуйтесь поиском: