ДЕРЕВЬЯ. ОПРЕДЕЛЕНИЯ, КЛАССИФИКАЦИЯ, СПОСОБЫ ПРЕДСТАВЛЕНИЯ.

Дерево с базовым типом Т – это:

1) Либо пустое дерево

2) Либо вершина типа Т с конечным числом связанных с ней отдельных деревьев с базовым типом Т (поддеревья).

(Дерево, на которое ссылается какая-либо вершина – поддерево)

1

2

Глубина(высота) = 3

Вершина, на которую непосредственно ссылается другая вершина – ее потомок. Обратная вершина – предок.

Вершина, у которой нет потомков – лист дерева.

Если пронумеруем вершины так, чтобы каждый следующий потомок был на уровень выше, то вершина, находящаяся на 0 уровне – корень дерева.

Вершина, которая не является листом – внутренняя вершина.

Уровень какой-либо вершины – глубина (высота), а глубина самого дерева - максимальная глубина из всех ее вершин.

Количество непосредственных потомков вершины называется степенью данной вершины, степень дерева – максимальная из всех возможных степеней.

Число ветвей (ребер), которые необходимо пройти от корня к вершине х, называется длиной пути к х (корень имеет путь 0).

Длина пути всего дерева (длина внутреннего пути) – сумма длин путей до всех его вершин.

Средняя длина пути определяется по формуле: .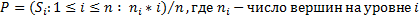

Дерево называется упорядоченным, если все ветви, исходящие из любой вершины, также являются упорядоченными.

И - разные!

Упорядоченные деревья второй степени называются двоичными деревьями.

Деревья n-ной (большей 2) степени называются сильно ветвящимися.

Деревья, имеющие минимальную высоту, называются идеально сбалансированными (количество вершин в левом и правом поддереве отличаются не больше чем на 1 – условие для всех вершин).

Выражение таких рекурсивных структур требует использования ссылок.

Существует множество различных способов представления деревьев (на примере бинарного дерева):

1) Списочное представление бинарных деревьев основано на элементах, соответствующих узлам дерева. Каждый элемент имеет поле данных и два поля указателей. Один указатель используется для связывания элемента с правым потомком, а другой – с левым. Листья имеют пустые указатели потомков. При таком способе представления дерева обязательно следует сохранять указатель на узел, являющийся корнем дерева.

Можно заметить, что такой способ представления имеет сходство с простыми линейными списками. И это сходство не случайно. На самом деле рассмотренный способ представления бинарного дерева является разновидностью мультисписка, образованного комбинацией множества линейных списков. Каждый линейный список объединяет узлы, входящие в путь от корня дерева к одному из листьев.

struct bynary_tree{

Tdata data;

struct binary_tree *left;

struct binary_tree *right;

}

или

struct TREE

{
int Info;
TREE *Right;
TREE *Left;
};

Для обработки дерева достаточно знать адрес корневой вершины. Для хранения этого адреса надо ввести ссылочную переменную:
TREE *Root;

Тогда пустое дерево просто определяется установкой переменной Root в нулевое значение:
Root = NULL;

2) В виде массива проще всего представляется полное бинарное дерево, так как оно всегда имеет строго определенное число вершин на каждом уровне. Вершины можно пронумеровать слева направо последовательно по уровням и использовать эти номера в качестве индексов в одномерном массиве.

Если число уровней дерева в процессе обработки не будет существенно изменяться, то такой способ представления полного бинарного дерева будет значительно более экономичным, чем любая списковая структура.

Однако далеко не все бинарные деревья являются полными. Для неполных бинарных деревьев применяют следующий способ представления. Бинарное дерево дополняется до полного дерева, вершины последовательно нумеруются. В массив заносятся только те вершины, которые были в исходном неполном дереве. При таком представлении элемент массива выделяется независимо от того, будет ли он содержать узел исходного дерева. Следовательно, необходимо отметить неиспользуемые элементы массива. Это можно сделать занесением специального значения в соответствующие элементы массива. В результате структура дерева переносится в одномерный массив. Адрес любой вершины в массиве вычисляется как: адрес , где k-номер уровня вершины, i- номер на уровне k в полном бинарном дереве. Адрес корня будет равен единице. Для любой вершины можно вычислить адреса левого и правого потомков: адрес_L и адрес_R

Главным недостатком рассмотренного способа представления бинарного дерева является то, что структура данных является статической. Размер массива выбирается исходя из максимально возможного количества уровней бинарного дерева. Причем чем менее полным является дерево, тем менее рационально используется память.

Не нашли, что искали? Воспользуйтесь поиском: