
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
АВЛ-СБАЛАНСИРОВАННЫЕ ДЕРЕВЬЯ. ОПЕРАЦИИ, СЛОЖНОСТЬ.
АВЛ-сбалансированное дерево – двоичное дерево, сбалансированное по высоте, в котором высоты поддеревьев каждой из вершин отличаются не больше, чем на 1.
Пример АВЛ – деревья Фибоначчи, где каждое следующее строится на основе двух предыдущих.
Формула, определяющая количество вершин для дерева Ф. n-ого порядка – рекурсивная:
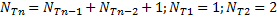 .
.
За время О(log n) можно сделать операции включения вершины с данным ключом, исключения, найти вершину с данным ключом.
АВЛ никогда не будет выше ИДБ чем на 45%:
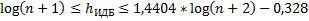
Операция вставки:
Проход по пути поиска, включение и проверка на нарушение баланса, балансировка.
Пусть новый узел вставляется в L, увеличивая его высоту на 1, тогда имеют место 3 случая:
1) hl=hr: после вставки высота становится неравной, но критерий балансировки не нарушается
2) hl<hr: высоты становятся равными, баланс только улучшается
3) hl>hr: критерий балансировки нарушается, и дерево требуется перестроить
Рассматриваем 4 случая (случай 3 и 4 – зеркальные отображения случаев 1 и 2 соответственно):
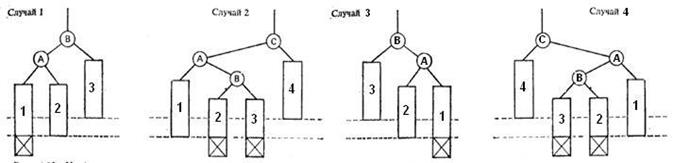
Одигарный поворот(LL) Двойной поворот(LR) (RR) (RL)

Алгоритм определения типа поворота (при добавлении в левое поддерево, с правым наоборот):
1) Находим ближайшую к низу вершину, которая является разбалансированной.
2) Рассмотрим ее левое поддерево. Если левое поддерево этого поддерева выше правого, то случай 1, иначе – случай 2.
3) Расставляем буквы и цифры, осуществляем поворот согласно схемам.
Сложность операции балансировки предполагает, что АВЛ используют, когда поиск проиcходит чаще, чем включение, иначе следует брать СДБ.
Операция изменения ссылок не зависит от размера дерева и составляет O(1), операция просмотра сверху вниз O(log n)итого – O(1)+2 O(log n).
Пример:

Операция удаления – как в дереве поиска + балансировка

Операции вставки и удаления – происходят как в дереве поиска, при этом после каждого действия требуется проверка на нарушение баланса и, при необходимости, выполнение балансировки по указанной схеме.
В среднем случае: на 2 включения 1 балансировка. А при удалении поворот в 1 случае из 5.
Процедура удаления из сбалансированного дерева строится на основе алгоритма удаления из обычного дерева. Простые случаи – концевые узлы и узлы с единственным потомком.
В худшем случае удаление проводится за O(logn).
Не нашли, что искали? Воспользуйтесь поиском: