Однорозрядні суматори

Логічна схема, яка виконує додавання значень i-х розрядів Х_i і Y_i двійкових чисел з урахуванням перенесення Z_i з молодшого сусіднього розряду і виробляє на виходах функції результат S_i і перенесення P_i в старший сусідній розряд називається однорозрядним суматором. На основі однорозрядних схем додавання на три входи і два виходи будуються багаторозрядні суматори будь-якого типу. Алгоритм роботи однорозрядного суматора відображається таблицею істинності (табл. 3.20).

Таблиця 3.20. Алгоритм роботи однорозрядного суматора.

На основі таблиці 3.20 записується система логічних функцій для результату S_i і перенесення Р_i:

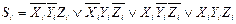(3.31)

(3.32)

Мінімізацію функцій (3.31) і (3.32) за допомогою карт Карно показано на рис. 3.30.

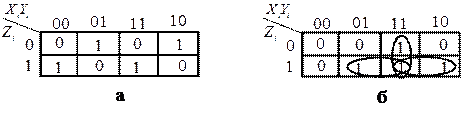
Рис. 3.30. Карти Карно для мінімізації функцій: а – S_i; б – P_i

Як видно з карт Карно, функція результату S_i не мінімізується, а функція Р_i мінімізується з пониженням рангу кон'юнкції і використовує тільки прямі значення змінних:

(3.33)

При проектуванні комбінаційних однорозрядних суматорів враховують наступні чинники:

· схема повинна характеризуватися регулярністю (подібністю) структури і мінімальною вартістю;

· з метою підвищення швидкодії багаторозрядного суматора потрібний мінімальний час отримання функції перенесення;

· t _П = кt _Р, де к – число послідовно включених елементів від входів до виходів P_i або ; t_Р – середня затримка розповсюдження сигналу одним логічним елементом у вибраній серії інтегральних мікросхем; параметр часто називають каскадністю (поверховістю) схем, таким чином, для мінімізації часу отримання перенесення необхідно зменшити каскадність схеми і використовувати інтегральні мікросхеми з малим часом затримки розповсюдження сигналу;

· для схем однорозрядних суматорів на основі рівнянь (3.31) і (3.32) необхідно виробляти як прямі P_i, так і інверсні значення функції перенесення, яку називають парафазною.

Рівняння (3.31) і (3.32) можуть бути виражені через функцію "Виключальне АБО ":

(3.34)

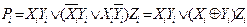(3.35)

Схему однорозрядного суматора на елементах "Виключальне АБО" згідно рівнянням (3.34) і (3.35) показано на малюнку 3.23б. Її вартість складає вісім входів, каскадність к дорівнює 2.

Логічна схема, яка виконує додавання значень i -хрозрядів Х_i і Y_i двійкових чисел Х і Y і реалізує на виході значення результату М_i і перенесення в старший сусідній розряд R_i називається напівсуматором:

(3.36)

а б

Рис. 3.31. Однорозрядний суматор з використанням власного перенесення: а – схема, б – часова діаграма роботи

Таким чином, напівсуматор виконує лише частину завдання підсумовування в i -мрозряді, оскільки не враховує перенесення з сусіднього молодшого розряду. Схему напівсуматора, побудовану на основі рівнянь (3.36), показано на рис. 3.31. З рівнянь (3.34) і (3.35) виходить, що схема однорозрядного суматора може бути побудована на основі двох напівсуматорів і додаткового логічного елементу АБО, як показано на рис. 3.31.

Не нашли, что искали? Воспользуйтесь поиском: