
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определение численности выборки
Разрабатывая программу выборочного наблюдения, задают величину допустимой ошибки D и доверительную вероятность Р. Неизвестным является тот минимальный объем выборки n, который должен обеспечить заданную точность.
Формулы для определения численности выборки приведены в таблице
| Метод отбора | Для оценки средней | Для оценки доли |
| Повторный | 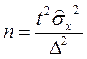
| 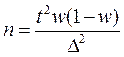
|
| Бесповторный | 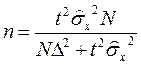
| 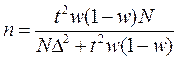
|
Величины  , w оцениваются по выборке меньшего размера. Часто в качестве w выбирается 0,5 (по наихудшему случаю).
, w оцениваются по выборке меньшего размера. Часто в качестве w выбирается 0,5 (по наихудшему случаю).
Пример.
Рассмотрим пример оценки доли полезного использования рабочего времени на предприятии (генеральной совокупности). Допустим, что предварительных данных об использовании рабочего времени нет. Допустимую ошибку установим в размере 0,05, а уровень значимости 0,05 (доверительная вероятность равна 0,95). Тогда необходимое число наблюдений составит
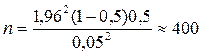 наблюдений.
наблюдений.
Допустим, что по данным 1000 наблюдений получено, что время полезной работы наблюдается в 90 % наблюдений. Используя приведенную выше формулу, можно определить среднеквадратичную ошибку оценки доли полезного времени
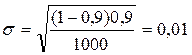 .
.
Предельная ошибка выборочной доли составляет 0,02. Поэтому с вероятностью 0,95 можно утверждать, что истинное значение доли полезно используемого рабочего времени находится в диапазоне (0,88 – 0,92), т. е. составляет от 88 до 92 %.
Задание 4.
Результаты моментного наблюдения за поведением покупателей в магазине самообслуживания приведены в таблице.
| Код действия покупателя | |||||||
| Количество покупателей |
1 − ищут нужный отдел;
2 − подходят к прилавку;
3 − изучают ассортимент товаров и их цены;
4 − выбирают необходимый товар;
5 − переносят товар к кассе;
6 − оплачивают товар;
7 − выходят из магазина.
Найти выборочную долю покупателей, которые в момент обследования совершают действие, которое указано в таблице в соответствии с номером варианта задания.
| Вариант | Код действия | Вариант | Код действия |
| 3 или 4 | |||
| 5 или 6 | |||
| 1 или 2 |
и предельную ошибку для оценки доли в генеральной совокупности с доверительной вероятностью Р = 0,95.
9. КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ 
Во многих науках (физика, экономика и т. д.) используются модели, в которых некоторые переменные (не случайные) связаны функциональной зависимостью. Примером таких зависимостей является закон Бойля-Мариотта или формула Ф. Котлера.
При статистической зависимости переменные (случайные величины) не связаны функционально. Однако закон распределения одной из них зависит от того, какое значение приняла другая случайная величина. Поэтому речь идет об условном распределении Y при заданном х.
В частности, можно рассматривать M(Y/x) как некоторую функцию х (регрессия).
При исследовании статистической зависимости между признаками пытаются ответить на следующие вопросы:
- существует ли статистическая связь между признаками;
- какова степень этой связи;
- какова форма связи.
Первые два вопроса решаются на основании корреляционного анализа. В качестве меры тесноты связи обычно используется коэффициент корреляции - 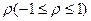 . При
. При  связь становится функциональной.
связь становится функциональной.
Выборочный коэффициент корреляции r рассчитывается по формуле
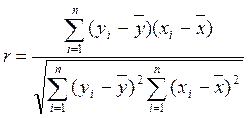 .
.
где 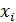 - значение случайной величины X для i -го наблюдения (объекта);
- значение случайной величины X для i -го наблюдения (объекта);
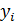 - значение случайной величины Y для i -го наблюдения (объекта);
- значение случайной величины Y для i -го наблюдения (объекта);
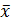 ,
, 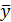 - выборочные средние значения случайных величин X и Y;
- выборочные средние значения случайных величин X и Y;
n – число наблюдений (объем выборки).
На практике используются следующие формулы для «ручных» вычислений
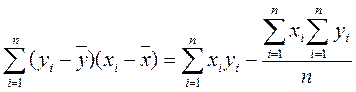 ;
;
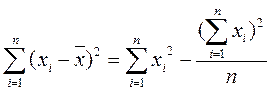 ;
;
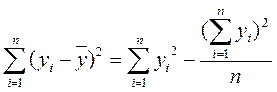 .
.
После того, как вычислен выборочный коэффициент корреляции r следует проверить гипотезу об отсутствии корреляционной связи для генеральной совокупности Н0: 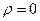 .
.
Для этого вычисляется критерий

и сравнивается с табличным значением 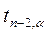 критерия Стьюдента с
критерия Стьюдента с  степенями свободы уровня значимости
степенями свободы уровня значимости 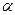 .
.
Если 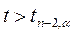 , то с надежностью
, то с надежностью 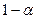 можно отвергнуть гипотезу Н0 и считать, что корреляция имеется.
можно отвергнуть гипотезу Н0 и считать, что корреляция имеется.
Для измерения тесноты связи используется не только коэффициент корреляции, но и корреляционное отношение.
Рассмотрим аналитическую группировку. Имеет место следующее соотношение
 ,
,
где 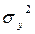 − полная дисперсия признака-результата;
− полная дисперсия признака-результата;
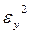 − внутригрупповая дисперсия;
− внутригрупповая дисперсия;
 − межгрупповая дисперсия.
− межгрупповая дисперсия.
Внутригрупповая дисперсия характеризует ту часть дисперсии признака-результата, которая не зависит от признака-фактора. Ее оценка определяется по формуле
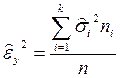 ,
,
где 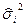 - оценка дисперсии признака – результата в пределах отдельной
- оценка дисперсии признака – результата в пределах отдельной
группы по признаку-фактору;
ni – численность i-й группы.
Межгрупповая дисперсия отражает ту часть общей дисперсии признака-результата, которая объясняется влиянием признака-фактора. Ее оценка определяется по формуле
 ,
,
где 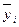 − групповое среднее i-й группы.
− групповое среднее i-й группы.
Коэффициент детерминации определяет долю объясненной дисперсии в общей дисперсии признака-результата
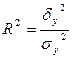 .
.
Корреляционное отношение определяется как
 .
.
Оно является мерой тесноты связи при любой форме зависимости, а не только линейной, как коэффициент корреляции.
Не нашли, что искали? Воспользуйтесь поиском: