
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Векторные диаграммы являются совокупностью векторов, изображающих действующие синусоидальные ЭДС и токи или их амплитудные значения.
Гармонически изменяющееся напряжение определяется выражением u = Um sin (ωt + ψи).
Расположим под углом ψи относительно положительной оси абсцисс х вектор Um, длина которого в произвольно выбранном масштабе равна амплитуде изображаемой гармонической величины (рис. 1). Положительные углы будем откладывать в направлении против вращения часовой стрелки, а отрицательные — по часовой стрелке. Предположим, что вектор Um, начиная с момента времени t = 0, вращается вокруг начала координат против часовой стрелки с постоянной частотой вращения ω, равной угловой частоте изображаемого напряжения. В момент времени t вектор Um повернется на угол ωt и будет расположен под углом ωt + ψи по отношению к оси абсцисс. Проекция этого вектора на ось ординат в выбранном масштабе равна мгновенному значению изображаемого напряжения: u = Um sin (ωt + ψи).
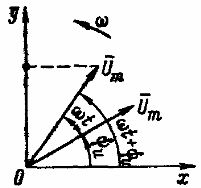
Рис. 1. Изображение синусоидального напряжения вращающегося вектора
Следовательно, величину, изменяющуюся гармонически во времени, можно изображать вращающимся вектором. При начальной фазе, равной нулю, когда u= 0, вектор Um для t = 0 должен быть расположен на оси абсцисс.
График зависимости любой переменной (в том числе и гармонической) величины от времени называется временной диаграммой. Для гармонических величин по оси абсцисс удобнее откладывать не само время t, а пропорциональную ему величину ωt. Временные диаграммы полностью определяют гармоническую функцию, так как дают представление о начальной фазе, амплитуде и о периоде.
Обычно при расчете цепи нас интересуют только действующие ЭДС, напряжения и токи или амплитуды этих величин, а также их сдвиг по фазе относительно друг друга. Поэтому обычно рассматриваются неподвижные векторы для некоторого момента времени, который выбирается так, чтобы диаграмма была наглядной. Такая диаграмма называется векторной диаграммой. При этомуглы сдвига по фазе откладываются в направлении вращения векторов (против часовой стрелки), если они положительные, и в обратном направлении, если они отрицательные.
Если, например, начальный фазовый угол напряжения ψи больше начального фазового угла ψi то сдвиг по фазе φ = ψи - ψi и этот угол откладывается в положительном направлении от вектора тока.
При расчете цепи переменного тока часто приходится складывать ЭДС, токи или напряжения одной и той же частоты.
Предположим, что требуется сложить две ЭДС: e1 = E1m sin (ωt + ψ1e)и e2 = E2m sin (ωt + ψ2e).
Такое сложение можно осуществить аналитически и графически. Последний способ более нагляден и прост. Две складываемые ЭДС е1 и е2 в определенном масштабе представлены векторами E1mE2m (рис. 2). При вращении этих векторов с одной и той же частотой вращения, равной угловой частоте, взаимное расположение вращающихся векторов остается неизменным.
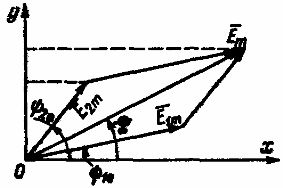
Рис. 2. Графическое сложение двух синусоидальных ЭДС одинаковой частоты
Сумма проекций вращающихся векторов E1m и E2m на ось ординат равна проекции на ту же ось вектора Em, являющегося их геометрической суммой. Следовательно, при сложения двух синусоидальных ЭДС одной и той же частоты получается синусоидальная ЭДС той же частоты, амплитуда которой изображается вектором Em, равным геометрической сумме векторов E1m и E2m: Em = E1m + E2m.
Векторы переменных ЭДС и токов являются графическими изображениями ЭДС и токов в отличие от векторов физических величин, имеющих определенное физическое значение: вектора силы, напряженности поля и других.
Указанный способ можно применить для сложения и вычитания любого числа ЭДС и токов одной частоты. Вычитание двух синусоидальных величин можно представить в виде сложения: e1- e2 = e1+ (- e2), т. е. уменьшаемая величина складывается с вычитаемой, взятой с обратным знаком. Обычно векторные диаграммы строятся не для амплитудных значений переменных ЭДС и токов, а для действующих величин, пропорциональных амплитудным значениям, так как все расчеты цепей обычно выполняются для действующих ЭДС и токов.
31. 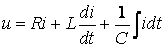 .
.
Найдем решение этого уравнения при условии, что
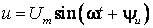 .
.
Будем рассматривать только частное решение уравнения с правой частью, т.к. общее решение с течением времени затухает и будет рассмотрено в разделе "Переходные процессы".
Поскольку цепь линейная, то при синусоидальном напряжении в установившемся режиме ток также будет синусоидален:
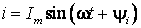 .
.
Найдём напряжение на участках цепи.
 . (2.18)
. (2.18)
Напряжение на резисторе по фазе совпадает с током.
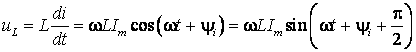 . (2.19)
. (2.19)
Напряжение на индуктивности по фазе опережает ток на угол 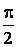 .
.
 . (2.20)
. (2.20)
Напряжение на конденсаторе отстаёт от тока по фазе на угол 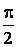 .
.
Сложим напряжения с помощью векторной диаграммы (рис. 2.8) в соответствии с уравнением
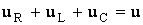 .
.
Угол  откладываем от тока против часовой стрелки, а
откладываем от тока против часовой стрелки, а  – от тока по часовой стрелке.
– от тока по часовой стрелке. 

Рисунок 2.8
Из прямоугольного треугольника:  .
.
 – закон Ома для амплитуд. (2.21)
– закон Ома для амплитуд. (2.21)
Введем обозначения:
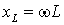 – индуктивное сопротивление;
– индуктивное сопротивление;
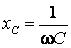 – ёмкостное сопротивление;
– ёмкостное сопротивление;
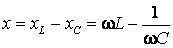 – реактивное сопротивление; (2.22)
– реактивное сопротивление; (2.22)
R – активное сопротивление;
 – полное сопротивление цепи переменного тока. (2.23)
– полное сопротивление цепи переменного тока. (2.23)
Тогда закон Ома для амплитудных значений запишется следующим образом:
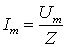 . (2.21а)
. (2.21а)
После деления обеих частей на  перейдем к действующим значениям:
перейдем к действующим значениям:
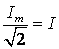 ;
; 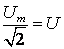 ;
;  . (2.24)
. (2.24)
Это закон Ома для действующих значений.
Из того же прямоугольного треугольника найдём угол сдвига фаз между током и напряжением:
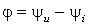 ;
; 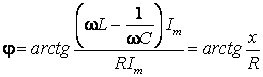 ;
;  . (2.25)
. (2.25)
Если 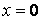 , то j = 0 – ток совпадает по фазе с напряжением; цепь имеет активный характер.
, то j = 0 – ток совпадает по фазе с напряжением; цепь имеет активный характер.
Если x > 0, то j > 0 – напряжение опережает ток, или ток отстаёт от напряжения по фазе; цепь носит индуктивный характер.
Если x < 0, то j < 0 – напряжение отстаёт от тока, или ток опережает напряжение по фазе; цепь носит ёмкостный характер.
Угол сдвига фаз j в простой цепи находится в следующих пределах: 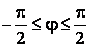 .
.
В цепи переменного тока кроме резисторов могут использоваться катушки индуктивности и конденсаторы. Для постоянного тока катушка индуктивности имеет только активное сопротивление, которое обычно невелико (если катушка не содержит большое количество витков). Конденсатор же в цепи постоянного тока представляет "разрыв" (очень большое активное сопротивление). Для переменного тока эти элементы обладают специфическим реактивным сопротивлением, которое зависит как от номиналов деталей, так и от частоты переменного тока, протекающего через катушку и конденсатор.
1.1. Катушка в цепи переменного тока. емкостные электронные датчики уровня надежены из-за отсутствия механических контактов
Рассмотрим, что происходит в цепи, содержащей резистор и катушку индуктивности. Колебания силы тока, протекающего через катушку:
 Основы электротехники выполнение курсовой работы Преобразовать соединение звездой сопротивлений в эквивалентное соединение треугольником сопротивлений
Основы электротехники выполнение курсовой работы Преобразовать соединение звездой сопротивлений в эквивалентное соединение треугольником сопротивлений
вызывают падение напряжения на концах катушки в соответствии с законом самоиндукции и правилом Ленца:

т.е. колебания напряжения опережают по фазе колебания силы тока на /2. Произведение LIm является амплитудой колебания напряжения:
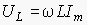
Произведение циклической частоты на индуктивность называют индуктивным сопротивлением катушки:
 (1)
(1)
поэтому связь между амплитудами напряжения и тока на катушке совпадает по форме с законом Ома для участка цепи постоянного тока:
 (2)
(2)
Как видно из выражения (1), индуктивное сопротивление не является постоянной величиной для данной катушки, а пропорционально частоте переменного тока через катушку. Поэтому амплитуда колебаний силы тока Im в проводнике с индуктивностью L при постоянной амплитуде UL напряжения убывает обратно пропорционально частоте переменного тока:
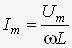 .
.
1.2. Конденсатор в цепи переменного тока.
При изменении напряжения на обкладках конденсатора по гармоническому закону: 
заряд q на его обкладках изменяется также по гармоническому закону:
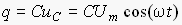 .
.
Электрический ток в цепи возникает в результате изменения заряда конденсатора, поэтому колебания силы тока в цепи будут происходить по закону:

Видно, что колебания напряжения на конденсаторе отстают по фазе от колебаний силы тока на /2. Произведение CUm является амплитудой колебаний силы тока:
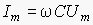
Аналогично тому, как было сделано с индуктивностью, введем понятие емкостного сопротивления конденсатора:
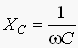 (3)
(3)
Для конденсатора получаем соотношение, аналогичное закону Ома:
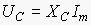 (4)
(4)
Формулы (2) и (4) справедливы и для эффективных значений тока и напряжения.
- Энергетический процесс- ДОДЕЛАТЬ111
В классической электротехнике достаточно полно определены и используются понятия активной P, реактивной Q, и полной мощности S линейной однофазной цепи. Эти мощности вычисляются один раз за интервал времени, равный периоду питающего напряжения. Такой же подход применяются и в трехфазных цепях без искажений кривой напряжения.
Особенностью трехфазных цепей, в данном случае, является то обстоятельство, что процесс энергопотребления можно и нужно рассматривать в каждый момент времени, даже на интервале периода питающего напряжения. Основной характеристикой процесса энергопотребления является скорость передачи или скорость необратимого преобразования электромагнитной энергии, или мгновенная мощность трехфазной цепи p(t), действующее значение которой и определяет уже известную активную мощность P, чей физический смысл заключается в средней за период скорости преобразования электромагнитной энергии, потребителем.
Другой особенностью трехфазных цепей [Бондаренко А.Е] является возможность использовать понятия мгновенной активной p(t), мгновенной реактивной q(t), мгновенной полной мощности s(t) и их физические датчикидля целей контроля и защиты параметров электроэнергетической системы, и расчетов.
Для объяснения предложенных здесь понятий, рассмотрим, для примера симметричную, активно – индуктивную трехфазную цепь, описываемую системой уравнений:
ua = L i1a + ia R;
ub = L i1b + ib R; uc = L i1c + ic R,
где:
ua,b,c – мгновенные фазные напряжения нагрузки,
ia,b,c – мгновенные фазные токи нагрузки,
i1a,b,c – производные мгновенных фазных токов,
L, R – индуктивность и активное сопротивление в фазе нагрузки.
Преобразуем вышеприведенные уравнения в одно, для чего умножим первое уравнениена “1”, второе на “exp(j120)”, третье на “exp(j240)”, а затем полученные уравнения сложим, в результате этого получим следующее комплексно - векторное выражение для активно – индуктивной нагрузки:
Uexp[j(γ+β+φ)] = Iexp[j(γ+β)] R+L(I1exp[j(γ+β)]+(γ 1+β 1)LI exp[j(γ+β+90)]) (1)
где:
I -модульизображающего вектора тока трехфазнойнагрузки,
I1 -производнаямодуляизображающего вектора тока,
U -модульизображающего вектора напряжения трехфазнойнагрузки,
R -активное сопротивление нагрузки,
L -индуктивность нагрузки,
γ = ωt -угол между вращающейся осью d (система координат d-q)и неподвижной фазной осью А (неподвижная трехфазная система координат),
β – уголмеждуосью d и изображающим вектором тока I,
φ – угол междуизображающим вектором тока и напряжением,
j – мнимая единица,
exp() – экспотенциальная функция.
33. В общем случае в цепях переменного тока обычно имеются все виды сопротивлений: активное, индуктивное и емкостное. Например, электрические двигатели переменного тока могут быть представлены эквивалентной схемой, состоящей из индуктивного сопротивления имеющихся в нем катушек и активного сопротивления образующих эти катушки проводов. Воздушные линии элек-
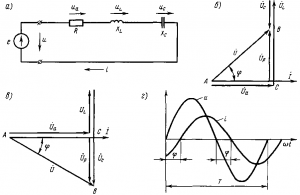 Рис. 192. Схема цепи переменного тока, содержащей последовательно включенные активное, индуктивное и емкостное сопротивления (а), векторные диаграммы (б и а), кривые тока и напряжения и (г)
Рис. 192. Схема цепи переменного тока, содержащей последовательно включенные активное, индуктивное и емкостное сопротивления (а), векторные диаграммы (б и а), кривые тока и напряжения и (г)
тропередачи или кабельные линии обычно представляют в виде совокупности активного, индуктивного и емкостного сопротивлений. Активное сопротивление обусловлено сопротивлением электрических проводов, индуктивное — индуктивностью линии, а емкостное — емкостью, возникающей между отдельными проводами, между проводами и землей или же между отдельными жилами кабеля и между жилами кабеля и его оболочкой.
Расчет электрических цепей переменного тока существенно отличается от расчета цепей постоянного тока, так как при переменном токе в активном, индуктивном и емкостном сопротивлениях имеют место различные сдвиги фаз между токами и напряжениями.
Ток, напряжение и полное сопротивление. При последовательном включении в цепь переменного тока активного R, индуктивного XL и емкостного Хс сопротивлений (рис. 192, а) к ним приложены напряжения: активное ua=iR, индуктивное uL = iXL и емкостное uc=iXc. Мгновенное значение напряжения и, приложенного к данной цепи, согласно второму закону Кирхгофа равно алгебраической сумме напряжений:
u = ua + uL + uc
Но для действующих значений эта формула неприменима, так как между всеми указанными напряжениями имеется сдвиг по фазе (амплитудные значения этих напряжений не совпадают по
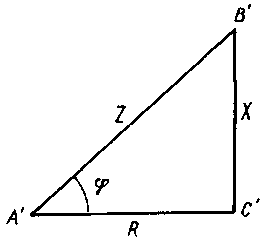 Рис. 193. Треугольник со противлении
Рис. 193. Треугольник со противлении
времени). Чтобы учесть сдвиг по фазе между напряжениями uа, uL и uc. осуществляют сложение их векторов:
? =?a +?L +?C
Для этого строят векторную диаграмму, на которой откладывают в определенном масштабе векторы тока? и напряжений?a,?L,?C. Из этих напряжений первое совпадает по фазе с током, второе опережает его на 90°. Векторная диаграмма (рис. 192,б) построена для цепи, в которой индуктивное сопротивление XL больше емкостного Xc (вектор?L, больше вектора?C.), а рис. 192, в — для цепи, в которой XL меньше Хс (вектор?L, меньше вектора?C). Вектор напряжения U является замыкающим — он сдвинут по фазе относительно вектора тока? на некоторый угол?. Напряжение U (действующее значение) может быть определено из треугольника ЛВС по теореме Пифагора:
U =?(U2a + (UL – Uc)2)
Таким образом, из-за наличия угла сдвига фаз? напряжение U всегда меньше алгебраической суммы Ua + UL + UC. Разность UL – UC = Up называется реактивной составляющей напряжения.
Рассмотрим, как изменяются ток и напряжение в последовательной цепи переменного тока.
В цепи, содержащей все три вида сопротивления, ток i и напряжение и оказываются сдвинутыми по фазе на некоторый угол ср (рис. 192, г), при этом 0<?<90°.
Полное сопротивление и угол сдвига фаз. Если подставить в формулу (71) значения Ua = IR; UL = l?L и UC=I/(?C), то будем иметь: U =?((IR)2+ [I?L-I/ (?С) ]2), откуда получаем формулу закона Ома для последовательной цепи переменного тока:
I = U / (? (R2+ [?L-1 / (?С) ]2)) = U / Z (72)
где Z =? (R2+ [?L-1 / (?С) ]2) =? (R2+ (XL– Xc)2)
Величину Z называют полным сопротивлением цепи, оно измеряется в омах. Разность?L — l/(?C) называют реактивным сопротивлением цепи и обозначают буквой X. Следовательно, полное сопротивление цепи
Z =? (R2+ X2)
Соотношение между активным, реактивным и полным сопротивлениями цепи переменного тока можно также получить по теореме Пифагора из треугольника сопротивлений (рис. 193). Треугольник сопротивлений А’В’С’ можно получить из треугольника напряжений ABC (см. рис. 192,б), если разделить все его стороны на ток I.
Угол сдвига фаз? определяется соотношением между отдельными сопротивлениями, включенными в данную цепь. Из треугольника А’В’С (см. рис. 193) имеем:
sin? = X / Z; cos? = R / Z; tg? = X / R
Например, если активное сопротивление R значительно больше реактивного сопротивления X, угол? сравнительно небольшой. Если в цепи имеется большое индуктивное или большое емкостное сопротивление, то угол сдвига фаз? возрастает и приближается к 90°. При этом, если индуктивное сопротивление больше емкостного, напряжение и опережает ток i на угол?; если же емкостное сопротивление больше индуктивного, то напряжение и отстает от тока i на угол?.
Временная и векторная диаграммы – Вопрос №30
Закон Ома для действующих и амплитудных значений тока и напряжения – Вопрос №31
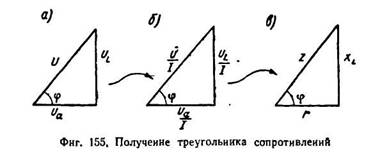
34. Если стороны треугольника напряжений (фиг. 155, а) разделить на ток I (фиг. 155, б), то углы треугольника от этого не из менятся, и мы получим новый треугольник, подобный первому — треугольник сопротивлений (фиг. 155, в).
|
В треугольнике сопротивления, показанном отдельно на фиг. 156, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.
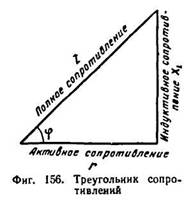
|
Из треугольника сопротивлений видно, что полное или кажущееся сопротивление z равно геометрической сумме активного r и индуктивного xL сопротивлений.
Применяя теорему Пифагора к треугольнику сопротивлений, получаем:
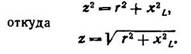
|
Если одно из сопротивлений цепи - (активное или реактивное), например, в 10 и более раз меньше другого, то меньшим можно пренебречь, в чем легко убедиться непосредственным расчетом.
ТРЕУГОЛЬНИК НАПРЯЖЕНИЙ - графическое изображение активного Ua, реактивного Ul и входного Uвх напряжений в цепи переменного тока с активным сопротивлением и индуктивностью.

Угол сдвига фаз между напряжением и током определяется из треугольника через
cos ф = Ua/U или tg ф = Ul/Ua.
Обычно цепь переменного тока включает в себя и активное сопротивление, и емкость, и индуктивность.
Полное сопротивление (Z) - это векторная сумма всех сопротивлений: активного, емкостного и индуктивного.
 - полное сопротивление цепи.
- полное сопротивление цепи.
Здесь:
 - активное сопротивление.
- активное сопротивление.
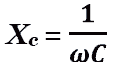 - емкостное сопротивление.
- емкостное сопротивление.
 - индуктивное сопротивление.
- индуктивное сопротивление.
 - полное сопротивление определяет силу тока в цепи по закону Ома.
- полное сопротивление определяет силу тока в цепи по закону Ома.
Угол сдвига фаз(Ток отстает от напряжения на 90 градусов) между напряжением и током в электрической цепи определяется аргументом ее комплексного сопротивления . Поэтому при анализе цепи часто бывает достаточно определить характер изменения этого угла при вариации некоторого параметра.
Комплексное сопротивление любого участка электрической цепи в общем случае имеет вещественную и мнимую составляющие Z = R + jX. Построим вектор Z на комплексной плоскости и проанализируем его поведение при вариации составляющих R и X.
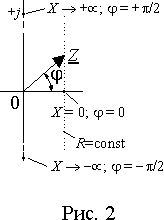 Пусть R= const, а X =var. Тогда конец вектора Z будет скользить по прямой R= const (рис. 2). При X = 0 сопротивление Z вещественное, т.е. чисто резистивное и сдвиг фаз между током и напряжением равен нулю.
Пусть R= const, а X =var. Тогда конец вектора Z будет скользить по прямой R= const (рис. 2). При X = 0 сопротивление Z вещественное, т.е. чисто резистивное и сдвиг фаз между током и напряжением равен нулю.
Если X , то вектор Z поворачивается в положительном направлении и его аргумент в пределе стремится к /2. Это означает, что пределом Z является комплексное индуктивное сопротивление.
При X , пределом вектора Z является бесконечно большое комплексное емкостное сопротивление.
Таким образом, изменение реактивного сопротивления в пределах < X < приводит к изменению угол сдвига фаз между током и напряжением в пределах /2 < < /2.
35. Энергетический процесс(вопрос 29 и 32) – ДОДЕЛАТЬ111
Мгновенная, активная, реактивная и полная мощности – Вопрос № 32
ТРЕУГОЛЬНИК МОЩНОСТЕЙ - графическое изображение активной, реактивной и полной мощностей в цепи переменного тока.

Треугольник мощностей получается из соотношения Р2 + Q2 = S2.
Коэффициентом мощности или cos φ электрической сети называется отношение активной мощности к полной мощности нагрузки расчетного участка.
cos φ = P/S, где:
· cos φ – коэффициент мощности;
· Р - активная мощность Вт;
· S - полная мощность ВА;
Коэффициент мощности можно определить как расчетным путем, так и измерить специальными приборами. Только в том случае, когда нагрузка имеет исключительно активный характер, cos φ равен единице. В основном же, активная мощность меньше полной и поэтому коэффициент мощности меньше единицы.
Следует учитывать, что низкий коэффициент мощности потребителя приводит:
· к необходимости увеличения полной мощности трансформаторов и электрических станций, а также к увеличению сечения питающих линий электропередач;
· к понижению коэффициента полезного действия вырабатывающих и трансформирующих элементов цепи;
· к увеличению потерь мощности и напряжения в проводах. При одних и тех же значениях мощности и напряжения уменьшение коэффициента мощности сопровождается увеличением тока в проводах, вследствие чего возрастают потери на нагрев, что, в свою очередь, приводит к падению напряжения в сети;
Чем меньше коэффициент мощности сети, тем менее загружена сеть активной мощностью и тем меньше коэффициент полезного действия использования сети. В связи с этим необходимо, чтобы как можно большую часть в полной мощности составляла именно активная мощность, а не реактивная, в этом случае коэффициент мощности будет ближе к единице.
Чтобы лучше понять данный вопрос, давайте рассмотрим причины низкого коэффициента мощности:
· Недогрузка асинхронных электродвигателей. Потребляемая активная мощность уменьшается пропорционально нагрузке, а реактивная мощность изменяется меньше;
· Неправильный выбор типа электродвигателя. Двигатели быстроходные и большой мощности имеют более высокий коэффициент мощности, чем тихоходные и маломощные;
· Повышение напряжения в сети. Ведет к увеличению намагничивающего тока индуктивных потребителей реактивной составляющей полного тока;
Для увеличения коэффициента мощности можно:
· изменить мощность и тип устанавливаемых электродвигателей;
· увеличить загрузку электродвигателей в процессе работы;
· уменьшить время работы в холостом режиме оборудования потребляющего индуктивную мощность;
· установить установку компенсации реактивной мощности с конденсаторами производства «Нюкон»;
36. В радиоэлектронных устройствах емкость является элементом колебательных контуров, фильтров, элементом связи между контурами и т. п. В силовых установках конденсаторы используют для улучшения коэффициента мощности, как элемент колебательного контура высокочастотных установок для закалки и плавки металлов. В любой электрической установке емкости образуются между проводами, проводами и землей и другими элементами токоведущих конструкций.
При большой протяженности проводов емкость может оказаться значительной, и при расчете цепей даже низкой, например промышленной, частоты ее необходимо учитывать. В высокочастотных цепях даже небольшие емкости оказывают существенное влияние на режим работы цепи и их необходимо учитывать.
Ток в цепи с емкостью (рис. 2.8, а) представляет собой движение зарядов к ее обкладкам:
(2.10)
i = dq/dt.
Выразив в (2.10) заряд q через емкость С и напряжение на емкости и С, из выражения
С = q/u С
получим
i = Cdu С /dt.
Напряжение на емкости изменяется синусоидально:
(2.11)
и = и С = U m sin ω t.
Тогда ток в цепи
| i = C | dU m sin ω t | . |
| dt |
Взяв производную, получим мгновенное значение тока в цепи с емкостью:
(2.12)
i = ω CU m cos ω t = I m sin (ω t + π/2).
Сравнивая выражения (2.11) и (2.12), можно сделать вывод, что ток в емкости опережает напряжение на емкости по фазе на 90°.
Векторная диаграмма цепи с емкостью приведена на рис. 2.8, б, а график мгновенных значений тока и напряжения — на рис. 2.8, в.

| Рис. 2.8. Электрическая цепь, содержащая емкостный элемент с емкостью С (а), ее векторная диаграмма (б) и графики мгновенных значений u, i, p (в) |
Напряжение и ток в цепи с емкостью, как следует из выражения (2.12), связаны соотношением
I m = ω CU m,
откуда
(2.13)
| I m = | U m | . |
| 1/ω C |
Разделив левую и правую части (2.13) на √2, получим закон Ома для цепи с емкостью:
(2.14)
| I = | U | = | U | , |
| 1/ω C | х С |
где х С = 1/ω C — емкостное сопротивление, Ом.
Таким образом, напряжение на емкости в цепи переменного тока может быть выражено через произведение тока на емкостное сопротивление:
U = U C = Iх C.
Мгновенное значение мощности р в цепи с емкостью равно произведению мгновенных значений напряжения и тока:
| Р = ui = U m sin ω tI m sin (ω t + π/2) = | U m I m | sin 2ω t = UI sin 2ω t = P m sin 2ω t. |
Из полученного выражения вытекает, что мгновенная мощность изменяется по закону синуса с частотой, в 2 раза большей частоты тока, и ее амплитудное значение
Р т = UI.
Среднее значение мощности за период (активная мощность), как видно из графика рис. 2.8, в, равно нулю:
| T | ||||
| P = | ∫ | ui dt = 0. | |||
Для пояснения энергетических процессов в цепях с емкостью воспользуемся графиками, изображенными на рис. 2.8, в. В первую четверть периода, в интервале времени между точками 1 и 2, напряжение на конденсаторе возрастает, происходит заряд конденсатора: электрическая энергия из сети поступает к конденсатору и накапливается в нем в виде энергии электрического поля. Накопленная энергия равна заштрихованной площади, ограниченной кривой р (t) (отмечена знаком «+»), и составляет
| T/4 | T/4 |
|
| ||||||||
| W C = | ∫ | ui dt = | ∫ | sin 2ω t dt = | . | ||||||
В следующую четверть периода, в интервале времени между точками 2 и 3, ток изменяет направление, а напряжение на конденсаторе убывает. Происходит разряд конденсатора: энергия электрического поля возвращается в сеть. Энергия, возвращенная в сеть, равна площади, ограниченной кривой р (t) (отмечена знаком «-»).
Из графиков рис. 2.8, в видно, что площади, определяющие запасенную и отданную энергии, равны. Следовательно, энергия, накопленная в электрическом поле емкости в первую четверть периода, полностью возвращается в сеть во вторую четверть периода.
В следующую четверть периода, в интервале времени между точками 3 и 4, изменяется полярность напряжения на обкладках конденсатора. Происходит заряд конденсатора: электрическая энергия из сети поступает к конденсатору и накапливается в нем в виде энергии электрического поля. В последнюю четверть периода, в интервале между точками 4 и 5, происходит разряд конденсатора: энергия электрического поля возвращается в сеть.
Таким образом, в цепи с емкостью, так же как и в цепи с индуктивностью, происходит непрерывный периодический процесс обмена энергией между сетью и конденсатором.
Изменение заряда на обкладках конденсатора при синусоидальном напряжении (конденсатор без потерь) - ДОДЕЛАТЬ111
Записать мгновенное значение тока, если задано его комплексное действующее значение  и синусоидальный закон изменения.
и синусоидальный закон изменения.

|
Решение. Для записи мгновенного значения необходимо определить амплитуду и начальную фазу тока. Длина вектора, проведенного из начала координат комплексной плоскости в точку, соответствующую комплексному числу, и называемого модулем, есть действующее значение тока
Максимальное (амплитудное) значение тока 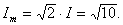 Угол i, образуемый вектором
Угол i, образуемый вектором  и положительным направлением вещественной оси, называемый аргументом комплексного числа – есть начальная фаза тока. Положительное направление отсчета углов – против часовой стрелки. Вектор тока расположен во второй четверти комплексной плоскости (вещественная часть тока – отрицательна, а мнимая – положительна).
и положительным направлением вещественной оси, называемый аргументом комплексного числа – есть начальная фаза тока. Положительное направление отсчета углов – против часовой стрелки. Вектор тока расположен во второй четверти комплексной плоскости (вещественная часть тока – отрицательна, а мнимая – положительна).
Угол, образуемый вектором с вещественной осью, определяется как арктангенс отношения мнимой части комплексного числа к вещественной. Поэтому начальная фаза тока
i=180-arctg(2/1)=180–6330'=11630':
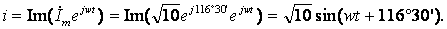
Таким образом, мгновенное значение тока
Временная и векторная диаграммы – Вопрос № 30
37. Рассмотрим RC-цепь, изображенную на рис. 3.20,а. Пусть на входе этой цепи действует напряжение u1(t).

Рис. 3.20. Дифференцирующие RC-(а) и RL-(б) цепи.
Тогда для этой цепи справедливо соотношение

и с учетом преобразований будем иметь
 (3.114)
(3.114)
Если для данного сигнала выбрать постоянную времени цепи τ=RC настолько большим, что вкладом второго члена правой части (3.114) можно пренебречь, то переменная составляющая напряжения uR≈u1. Это значит, что при больших постоянных времени напряжение на сопротивлении R повторяет входное напряжение. Такую цепь применяют тогда, когда необходимо передать изменения сигнала без передачи постоянной составляющей.
При очень малых значениях τ в (3.114) можно пренебречь первым слагаемым. Тогда
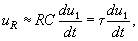 (3.115)
(3.115)
т. е. при малых постоянных времени τ RC-цепь (рис. 3.20,а) осуществляет дифференцирование входного сигнала, поэтому такую цепь называют дифференцирующей RC-цепью.
Аналогичными свойствами обладает и RL-цепь (рис. 3.20,б).

Рис. 3.21. Частотные (а) и переходная (б) характеристики дифференцирующих цепей.
Сигналы при прохождении через RС- и RL-цепи называют быстрыми, если
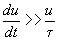 ,
,
или медленными, если
 .
.
Отсюда следует, что рассмотренная RC-цепь дифференцирует медленные и пропускает без искажения быстрые сигналы.
Для гармонической э. д. с. аналогичный результат легко получить, вычисляя коэффициент передачи цепи (рис. 3.20,а) как коэффициент передачи делителя напряжения со стационарными сопротивлениямиR и XC=1/ωC:
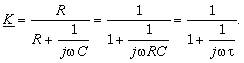 (3.116)
(3.116)
При малых τ, а именно когда τ<<1/ω, выражение (3.116) преобразуется в
 .
.
При этом фаза выходного напряжения (аргумент K) равна π/2. Сдвиг гармонического сигнала по фазе на π/2 эквивалентен его дифференцированию. При τ>>1/ω коэффициент передачи K≈1.
В общем случае модуль коэффициента передачи (3.116), или частотная характеристика цепи (рис. 3.20,а):
 (3.118)
(3.118)
а аргумент K, или фазовая характеристика этой цепи:
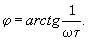 (3.119)
(3.119)
Эти зависимости показаны на рис. 3.21,а.
Такими же характеристиками обладает RL-цепь на рис. 3.20,б с постоянной времени τ=L/R.
Если в качестве выходного сигнала взять единичный скачок напряжения  , то интегрированием уравнения (3.114) можно получить переходную характеристику дифференцирующей цепи, или временную зависимость выходного сигнала при единичном скачке напряжения на входе:
, то интегрированием уравнения (3.114) можно получить переходную характеристику дифференцирующей цепи, или временную зависимость выходного сигнала при единичном скачке напряжения на входе:
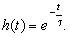 (3.120)
(3.120)
График переходной характеристики показан на рис. 3.21,б.
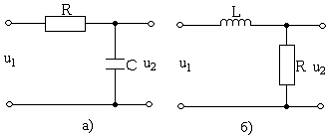
Рис. 3.22. Интегрииующие RC-(а) и LC-(б) цепи.
Рассмотрим RC-цепь, изображенную на рис. 3.22,а. Она описывается уравнением
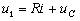
или
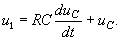 (3.121)
(3.121)
При малых τ=RC (для «медленных» сигналов) uC≈u1. Для «быстрых» сигналов напряжение u1 интегрируется:
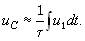 (3.122)
(3.122)
Поэтому RC-цепь, выходное напряжение которого снимается с емкости C называют интегрирующей цепью.
Коэффициент передачи интегрирующей цепи определяется выражением
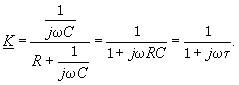 (3.123)
(3.123)
При ω<<1/τ K≈1.
Частотная и фазовая характеристики описываются соответственно выражениями
 (3.124)
(3.124)
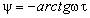 (3.125)
(3.125)
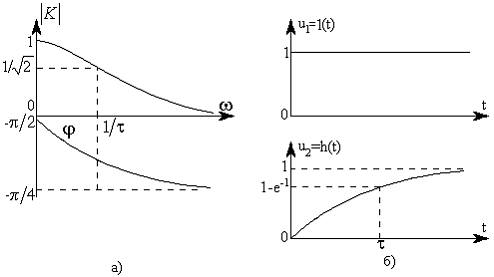
Рис. 3.23. Частотные (а) и переходная (б) характеристики интегрирующих цепей.
и изображены на рис. 3.23,а. Переходная характеристика (рис. 3.23,б) получается интегрированием (3.121) при  :
:
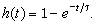 (3.126)
(3.126)
При равных постоянных времени такими же свойствами обладает RL-цепь, изображенная на рис. 3.22,б.
- Цепь синусоидального тока с емкостью – Вопрос № 36 и 39
Закон Ома для действующих и амплитудных значений тока и напряжения – Вопрос № 31 и 33
Ёмкостное сопротивление, его зависимость от частоты – Сопротивление, оказываемое конденсатором переменному току, зависит от величины емкости конденсатора и от частоты тока.
Чем больше емкость конденсатора, тем больший заряд переносится по цепи за время заряда и разряда конденсатора, а следовательно, и тем больший будет ток в цепи. Увеличение же тока в цепи свидетельствует о том, что уменьшилось ее сопротивление.
Следовательно, с увеличением емкости уменьшается сопротивление цепи переменному току.
Увеличение частоты тока увеличивает величину переносимого по цепи заряда, так как заряд (а равно и разряд) конденсатора должен произойти быстрее, чем при низкой частоте. В то же время увеличение величины переносимого в единицу времени заряда равносильно увеличению тока в цепи, а следовательно, уменьшению ее сопротивления.
Если же мы каким-либо способом будем постепенно уменьшать частоту переменного тока и сведем ток к постоянному, то сопротивление конденсатора, включенного в цепь, будет постепенно возрастать и станет бесконечно большим (разрыв цепи) к моменту появления в цепи постоянного тока.
Следовательно, с увеличением частоты уменьшается сопротивление конденсатора переменному току.
Подобно тому как сопротивление катушки переменному току называют индуктивным, сопротивление конденсатора принято называть емкостным.
Таким образом, емкостное сопротивление тем больше, чем меньше емкость цепи и частота питающего ее тока.
Емкостное сопротивление обозначается через Хс и измеряется в омах.
Зависимость емкостного сопротивления от частоты тока и емкости цепи определяется формулой Хс = 1/ωС, где ω — круговая частота, равная произведению 2πf, С—емкость цепи в фарадах.
Не нашли, что искали? Воспользуйтесь поиском: