Задачи для самостоятельного решения. 4.2. Проверьте, есть ли в заданной целочисленной последовательности a1 , a2 ,

4.1. Вычислите сумму Z = 1 + 2 + 3 +.... Вычисления прекратите, когда значение Z превысит заданное значение A.

4.2. Проверьте, есть ли в заданной целочисленной последовательности a1, a2,..., aN элементы, равные нулю. Если есть, найдите номер первого из них, если нет – выдайтесоответствующий текст.

4.3. Для заданного числа x вычислите первое из чисел последовательности sin x, sin sin x,

sin sin sin x,..., меньшее по модулю 10-2.

4.4. Выясните, имеются ли в заданном векторе A(N) два подряд идущих нулевых элемента.

4.5. Выясните, имеются ли в заданном целочисленном векторе A(N) три подряд идущих элемента одного знака.

4.6. Множество точек в пространстве задано своими целочисленными координатами. Определите, совпадает ли хотя бы одна из точек с началом координат.

4.7. Если у заданного вектора A(N) есть хотя бы один элемент, меньший, чем -5, то все отрицательные элементы замените их квадратами, оставив остальные элементы без изменения; в противном случае вектор домножьте на 0,1.

4.8. Имеется последовательность чисел a1, a2,..., aN. Найдите сумму первых из них (считая слева направо), произведение которых не превышает заданного числа М.

4.9. Задано целое A>1. Найдите наименьшее целое неотрицательное k, при котором 5 k > A.

4.10. Все элементы заданного вектора A(N), начиная с первого по порядку положительного

элемента, уменьшите на единицу.

4.11. Числа Фибоначчи (Fi) определяются по формулам

F 0 = F1 = 1; Fi = Fi-1 + Fi-2 при i = 2, 3,...

Найдите первое из чисел Фибоначчи, которое превосходит заданное число M (M>0).

4.12. Определите, имеются ли среди элементов побочной диагонали заданной целочисленной матрицы A(N, N) числа, равные нулю.

4.13. Найдите любое трёхзначные число, кратное заданному Р и не равное ему.

4.14. Вычислите приближённое значение бесконечной суммы:

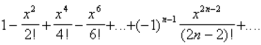
Суммирование производите до тех пор, пока очередное слагаемое не станет по абсолютной величине меньше заданного числа e>0.

4.15. Если в заданном целочисленном векторе A(N) есть элементы со значением, равным

заданному числу B, то переменной С присвойте значение, равное сумме всех элементов,

предшествующих первому по порядку такому элементу; в противном случае вывести соответствующий текст.

4.16. Дана последовательность из N целых чисел. Определите, со скольких положительных чисел она начинается.

4.17. Среди чисел

найдите номер и значение первого по порядку числа, абсолютная величина которого меньше заданного eps > 0. Если таких чисел нет, выведите на печать соответствуюший

текст.

4.18. Определите, имеется ли в заданном массиве A(N) хотя бы одна пара соседних чисел,

являющихся взаимнообратными.

4.19. Определите, выполняются ли для заданного вектора A(2N) условия:

а1 = а2N, a2 = a2N-1,..., aN = aN+1,

т.е. является ли он симметричным относительно своей середины.

4.20. Имеется монотонно убывающая последовательность чисел a1, a2,..., aN. Определите

квадрат суммы положительных членов этой последовательности.

4.21. Если в заданном целочисленном векторе A(N) есть элементы со значением, равным

заданному числу B, то переменной С присвойте значение, равное произведению всех элементов, следующих за первым по порядку таким элементом; в противном случае выведите соответствующий текст.

4.22. Определите, имеется ли в заданном целочисленном массиве X(N) число, кратное заданным числам А и В, и не кратное числу С.

4.23. Дано натуральное N. Выясните, сколько цифр оно содержит.

4.24. Найдите сумму цифр заданного натурального числа.

4.25. Цифры заданного натурального числа запишите в обратном порядке.

4.26. Проверьте, все ли элементы заданного массива A(N) положительны.

4.29. Найдите наименьший делитель заданного натурального числа A (не считая единицы).

4.28. Определите, является ли заданное натуральное число палиндромом (палиндром -

число, одинаково читаемое слева направо и справа налево).

4.29. Определите по данным музейного каталога, есть ли в музее хотя бы одна картина

Левитана или Шишкина. Если есть, выдайте ее название, в противном случае выдайте

соответствующий текст.

4.30. Определите по прейскуранту, можно ли подобрать в спортивном магазине велосипед, стоимость которого не превышает имеющуюся у покупателя сумму.

4.31. Известен начальный вклад клиента в банк и процент годового дохода. Определите,

через сколько лет вклад превысит заданный размер и каков при этом будет размер вклада.

4.32. Торговая фирма в первый день работы реализовала товаров на P тыс. руб., а затем ежедневно увеличивала выручку на 3%. Какой будет выручка фирмы в тот день, когда она

впервые превысит заданное значение Q? Сколько дней придется торговать фирме для достижения этого результата?

4.33. Малое предприятие в первый день работы выпустило P единиц товарной продукции.

Каждый последующий день оно выпускало продукции на Q единиц больше, чем в предыдущий. Сколько дней потребуется предприятию, чтобы общее количество выпущенной продукции за все время работы впервые превысило запланированный объем?

4.34. Определите, имеется ли в заданном множестве точек на плоскости хотя бы одна, принадлежащая заштрихованной на рисунке области (на рисунках даны окружности с единичным радиусом и парабола y=x2):

4.35. Даны два натуральных числа M и N - числитель и знаменатель дроби M / N. Требуется

сократить дробь, насколько это возможно.

4.36. На плоскости даны две точки А(2, 2) и В(2, 6), а также N точек со своими координатами. Определитe, есть ли среди этих N точек хотя бы одна, которая является:

а) вершиной равнобедренного треугольника с основанием АВ;

б) вершиной прямоугольного треугольника с катетом АВ.

4.37. Дано натуральное число N. Получите его запись в двоичной, восьмеричной и шестнадцатеричной системах счисления.

4.38. На соревнованиях по воздухоплаванию доля тепловых шаров от общего количества

шаров обычно составляет от 93,4% до 97,5% всех шаров. При каком наименьшем общем

количестве шаров возможно такое процентное соотношение?

4.39. По перечню редких и исчезающих видов животных и растений, содержащемуся в

"Красной Книге" вашего региона, определите, верно ли, что в нем содержится не менее

пяти подвидов папоротников и ни более двух подвидов фазанов.

4.40*. Городок состоит из N многоквартирных котеджей, расположенных вдоль прямой

дороги с одной ее стороны на равных расстояниях друг от друга. В городке проводят телефонную связь. Известно, сколько телефонных аппаратов надо установить в каждом доме. Определите, в каком из домов надо установить АТС, чтобы суммарное расстояние от АТС до всех телефонных аппаратов было минимальным. Если таких домов несколько, достаточно найти любой из них. Учтите, что каждый телефон связан с АТС отдельным

проводом.

4.41*. Вокруг считающего стоят N человек, один из которых назван первым, а остальные

занумерованы по часовой стрелке числами от 2 до N. Считающий ведет счет до М, начиная с первого. Человек, на котором остановился счет, выходит из круга. Счет возобновляется с человека, следовавшего за выбывшим, и так до тех пор, пока не останется один человек. Определите первоначальный номер последнего оставшегося человека. &nspb;

Не нашли, что искали? Воспользуйтесь поиском: