Принцип суперпозиции ЭСП. Поле элементарного диполя.

Принцип суперпозиции: напряжённость ЭСП, созданного системой зарядов равна векторной сумме напряжённостей полей, созданных каждым зарядом системы в отдельности.

Элементарный диполь – система двух равных по величине разноимённых зарядов, расстояния между которыми много меньше расстояний до точек пространства, в которых определяется поле этой системы.

Система характеризуется дипольным моментом, где 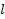– плечо диполя. Определим, используя принцип суперпозиции напряжённость ЭСП диполя на продолжении оси диполя.

Таким образом

В произвольной точке используется теорема косинусов. За берётся кратчайшее расстояние до оси диполя.

4 Теорема Гаусса для ЭСП в вакууме и ей применение к расчёту ЭСП.

Представляет собой один из методов расчёта ЭСП. Потоки ЭСП (вектора напряжённости) через называется:

Поток ЭСП через произвольную замкнутую поверхность:

Определим поток ЭСП точечного заряда через поверхность сферы радиуса , в центре которой – заряд :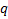

С другой стороны известно, что . Подставим.

Этот результат остаётся справедливым для поверхности формы. Действительно, геометрический смысл потока – число линий поля, пересекающих данную поверхность. Действительно, опишем около сферы поверхность произвольной формы.

Если заряд расположен вне замкнутой поверхности, то число линий поля, входящих в поверхность равно числу линий, выходящих из нее .

Теорема Гаусса. Поток ЭСП через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри поверхности, делёной на электрическую постоянную.

Замечание: если заряд расположен:

1. По объёму с объёмной плотностью –

2. По поверхности с поверхностной плотностью –

3. Вдоль линии с линейной плотностью –

Не нашли, что искали? Воспользуйтесь поиском: