Сопряжение острого и тупого углов.

И

3. Виды проецирования

Изображения предметов на чертежах получают проецированием. Проецирование - это процесс полу­чения изображения предмета на какой-либо поверх­ности Получившиеся при этом изображение называют проекцией предмета

Слово "проекция" в переводе с латинского означа­ет "бросание вперёд, вдаль". Нечто похожее на проекцию можно наблюдать, если параллельно стене, противопо­ложной окну, расположить ученическую тетрадь. На сте­не образуется тень в виде прямоугольника.

Элементами, с помощью которых осуществляется проецирование, являются (рис. 11): центр проецирова­ния - точка, из которой производится проецирование; объект проецирования - изображаемый предмет; плоскость проекции - плоскость, на которую производится проецирование; проецирующие лучи - воображаемые прямые, с помощью которых производится проецирова­ние, результатом проецирования является изображение, или проекция, объекта.

Различают центральное и параллельное проеци­рование. При центральном проецировании все проеци­рующие лучи исходят из одной точки - центра проеци­рования, находящегося на определённом расстоянии от плоскости проекций. На рис, 11а за центр проециро­вания условно взята электрическая лампочка. Исходящие от неё световые лучи, которые условно приняты за про­ецирующие, образуют на полу тень, аналогичную цен­тральной проекции предмета.

Метод центрального проецирования используется при построении перспективы. Перспектива даёт возмож­ность изображать предметы такими, какими они пред­ставляются нам в природе при рассмотрении их с опре­делённой точки наблюдения.

В машиностроительных чертежах центральные проекции не применяются. Ими пользуются в строитель­ном черчении и в рисовании.

При параллельном проецировании все проеци­рующие лучи параллельны между собой. На рис.11б по­казано, как получается параллельная косоугольная про­екция. Центр проецирования предполагается условно удалённым в бесконечность. Тогда параллельные лучи отбросят на плоскость проекций тень, которую можно принять за параллельную проекцию изображаемого предмета.

В черчении пользуются параллельными проекция­ми. Выполнять их проще, чем центральные.

Если проецирующие лучи составляют с плоскостью проекций примой угол, то такие параллельные проекции называются прямоугольными.

Прямоугольные проекции называют также ортого­нальными. Слово "ортогональный" происходит от гре­ческих слов "orthos" - прямой и "gonia" - угол. Чертежи в системе прямоугольных проекций дают достаточно полные сведения о форме и размерах предмета, так как предмет изображается с нескольких сторон. Поэтому в производственной практике пользуются чертежами, со­держащими одно, два, три или более изображений пред­мета, полученных в результате прямоугольного проеци­рования.

4. Масштабы

Для изображения на чертежах очень крупных или слишком мелких изделий (самолеты, часы) используют масштабы.
Масштаб — это отношение размеров изображения действительным размерам предмета.

Если изображения на чертежах имеют такие же размеры, как и действительные размеры детали, считается, что чертежи выполнены в натуральную величину, или в масштабе 1:1 (один к одному). Если изображения на чертеже имеют размеры больше действительных размеров детали, то для их построения использован масштаб увеличения. Если изображения на чертеже имеют размеры меньше действительных размеров детали, то для их построения использован масштаб уменьшения.

Стандарт (ГОСТ 2.302-68) устанавливает:

— масштаб натуральной величины — 1:1.
— масштабы уменьшения — 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1000.
— масштабы увеличения — 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1.

При любом масштабе на чертеже всегда наносят только действительные размеры. Масштаб записывают в специальной графе основной надписи по типу 1:1; 1:2; 2:1 и т. д. Масштаб может быть проставлен на поле чертежа только для тех изображений, которые выполнены в масштабе, отличном от масштаба, заявленного в основной надписи. В этом случае над изображением делают запись М 1:2; М 2:1 и т. д.

Сопоставьте изображения, выполненные в различных масштабах (рис. 56).

Чтобы построить чертеж детали в масштабе 2:1, необходимо линейные размеры изображения увеличить в два раза. Если необходимо выполнить изображение в масштабе 1:2, то линейные размеры уменьшаются в два раза. Размеры углов не изменяются при выборе масштаба изображения.

5. Линии чертежа

1. Сплошная толстая основная — применяется для выполнения линий видимого контура, линий контура сечений. Этой линией вы будете обводить внутреннюю рамку чертежа, графы основной надписи. Толщина сплошной основной линии (S) выбирается в пределах от 0,5 до 1,4 мм.
2. Сплошная тонкая линия предназначается для нанесения размерных и выносных линий, нанесения штриховки, проведения полок линий-выносок, для изображения воображаемых линий перехода одной поверхности в другую. Толщина линии выбирается от S/3 до S/2.
3. Сплошная волнистая линия применяется для изображения линии обрыва, разграничения вида и разреза. Толщина линии от S/3 до S/2. Этот тип линии выполняется от руки.
4. Сплошная тонкая с изломом. Этой линией изображают длинные линии обрыва. Толщина линии от S/3 до S/2.
5. Штриховая линия используется для изображения линий невидимого контура, невидимых линий перехода. Длину штриха выбирают от 2 до 8 мм, расстояние между штрихами от 1 до 2 мм. Толщина линии от S/3 до S/2.
6. Разомкнутая линия предназначается для изображения места секущей плоскости при построении сечений и разрезов. Толщина линии от S до 1,5 S.
7. Штрихпунктирная тонкая линия применяется для изображения осевых и центровых линий. Длина штриха выбирается от 5 до 30 мм, расстояние между штрихами от 3 до 5 мм. Штрихи чередуются с точками. Толщина линии от S/3 до S/2.
При изображении окружности штрихи штрихпунк-тирной линии должны пересекаться в центре окружности, и поэтому линию называют штрихпунктирная центровая, подчеркивая тем самым ее назначение (рис. 31).
Штрихпунктирная (осевая и центровая) линия должна выступать за контуры изображения предметов на 3-5 мм (рис. 31, а). Если необходимо задать центр окружности для отверстия диаметром менее 12 мм, то центровые линии выполняют одним штрихом (рис. 31, б). На рисунке 31 показано нанесение осевых и центровых линий.

8. Штрихпунктирная утолщенная линия применяется для изображения поверхности, подлежащей термообработке или покрытию (в школьном курсе не используется).
9. Штрихпунктирная тонкая линия с двумя точками применяется для изображения линий сгиба на развертках, для изображения частей изделий в крайних или промежуточных положениях. Длина штриха от 5 до 30 мм, расстояние между штрихами от 4 до 6 мм. Толщина линии от S/3 до S/2.

На рис. 32 представлен чертеж изделия, при выполнении которого использованы некоторые типы линий. Рассматривая его, обратите внимание на то, что:

1. Чертеж выполняется различными типами линий.
2. Толщина линий одного и того же типа на чертеже должна быть одинаковой.
3. Наименьшая толщина линий, выполненных в карандаше, должна быть 0,3 мм, а наименьшее расстояние между штрихами линий от 0,8 до 1,0 мм.
4. Штрихи, промежутки между штрихами для одного и того же типа линий должны быть приблизительно одинаковой длины.
5. Штрихпунктирная линия пересекается в центре окружностей штрихами и заканчивается изображением штриха.
6. Вычерчивание изображений предметов начинается с проведения осевых и центровых линий, от которых ведутся все последующие построения.

6. Способ замены плоскостей проекций.

Сущность этого способа заключается в том, что заменяют одну из плоскостей на новую плоскость, расположенную под любым углом к ней, но перпендикулярную к незаменяемой плоскости проекции. Новая плоскость должна быть выбрана так, чтобы по отношению к ней геометрическая фигура занимала положение, обеспечивающее получение проекций, в наибольшей степени удовлетворяющих требованиям условий решаемой задачи. Для решения одних задач достаточно заменить одну плоскость, но если это решение не обеспечивает требуемого расположения геометрической фигуры, можно провести замену двух плоскостей.

Применение этого способа характеризуется тем, что пространственное положение заданных элементов остается неизменным, а изменяется система плоскостей проекций, на которых строятся новые изображения геометрических образов. Дополнительные плоскости проекций вводятся таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задачи положений.

7. Форматы

ГОСТ 2.301-68 устанавливает форматы чертежной бумаги, предназначенной для выполнения чертежей и других конструкторских документов. Форматом называется размер листа бумаги (рис. 36). 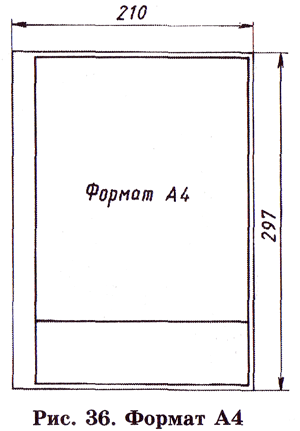На уроках черчения вы будете использовать лист формата А4 с размерами сторон 210X297 мм. По внешней рамке производится обрезка листа чертежной бумаги. Но если вы решили работать на бумаге, размеры которой чуть больше размера формата, то необходимо на нем выполнить сплошной тонкой линией внешнюю рамку (рис. 37). На формате проводится внутренняя рамка чертежа сплошной толстой основной линией на расстоянии 5 мм сверху, снизу, справа и 20 мм слева от внешней рамки. Левая сторона формата служит для подшивки чертежей. Пространство бумаги, ограниченное внутренней рамкой, называется полем чертежа

8. Способ вращения.

Способ вращения геометрической фигуры вокруг некоторой оси состоит в том, что фигура вращается вокруг оси до требуемого положения относительно заданной неподвижной системы плоскостей проекций.

В качестве оси вращения может быть взята любая прямая. В практике же преобразования комплексного чертежа широкое распространение получило вращение вокруг проецирующих прямых и линий уровня.

Рис. 6.1.

При вращении некоторой точки вокруг оси она описывает окружность, расположенную в плоскости, перпендикулярной оси вращения. На рис.6.1 рассмотрено вращение точки А вокруг горизонтально проецирующей оси. Плоскость вращения D параллельна плоскости П 1 и на фронтальной проекции изображается следом D 2. Горизонтальная проекция О 1 центра вращения О совпадает с проекцией M 1 N 1 оси, а горизонтальная проекция О 1 А 1радиуса вращения является его натуральной величиной. Вращаясь вокруг оси, точка А перемещается по окружности, которая на А 1 проецируется в окружность, а на П 2 - в отрезок прямой, параллельный оси х. На рис.6.1 поворот произведен на угол j против часовой стрелки так, чтобы в новом положении точки радиус вращения был параллелен плоскости П 2.

Если точку вращать вокруг оси, перпендикулярной плоскости П 2, то ее фронтальная проекция будет перемещаться по окружности, а горизонтальная - параллельно оси х.

Вращение вокруг проецирующей прямой применяют при решении задачи на определение натуральной величины отрезка прямой (рис.6.2). Ось вращения выбирают так, чтобы она проходила через одну из крайних точек отрезка, например, через точку В. Тогда при повороте точки А на угол j в положение А отрезок АВ перемещается в положение АВ, параллельное плоскости П 2. В этом случае отрезок будет проецироваться на П 2 в натуральную величину (½ В 2 А 2 ½= ½ ВА ½). Одновременно в натуральную величину будет проецироваться угол а наклона отрезка АВ к плоскости П 1.

Рис. 6.2.

Натуральную величину плоской фигуры удобнее находить с помощью вращения вокруг прямой уровня. Путем такого вращения плоскость, которой принадлежит рассматриваемая фигура, поворачивают в положение, параллельное плоскости проекций. При таком положении плоскости любая принадлежащая ей фигура будет проецироваться в натуральную величину.

Вращая плоскость вокруг горизонтали, можно перевести ее в положение, параллельное плоскости П 1. Вращение плоскости вокруг фронтали позволяет перевестиее в положение, параллельное плоскости П 2.

На рис.6.3 рассмотрено нахождение натуральной величины треугольника АВС при помощи вращения его вокруг горизонтали. Каждая точка плоскости треугольника АВС при вращении перемещается по окружности, перпендикулярной оси вращения. Так, точка В перемещается по окружности, плоскость D которой перпендикулярна горизонтали. Центр окружности О находится на оси вращения, а величина радиуса равна расстоянию от точки до оси вращения. Так как точка В вращается вокруг горизонтали, то окружность проецируется на П 1 в отрезок прямой, перпендикулярный горизонтали, а на П 2 - в эллипс, который можно не строить.

Рис. 6.3.

На рис.6.3 видно, что и на П 1, и на П 2 радиус вращения проецируется с искажением. Натуральную величину радиуса находим методом прямоугольного треугольника (см. свойство ортогонального проецирования). Для этого принимаем горизонтальную проекцию О 1 В 1 за катет прямоугольного треугольника. Второй катет должен быть равен разности координат Z концов отрезка OB (Z В - Z 0). Гипотенуза треугольника О 1 В 1 В 1' (О 1 В 1') равна R. После поворота плоскость треугольника будет параллельна П 1. Следовательно, 0В спроецируется на П 1 в натуральную величину. Горизонтальную проекцию нового, после поворота, положения точки В (В 1') находим на пересечении дуги окружности, проведенной из горизонтальной проекции центра вращения О 1, радиусом, равным О 1 В 1, с горизонтальной проекцией плоскости A (А 1).

Точка С также перемещается по окружности, плоскость которой Г перпендикулярна горизонтали. Точка 1 находится на горизонтали, поэтому при вращении не перемещается. Так как точки В, 1 и С находятся на одной прямой, то горизонтальную проекцию нового, после поворота, положения точки С найдем на пересечении прямой, проведенной через В 1 и 1 1, с горизонтальной проекцией плоскости Г (Г 1).

9. Аксонометрия. Сущность метода и основные понятия.

10. Стандартные аксонометрические проекции.

Виды стандартных аксонометрических проекций

На практике наибольшее применение нашли прямоугольные аксонометрические проекции, из которых стандартизованы изометрическая и диметрическая

проекции, отличающиеся друг от друга расположением предмета относительно плоскости проекций П1 (ГОСТ 2.317-69). На рис. 30, а и б показано положение аксонометрических осей х', y', z'.

Рис. 30. Положение аксонометрических осей:

а – в изометрии; б – в диметрии

Для упрощения построений изометрическую проекцию выполняют без искажения по осям х', у', z', приняв коэффициент искажения равным 1. Диметрию выполняют без искажения по осям х' и z' и с коэффициентом искажения, равным 0,5, по оси у'. При этом изометрическая проекция получается увеличенной в 1,22 раза, а диметрическая – в 1,06 раза. На рис. 31, а и б показаны изображения детали в изометрии и диметрии для сравнения.

Рис. 31. Изображение детали:

а – в изометрии; б – в диметрии

В разновидностях аксонометрических проекций отсутствуют перспективные искажения, вследствие чего изображение получается условным и простым. Ф

11. Чертежный шрифт. Правила нанесения размеров на чертеже.

Стандарт устанавливает десять размеров шрифта: 1,8; 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40. За размер шрифта принимается величина, определяющая высоту прописной (заглавной) буквы. Шрифт может быть выполнен как с наклоном в 75°, так и без наклона.

Начертание букв чертежного шрифта. Высота буквы измеряется перпендикулярно к основанию строки.
Прописные буквы. Высота прописной буквы (h) равна размеру шрифта. Нижние элементы букв Д, Ц, Щ и верхний элемент буквы Й выполняются за счет расстояний между строками. Толщину линии шрифта (d) выбирают равной 0,1 h. Используя названные параметры (h, 0,lh), выстраивают вспомогательную сетку, в которую вписывают буквы (рис. 26).

Ширина большинства прописных букв (g) равна 0,6h или 6d, что примерно соответствует размеру h ближайшего наименьшего номера шрифта. Исключение составляют буквы А, Д, М, X, Ц, Ы, Ю, ширина которых равна 0,7d, ширина букв Ж, Ф, Щ, Ш, Ъ принимается за 0,8d, а ширина букв Г, 3, С составляет 0,5d. Написание прописных букв дано на рис. 26.

Строчные буквы. Высота большинства строчных букв (с) равна 0,7h, что примерно соответствует размеру (h) ближайшего наименьшего номера шрифта. Например, для шрифта № 10 высота строчной буквы будет равна 7 мм, а для размера № 7 — 5 мм. Верхние и нижние элементы строчных букв выполняются за счет расстояний между строками и выходят на величину 3d (рис. 27).

Ширина большинства строчных букв равна 5d. Ширина букв а, м, ц, ъ равна 6d, букв ж, т, ф, ш, щ, ы, ю — 7d, а букв з, с — 4d.

При написании букв пользуйтесь таблицей 1, в которой даны расчеты параметров шрифта.

Рассмотрев написание букв чертежного шрифта (рис. 26, 27), нетрудно заметить, что 16 прописных и строчных букв русского алфавита имеют одинаковое начертание. Написание других прописных букв отличается от написания строчных. Начертание цифр и знаков чертежного шрифта представлено на рис. 28.

На начальной стадии овладения навыком написания чертежным шрифтом следует писать по вспомогательной сетке и только потом переходить к свободному письму с использованием строки, состоящей из двух параллельных линий, проведенных друг от друга на расстоянии высоты прописной или строчной буквы.

При написании чертежного шрифта следует усвоить следующие правила:

1. Все надписи на чертеже должны быть выполнены от руки.
2. Высота букв, цифр и знаков на чертежах должна быть не менее 3,5 мм.
3. Начертание букв выполняйте по частям. Движение руки при выполнении прямолинейных элементов букв осуществляется сверху вниз или слева направо, а закругленных — движением вниз и влево или вниз и вправо. Стрелка указывает направление движения рук (рис. 29).
4. Одинаковые элементы различных букв, цифр, знаков следует выполнять одним и тем же приемом, что способствует выработке автоматизма при их написании.
5. Выдерживайте заданный наклон шрифта с помощью направляющих штрихов.
6. Строго соблюдайте конструкцию каждой буквы и соотношение высоты и ширины буквы, используя таблицу 1.
7. Старайтесь выдерживать такое расстояние между буквами, чтобы зрительно оно казалось одинаковым.
8. Четкость, ясность и удобство чтения чертежа зависят от качества его выполнения и правильного выбора размеров шрифта.
9. Все надписи на чертеже должны быть аккуратными.

12. Сопряжения

Плавный переход одной линии в другую называется сопряжением. Общая для сопрягаемых линий точка называется точкой сопряжения, или точкой перехода. Для построения сопряжений надо найти центр сопряжения и точки сопряжений. Рассмотрим различные типы сопряжений.

Сопряжение прямого угла. Пусть необходимо выполнить сопряжение прямого угла радиусом сопряжения, равным отрезку АВ (R=AB). Найдем точки сопряжения. Для этого поставим ножку циркуля в вершину угла и раствором циркуля, равным отрезку АВ, сделаем засечки на сторонах угла. Полученные точки а и b являются точками сопряжения. Найдем центр сопряжения — точку, равноудаленную от сторон угла. Раствором циркуля, равным радиусу сопряжения, из точек а и b проведем внутри угла две дуги до пересечения друг с другом. Полученная точка О — центр сопряжения. Из центра сопряжения описываем дугу заданного радиуса от точки а до точки Ь. Обводим вначале дугу, а затем прямые линии (рис. 70).

Сопряжение острого и тупого углов.

Чтобы построить сопряжение острого угла, возьмем раствор циркуля, равный заданному радиусу R=AB. Поочередно поставим ножку циркуля в двепроизвольные точки на каждой из сторон острого углса. Проведем четыре дуги внутри угла, жак показано на ргас. 71, а. К ним проведем две касательные до пересечения в точке О — центре сопряжения (рис. 71, б)- Из центра сопряжения опустим перпендикуляры на стороны угла. Полученные точки а и b будут точками сопряжения (рис. 71, б). Поставив ножку циркуля в центр сопряжения (О), раствором циркуля, равным заданному радиусу сопряжения (R=AB), проведем дугу сопряжения.

Аналогично построению сопряжения острого угла строят сопряжение (скругление) тупого угла.

Не нашли, что искали? Воспользуйтесь поиском: