Загальне поняття сер величин

СВ - показники які дають узагальнюючу ха-ку статистичним сукупностям однотипних явищ по варіаційній ознаці

Типи:

обємні (арифметична, геометрична, квадратична)

структурні (мода медіана)

Арифметичн а проста використовується коли кожна варіанта сукурності зустрічається один раз (Х^-- =Ʃх/n)

Зважена арифм використовуэться коли варыанти сукупносты зустрычаються не 1 раз (Х^-- =Ʃхi*ni/Ʃni)

Характер первинних даних
індивідуальні значення	згруповані дані
Середня арифметична (k = 1)
проста –	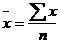зважена – f=x
Середня гармонійна (k = –1)
проста –	зважена – z=w
Середня квадратична (k = 2)
проста –	зважена – f=n

Геометрична проста: Хсер=X1*X2*…*Xn под коренем н-го степеня

Хронологічна використ коли дані в конктретний момент часу

33. Види середніх величин

За назвами в статистиці використовуються середня арифметична, середня хронологічна, середня геометрична, середня квадратична величини, середня гармонічна. Зміна значення показника степенної середньої величини (k) визначає вид середньої величини:

якщо k = 1, то ми одержуємо середню арифметичну величину;

якщо k = 2, то одержуємо середню квадратичну;

якщо k = 3, то – середню кубічну;

якщо k = - 1,– маємо середню гармонічну;

якщо m = 0, то середню геометричну.

З степенних середніх в правовій статистиці найчастіше використовують середню арифметичну, значно рідше – середню гармонічну; середня геометрична застосовується лише при обчисленні середніх темпів динаміки, а середня квадратична – при обчисленні показників варіації.

34. Властивості середньої (математичні).

1)aлгебраїчна сума відхилень всіх варіант від середньої дорівнює 0:

2) Якщо одну із варіант збільшити або зменшити на певну величину, то і середня зміниться на таку ж величину:

3) Якщо кожну варіанту розділити чи помножити на довільне число, то і середня збільшиться або зменшиться на те ж саме число

4) Якщо частоти всіх варіант помножити чи поділити на довільне число, то середня не зміниться

5) Сума квадратів відхилень варіант від середньої менша за будь-яку іншу величину

35. Середні структурні

До середніх структурних відносяться дві величини, які називаються "мода" і "медіана".Структурні величини мода і медіана застосовуються для вивчення внутрішньої будови рядів розподілу, тобто їх структури.

36. Середня гармонійна

Середня гармонійна величина використовується у тому випадку, якщо відомі обернені значення осереднюваного показника.
Середня гармонічна — це обернена до середньої арифметичної із обернених значень ознак. її обчислюють, коли необхідно осереднення обернених індивідуальних значень ознак шляхом їх підсумування (наприклад, у випадках визначення середніх витрат часу, праці, матеріалів на одиницю продукції тощо). У випадку розрахунку середньої гармонічної зваженої її обчислюють тоді, коли відомі дані про загальний обсяг ознаки (z = xf), а також індивідуальні значення ознаки (х), невідома є частота (f). Формули середньої гармонічної - простої і зваженої — мають такий вигляд:

- для простої: Хсер = n / ∑1 / x

- для зваженої: Хсер =∑z / ∑z / x

Не нашли, что искали? Воспользуйтесь поиском: