
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Середня арифметична
Середня арифметична - це найпоширеніший вид середньої між інших. Вона застосовується тоді, коли відомі індивідуальні значення усереднюваної ознаки та їх кількість у сукупності. Тоді проста середня арифметична обчислюється діленням загального обсягу значень ознаки на обсяг сукупності:
Хсер = (x1 + x2 + … + xn) / n = ∑x / n
38. Мода:сутність,методика визначення
Мода (М0) — це значення ознаки, що найчастіше зустрічається у сукупності. Таким чином, у дискретному ряді розподілу - це варіанта, що має найбільшу частоту. В інтервальному ряді розподілу мода знаходиться за формулою:

де: хмо — нижня межа модального інтервалу;
і — величина модального інтервалу;
f2, f1, f3 — відповідно частота модального, передмодального та після модального інтервалів
39. Медіана:сутність,методика визначення
Медіана (Ме) — це значення ознаки, що ділить рангований ряд значень показника на дві рівні частини. У першої половини одиниць значення ознаки менше медіани, а у другої — більше. Тобто, медіана — це серединне значення

40.Поняття варіації,показники варіації
Варіацією в статистиці називають кількісні зміни величини досліджуваної ознаки в межах однорідної сукупності, які зумовлені впливом дії різних факторів.
Показники
· розмах варіації становить різницю між мінімальним і максимальним значенням ознаки: R = xmax – xmin.
· Середнє лінійне відхилення являє собою середню арифметичну з абсолютних значень відхилень окремих варіант від середньої арифметичної.

· Дисперсією називають середній квадрат відхилень індивідуальних значень ознаки від середньої арифметичної. її визначають за формулами:

· Середнє квадратичне відхилення одержують шляхом добування кореня квадратного з дисперсії:

· Коефіцієнт варіації

41.Статистичні методи вивчення взаємозв’язків
Види взаємозв’язків між явищами та процесами.
Балансовий та графічний методи.
Балансовий метод вивчення взаємозв’язків застосовується для системи показників, між якими існує балансовий зв’язок
Графічний метод передбачає зображення взаємозв’язку між двома ознаками у вигляді лінії або сукупності крапок. Цей метод дає наочне уявлення про характер взаємозв’язку і найчастіше використовується на початку дослідженні для формування певної гіпотези
Метод порівняння паралельних рядів даних.
Для вивчення стохастичних (кореляційних) зв'язків використовується метод порівняння паралельних рядів двох показників, один з яких є факторним (Х), а другий – результативним (Y). При цьому основним завданням застосування цього методу є оцінка тісноти (сили) взаємозв'язку та визначення його напрямку на основі розрахунку спеціальних коефіцієнтів.
Метод аналітичного групування.
Метод аналітичного групування полягає у тому, що сукупність розбивається на групи за факторною ознакою (Х), далі по кожній групі та по сукупності визначаються середні значення Х та Y. Порівняння середній значень факторної та результативної ознак дозволяє зробити певні висновки про наявність та напрямок взаємозв'язку між ними
Парний кореляційно-регресійний аналіз.
Стохастичні зв'язки, котрі характеризуються взаємодією середніх значень факторної та результативної ознак, називаються кореляційно-регресійними. Такі зв'язки досліджуються з допомогою кореляційно-регресійного аналізу.Найважливішою характеристикою кореляційного зв'язку є ліній регресії, тобто функція, котра пов'язує середні значення Х та Y. Кореляційно-регресійна модель взаємозв'язку являє собою рівняння регресії
Множинна регресія і кореляція.
Як відомо, більшість соціально-економічних показників формується під впливом не одного, а багатьох факторів. Метод побудови моделі такого зв'язку має назву багатофакторного кореляційно-регресійного аналізу. В цьому випадку результативна ознака (Y) пов'язується з допомогою рівняння множинної регресії з двома або більше факторними ознаками (Х1, Х2, Х3,..., Хm).Найважливішими умовами побудови багатофакторної моделі зв'язку є достатня кількість одиниць у сукупності (як мінімум у 8 разів більше, ніж число факторів) та відсутність мультиколінеарності факторів (близького до функціонального зв'язку між ними). В тому випадку, якщо два факторних показники мультиколінеарні, один з них повинен бути виключений з моделі.
Оцінка тісноти взаємозв’язку між атрибутивними ознаками.
Для аналізу взаємозв'язку між атрибутивними ознаками будуються спеціальні таблиці, що мають назву таблиць співзалежності. В тому випадку, коли утворюються по дві групи за факторною та результативною ознаками, або коли вони є альтернативними,
42. Види взаємозв’язків соціально-економічних явищ
Розрізняють два типи зв’язків — функціональні та стохастичні. У разі функціонального зв’язку кожному значенню фактора х відповідає одне або кілька чітко визначених значень у. Такою, наприклад, є залежність довжини ртутного стовпчика від температури навколишнього середовища. Знаючи х, можна в кожному окремому випадку точно визначити результат у.
У соціально-економічних науках до функціонального типу належать зв’язки між показниками — адитивні (a + b + c) або мультиплікативні (a = bc, c = a/b), а також залежність середніх величин від структури сукупност
Стохастичні зв’язки виявляються як узгодженість варіації двох чи більше ознак. У ланці зв’язку «х у» кожному значенню ознаки х відповідає певна множина значень ознаки у, які утворюють так званий умовний розподіл.
43.суть і завдання дисперсійного аналізу
Дисперсійний аналіз - це метод статистичної оцінки надійності проявлення залежності результативної ознаки від одного або кількох факторів. За допомогою методу дисперсійного аналізу проводиться перевірка статистичних гіпотез відносно середніх в кількох генеральних сукупностях, які мають нормальний розподіл.
За допомогою дисперсійного аналізу вирішуються три основних завдання: 1) загальна оцінка істотності відмінностей між груповими середніми; 2) оцінка вірогідності взаємодії факторів; 3) оцінка істотності відмінностей між парами середніх.
44. Принципова схема дисперсійного аналізу
Принципова схема дисперсійного аналізу включає встановлення основних джерел варіювання результативної ознаки і визначення обсягів варіації (сум квадратів відхилень) за джерелами її утворення; визначення числа ступенів свободи, що відповідають компонентам загальної варіації; обчислення дисперсій як відношення відповідних обсягів варіації до їх числа ступенів свободи; аналіз співвідношень між дисперсіями; оцінка вірогідності різниці між середніми і формулювання висновків.
Зазначена схема зберігається як при простих моделях дисперсійного аналізу, коли дані групуються за однією ознакою, так і при складних моделях, коли дані групуються за двома і більшим числом ознак. Однак із збільшенням числа групувальних ознак ускладнюється процес розкладання загальної варіації за джерелами її утворення.
Відповідно до принципової схеми дисперсійний аналіз можна подати у вигляді п'яти послідовно виконуваних етапів:
1) визначення і розкладання варіації;
2) визначення числа ступенів свободи варіації;
3) обчислення дисперсій та їх співвідношень;
4) аналіз дисперсій та їх співвідношень;
5) оцінка вірогідності різниці між середніми і формулювання висновків з перевірки нульової гіпотези.
45. Алгоритм одно факторного аналізу дисперсійного аналізу
Виходячи з передумов, коректний алгоритм однофакторного дисперсійного аналізу за Фішером має складатися з наступних етапів.
1. Перевірка стат. гіпотези щодо нормальності вибірок.
2. Перевірка стат. гіпотези щодо однорідності дисперсій вибірок.
3. Розрахунок загальної, факторної та залишкової дисперсії.
4.Обчислення спостережуваного значення критерію Фішера.
5. Обчислення критичного значення критерію Фішера
46. Алгоритм дво факторного аналізу дисперсійного аналізу
Дисперсійний двофакторний аналіз застосовується в тих випадках, коли досліджується одночасна дія двох факторів на різні вибірки об'єктів, тобто коли різні вибірки опиняються під впливом різних поєднань двох факторів. Може статися, що одна змінна значущо діє на досліджувану ознаку тільки при певних значеннях іншої змінної. Наприклад, посилення мотивації може підвищувати швидкість рішення завдань у високоінтелектуальних осіб і знижувати її у низькоінтелектуальних. Отже, дисперсійний двофакторний аналіз дозволяє оцінити не лише вплив кожного з факторів, але й їхню взаємодію.
Суть методу залишається тією самою, як і при однофакторній моделі, але у двофакторному дисперсійному аналізі можна перевірити більшу кількість гіпотез, проте розрахунки дещо складніші, ніж в однофакторних комплексах.
Алгоритим
1. Формулювання гіпотез.
2. Розрахунки критеріїв
3. Розрахувати середні значення
4. Розрахувати суми квадратів різниць
5. Розрахувати середні квадрати
6. Розрахувати емпіричні критерії
7. Критичні значення
8. Прийняття рішення.
9. Формулювання висновків
47. Загальне поняття кореляційно-регресійного аналізу
Кореляційний зв’язок – частиний випадок стохастичного при якому зміна середнього значення результативної ознаки обумовлена зміною факторної ознаки.
Кореляція (лат. взаємозв’язок) – це статистична залежність між випадковими величинами, що не має строгого функціонального характеру, але при якій зміна однієї випадкової величини приводить до зміни математичного очікування іншої.
Розрізняють такі види кореляційного зв’язку:
1) Парна кореляція – взаємозв’язок між двома випадковими величинами.
2) Множинна кореляція – залежність результативної ознаки від двох і більш факторних.
3) Частинна кореляція – залежність між результативною і факторною ознаками при фіксованому значенні інших факторних ознак.
Можна розглядати два види аналізу між змінними: кореляційний та регресійний аналіз. Кореляційний аналіз досліджує щільність зв’язку між результативною та факторною ознаками, а регресійний – форму зв’язку (тобто аналітичний вираз зв’язку). Тобто основною його ціллю є оцінка функціональної залежності середнього значення результативної ознаки від значення факторної х.
Умовами застосування кореляційно-регресійного аналізу є:
1) Всі ознаки та їх сумісні розподіли підпорядковуються нормальному закону.
2) Дисперсія результативної ознаки є постійною (D(y)=const) при зміні як її величини при зміні величини факторної (умова гомоскедастичності).
3) Окремі спостереження повинні бути незалежними.
Розмірність рівняння регресії (кількості факторів) існує такий емпіричний критерій: кількість факторних ознак (k) в 5–6 разів менше об’єму вибірки (n)
В теорії кореляційно-регресійного аналізу розрізняють такі моделі:
1. Відносно кількості змінних: проста і множинна, або багатофакторна регресія (кореляція).
2. Відносно форми зв’язку: лінійна і нелінійна.
48.Вимірювання тісноти зв’язку між корелюючи ми ознаками
Щоб виміряти тісноту прямолінійною зв'язку між двома ознаками, користуються парним коефіцієнтом кореляції, який позначається r.
Так як при кореляційного зв'язку мають справу не з приростом функції у зв'язку зі зміною аргументу, а з сполученої варіацією результативних і факторних ознак, то визначення тісноти зв'язку, по суті, зводиться до вивчення цієї пов'язаності, тобто того, якою мірою відхилення від середнього рівня однієї ознаки пов'язане з відхиленням іншого. Це означає, що при наявності повної прямого зв'язку всі значення (х-X) і (у-Y) повинні мати однакові знаки, при повній зворотної - різні, при частковій зв'язку знаки в переважній кількості випадків будуть збігатися, а при відсутності зв'язку - збігатися приблизно в рівному числі випадків.
Для оцінки суттєвості коефіцієнта кореляції користуються спеціально розробленої таблицею критичних значень r.
49.Однофакторна прямолінійна кореляція.
50.Множинна кореляція.
Методи вимірювання кореляційного зв'язку одночасно між двома, трьома і більше кореляційними ознаками створюють вчення про множинну кореляцію. У моделях множинної кореляції залежна змінна «У» розглядається як функція кількох (у загальному випадку n) незалежних змінних «х».
Припущення про наявність лінійного зв'язку рівняння множинної регресії може бути показано в такому вигляді:

51.Побудова рівнянь кореляційного зв’язку.
Кореляційно-регресійний аналіз складається з таких етапів:
· попередній (апріорний) аналіз,
· збирання інформації та її первинна обробка,
· побудова моделі (рівняння регресії),
· оцінка й аналіз моделі.
52.Рівняння регресії, визначення його параметрів.
Рівняння, що відображує зміну середньої величини однієї ознаки (у) в залежності від другої (х), називається рівнянням регресії або рівнянням кореляційного зв'язку.
При простій кореляції це рівняння має вигляд: Уі =а0 +а1Х,
де у' ~ середнє теоретичне значення у при даному значенні х; a^1- параметри рівняння.
Кореляційне рівняння пов'язує результативну ознаку з факторною у вигляді рівняння прямої лінії, де параметр визначає
середню зміну результативної ознаки (у) при зміні факторної ознаки (х) на одиницю її натурального виміру.
Невідомі параметри ^0 і aI знаходять за способом найменших квадратів, який ставить умову, щоб сума квадратів відхилень у від
аплікат у*, обчислених за рівнянням регресії, була найменшою, або, інакше кажучі, щоб при зображенні в прямокутній системі координат теоретична лінія регресії проходила б максимально близько до фактичних даних. Такій умові відповідає пряма, параметри якої є коренями системи нормальних рівнянь: 
|
53.Економічна оцінка коефіцієнтів: кореляції, регресії, детермінації.
Коефіцієнт кореляції – показник, який використовують для вимірювання щільності зв'язку між результативними і факторними ознаками у кореляційно-регресійній моделі за лінійної залежності. За абсолютною величиною коефіцієнту кореляції коливається в межах від -1 до +1. Чим ближчий цей показник до 0, тим менший зв'язок, чим ближчий він до ±1 – тим зв'язок тісніший. Знак «плюс» при коефіцієнті кореляції означає прямий зв'язок між ознаками х і у, знак «мінус» – обернений. 
54.Криволінійна кореляція.
При криволінійній формі зв'язку збільшення факторної ознаки призводить до нерівномірного збільшення (або зменшення) результативної ознаки, або ж зростання її величини змінюється спаданням, а зменшення - збільшенням.
Для визначення зв'язку між ознаками, взаємовідношення яких передбачає можливість існування оптимальних розмірів операцій, використовують рівняння параболи:
ух = а0 + OL1X + аг х.
Одна з особливостей цього типу кривої та, що вона завжди має точку перетину (критичну точку), яка характеризує оптимальний варіант розміру величини результативної ознаки, і змінює напрямок свого руху лише один раз. Якщо в рівнянні величина a^ виражена від'ємним числом, а а2- додатним, то крива змінюватиме напрямок спаду на зростання.
Для розрахунку параметрів рівняння параболи другого порядку використовується така гигтемя нппмяпьних піинянь:

|
55.Ряди динаміки: поняття, види.
Ряди динаміки – це ряд розташованих у хонологічному порядку значень показника, які характеризують зміни величини досліджуваного явища у часі.
Класифікація рядів динаміки: 1) спосіб вираження досліджуваних показників(абсолютних, відносних, середніх величин); 2) охоплення явища у часі(моментні, інтервальні); 3) повнота охоплення періодів часу(повні, неповні).
56.Правила побудови динамічних рядів.
1.показники ряду динаміки повинні бути достовірними, точними науково обґрунтованими. 2. Показники РД повинні бути співставлені за методологією. 3. Спів ставність рівнів ряду за періодами часу. 4. Спів ставність показників динаміки за колом досліджуваних об’єктів. 5. Спів ставність показників за територією.
57.Аналітичні показники ряду динаміки.
Абсолютний приріст (А) - це абсолютна величина розміру змін досліджуваного явища, характеризується вона різницею між двома рівнями ряду динаміки. еличина абсолютного приросту показує на скільки одиниць рівень одного періоду більше або менше будь - якого іншого (як правило, попереднього) періоду, а отже він може мати знак "+" чи <<-".Б. А= Yn- Y0. Л. Yn- Yn-1.
Коефіцієнт зростання (К)- це відношення наступного рівня до базисного або попереднього. Він показує, у скільки разів рівень даного періоду більше або менше будь - якого рівня, прийнятого за базу порівняння. Коефіцієнт зростання, виражений у відсотках, називають темпом зростання. Залежно від мети дослідження за базу порівняння може прийматися постійний для всіх рівень ряду або кожний той, що передує йому. Б.с. К= Yn /Y0/ Л.с. К= Yn/ Yn-1.
Темп зростання – це коефіцієнт виражений у %. Тзр=К*100. Це відносна величина динаміки.
Темп приросту – показує на скільки % рівеь явища збільшилась або зменшилась за базу порівняння. Тпр=Тзр-100.
Абсолютне значення 1% приросту являє собою частку від ділення абсолютного приросту на відповідний показник темпу
приросту: n=Yn-1/100
Дана величина являє собою соту частину попереднього рівня
58. Середні характеристики аналітичних показників ряду динаміки.
В інтервальному ряді з рівними інтервалами часу застосовують середню арифметичну прост у:  .
.
У моментних динамічних рядах з рівними проміжками між датами середній рівень обчислюється за формулою середньої хронологічної: 
Середній рівень абсолютного приросту визначають за формулою середньої арифметичної простої з ланцюгових приростів: 
Середній коефіцієнт зростання обчислюється за формулою середньої геометричної з індивідуальних ланцюгових коефіцієнтів зростання: 
Середній темп зростання – це середній коефіцієнт виражений у %. 
Середній темп приросту – це різниця між середнім темпом зростання і 100.
59. Поняття тенденції рядів динаміки.
Тенденція – певний напрям розвитку, який набуває плавної траєкторії. У РД її описують за допомогою функції  , де t – змінна часу(0..n),
, де t – змінна часу(0..n),  - теоретичні рівні ряду. Тенденція – це основний напрямок розвитку, який характеризується достатньо стійку зміну явища у часі, відносно вільну від випадкових коливань.
- теоретичні рівні ряду. Тенденція – це основний напрямок розвитку, який характеризується достатньо стійку зміну явища у часі, відносно вільну від випадкових коливань.
60.Аналітичне вирівнювання рядів динаміки.
прийоми вирівнювання динамічних рядів: змикання ряду динаміки застосовують, коли явища за деякими ознаками є неспівставними. Неспівставність може бути наслідком територіальних знім. В цьому випадку визначають коефіцієнт зімкнення ДР Кз=Ун/Ус. Приведення рівнів ряду динаміки до однієї основи використовують, коли виникає потреба порівняти зміну динамічних рядів кількох споріднених або взаємопов’язаних явищ для цього абсолютні показники перетворюють у відносні, прийнявши ріві будь-якого періоду за 1 або 100%. Інтер-, екстраполяція. інтерполяція – це знаходження невідомого або відсутнього рівня ДР в середині періодів дослідження. Екстраполяція – розрахунок показників, які можуть знаходитися за межами досліджуваного явищаю
61.Вивчення сезонності.
Сезонність – це негативне явище, яке обумовлює нерівномірність виробничих процесів та негативно позначається на використанні робочої сили.
Для вивчення сезонності використовують показники варіації: 1) амплітуда коливань: R=Ymax-Ymin. 2) середнє лінійне відхилення d= 
3)середня квадратичне відхилення  . Коефіцієнт сезонності – це відношення показника за звітний період до його середньорічного значення Кс=Yn/
. Коефіцієнт сезонності – це відношення показника за звітний період до його середньорічного значення Кс=Yn/  . Сукупність коефіцієнтів сезонності утворюють сезонну хвилю. Її використовують для визначення загальної тенденції сезонності. Середньорічний коефіцієнт сезонності – відношення середнього лінійного відхилення до середнього значення показника
. Сукупність коефіцієнтів сезонності утворюють сезонну хвилю. Її використовують для визначення загальної тенденції сезонності. Середньорічний коефіцієнт сезонності – відношення середнього лінійного відхилення до середнього значення показника 
62.Прийоми аналізу рядів динаміки.
1. прийоми виявлення загальної тенденції: згладжування шляхом укрупнення інтервалів – визначення середніх значень показників для збільшення періодів часу, кожен такий інтервал включає декілька періодів. Згладжування способом ковзної середньої – первинні рівні ряду динаміки замінюють середніми по збільшених інтервалах, кожний наступний інтервал утворюється з попереднього поступовим зміщення на один період. Аналітичне вирівнювання проводиться за допомогою обраної залежно від характеру динаміки математичної формули, яка відображає загальну тенденцію.
2.прийоми вирівнювання динамічних рядів: змикання ряду динаміки застосовують, коли явища за деякими ознаками є неспівставними. Неспівставність може бути наслідком територіальних знім. В цьому випадку визначають коефіцієнт зімкнення ДР Кз=Ун/Ус. Приведення рівнів ряду динаміки до однієї основи використовують, коли виникає потреба порівняти зміну динамічних рядів кількох споріднених або взаємопов’язаних явищ для цього абсолютні показники перетворюють у відносні, прийнявши ріві будь-якого періоду за 1 або 100%. Інтер-, екстраполяція. інтерполяція – це знаходження невідомого або відсутнього рівня ДР в середині періодів дослідження. Екстраполяція – розрахунок показників, які можуть знаходитися за межами досліджуваного явищаю
63.Загальне поняття індексів.
Індекс – це статистичний відносний показник, що характеризує співвідношення соціально-економічних явищ у часі, просторі або ступінь відхилення показника від певного стандарту, нормативу.
64.Види індексів
1)характер досліджуваних об’єктів: індекси обємних показників фізичного обсягу продукції, товарообороту, витрат на вир-во, фонду оплати праці; індекси якісних показників. 2)ступінь охоплення одиниць сукупності: індивідуальні; загальні. 3) методологія обчислення(тільки для загальних індексів): агрегатні; середні з індивідуальних. 4) база порівняння: базисні; ланцюгові. 5)індекси середніх величин: змінного складу; постійного складу; структурних зрушень.
68.
Арифметичний індекс – одна з форм індексу, яка є середнім арифметичним індивідуальних індексів. Критерій правильності побудови середнього індексу – його рівність агрегатному індексу. Середня арифметична проста з індивідуальних індексів не застосовується, оскільки в ній відображена питома вага кожного окремого елемента в усій сукупності, а застосовують лише як зважений, тотожний агрегатному індексу. Перетворення агрегатного індексу на середній з індивідуальних індексів відбувається підстановкою або в чисельник, або у знаменник агрегатного індексу замість індексного показника його вираження, який виводиться з формули відповідного індивідуального індексу. Така підстановка перетворює в чисельнику агрегатний індекс на середній арифметичний, у знаменнику – на середній гармонійний з індивідуальних індексів.
69.
Відносний показник зміни складного економічного явища, що являє собою середню гармонійну зважену з індивідуальних індексів. Формулу І.г. одержують, замінюючи у знаменнику агрегатного індексу індексовану величину її значенням, вираженим через індивідуальний індекс. І.г. тотожний індексові агрегатному.
70.
Найважливіші економічні індекси та їх взаємозв'язку Між найважливішими індексами існують взаємозв'язки, що дозволяють на основі одних індексів отримувати інші. Знаючи, наприклад, значення ланцюгових індексів за будь-який період часу можна розрахувати базисні індекси. І навпаки, якщо відомі базисні індекси, то шляхом поділу одного з них на інший можна отримати ланцюгові індекси.
Існуючі взаємозв'язки між найважливішими індексами дозволяють виявити вплив різних чинників на зміну досліджуваного явища, наприклад зв'язок між індексом вартості продукції, фізичного обсягу продукції і цін. Інші індекси також пов'язані між собою. Так,. Індекс витрат часу на виробництво продукції може бути отриманий в результаті множення індексу фізичного обсягу продукції і величини, зворотної величиною індексу трудомісткості, тобто індекс продуктивності праці:
. Існує важлива взаємозв'язок між індексами фізичного обсягу продукції та індексом продуктивності праці.
Взаємозв'язок між окремими індексами може бути використана для виявлення окремих факторів, що впливають на досліджуване явище.
71.
Індивідуальні індекси визначаються по окремих одиницях статистичної сукупності та характеризують зміну індивідуальних значень індексованого показника. Ці індекси прийнято позначати і з підстроковим позначенням індексованого показника. Індивідуальні індекси якісних показників визначаються за формулами:
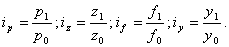
Індивідуальні індекси кількісних показників мають вигляд:

72.
Індекс, який характеризує спільний вплив обох чинників, називається індексом змінного складу і визначається за формулою:

На величину індекса собівартості змінного складу впливають зміни рівнів собівартості і зміни в структурі (її складі). Щоб виявити роль кожного чинника в загальній динаміці середньої, потрібно індекс змінного складу розкласти на два індекси-співмножники, кожний з яких відображає вплив тільки одного чинника.
Перший індекс, який характеризує вплив тільки індексованої величини (в якому змінюється лише собівартість), називається індексом постійного (фіксованого) складу. Він обчислюється за формулою:

73.
Залежно від того, що приймається за базу порівняння, індекси бувають базисні та ланцюгові.
Базисні індекси одержують шляхом порівняння абсолютних рівнів кожного періоду з рівнем якогось періоду (звичайно початкового), прийнятого за базу порівняння.
Ланцюгові індекси одержують шляхом порівняння абсолютного рівня кожного періоду з рівнем попереднього періоду.
75.
Поряд з таблицями для характеристики результатів статистичного зведення і обробки масових даних широко застосовують статистичні графіки.
Статистичним графіком називають наочне масштабне зображення статистичних даних за допомогою геометричних ліній, точок, знаків, фігур, географічних картосхем та інших графічних засобів.
Графічний метод настільки міцно ввійшов в арсенал засобів наукового узагальнення і в методику наукових досліджень, що сучасну науку неможливо собі уявити без його застосування.
74.
При вивченні динаміки діяльності підприємств і організацій виникає необхідність визначити індекси більше, ніж за два періоди. У таких випадках індекси можна розраховувати як на постійній, так і на змінній базах порівняння.
Загальні індекси залежно від їхнього вигляду обчислюють зі змінними та постійними вагами. Якщо сумірники (ваги) в обчислених індексах належать до одного періоду, то це — індекси з постійними вагами і змінними, якщо вони змінюються від індексу до індексу. Так, розглянуту вище агрегатну форму загального індексу фізичного обсягу обчислювали як індекс за постійними вагами-сумірниками. Агрегатну форму загального індексу цін розраховують як індекс зі змінними вагами-сумірниками.
76. Застосування графічного методу у вивченні масових соціально - економічних явищ досить різнопланове. Так, графіки застосовують для характеристики змін суспільних явищ і процесів у часі, вивчення структури явищ, порівняння, контролю виконання плану, дослідження взаємозв'язків між результативними і факторними ознаками, зображення розміщення явищ у просторі, ступеня розповсюдженості по території тих чи інших явищ, міжнародних порівнянь і зіставлень та в інших випадках.
Особливо велика роль графіків у пропаганді передового досвіду, прогресивних тенденцій, закономірностей, нових технологій, наукових досягнень та ін.
77.
Статистичні графіки за напрямом використання характеризуються значною різноманітністю. їх наукова класифікація передбачає такі ознаки, як загальне призначення, види, форми і типи основних елементів. Традиційно теорія статистики розглядає класифікацію графіків за видами їх поля. За цим принципом графічні зображення поділяють на діаграми, картограми та картодіаграми.
Діаграми -це умовні зображення числових величин та їх співвідношень за допомогою геометричних знаків.
Картограми - зображення числових величин та їх співвідношень за допомогою нанесення умовної штриховки або розцвітки на карту - схему.
Картодіаграми -це поєднання діаграми із картою - схемою. При побудові діаграми встановлюється певний масштаб, тобто співвідношення між розмірами величин на графіку і дійсною величиною зображуваного явища в натурі.
78.
Графічна мова вважається специфічною формою наукового мислення та узагальнення. Це особлива форма інформації, яка трактується в сучасних поняттях теорії пізнання як своєрідна знакова система.
Мова статистичних графіків належить до умовних символічних мов і має такі особливості:
1) двомірність графічних знаків, тобто домірність запису.
2) безперервність виразу. У статистичних графіках відповідна інформація представлена не окремими дискретними знаками, а взаємопов'язаною системою, геометрично орієнтованою у просторі. 3) відокремленість викладу. Статистичні графіки як знаряддя наукової інформації відособлюються від тексту взаємопов'язаної за змістом інформації, яка подається в усній або письмовій формі. Тимчасом як мова математики (фізики чи хімії), як правило пов'язана з такими формами подання інформації.
79.
Статистичний графік являє собою рисунок, який описує статистичні сукупності умовною мовою геометричних знаків тієї чи іншої форми крапок, ліній, площин, фігур та різних їх комбінацій.
складові елементи. Поле графіка - це простір, в якому розміщуються геометричні або інші графічні знаки, що утворюють графік. Розмір поля графіка залежить від його призначення і характеризується розміром та пропорціями сторін
Геометричні знаки (або графічні образи) - сукупність геометричних або графічних знаків для зображення статистичних даних. Насамперед це крапки, за допомогою яких наочно зображуються лічильні множини, тобто окремі елементи статистичної сукупності..
Значне місце в цій системі займають знаки у вигляді площин різних геометричних форм (квадрат, сектор, коло і т.п.). їх використовують для порівняння явищ, які характеризуються абсолютними і відносними величинами.
80.
Найбільш поширеним видом статистичних графіків є діаграми. Залежно від способу зображення статистичних даних вони можуть бути в одному виміру, коли ці дані зображують у вигляді прямих ліній або смуг однакової ширини, і в двох вимірах (площині), на яких даних зображують за допомогою площ геометричних фігур (прямокутників, квадратів, кіл.).
До першого виду діаграм належать лінійні, стовпчикові, стрічкові та ін.; до другого - прямокутні (квадратні, "Знак Варвара"), колові, секторні, радіальні, фігурні.
Лінійна діаграма відображує розмір показника у формі ліній різної довжини, які утворюються в результаті з'єднання крапок у координатному полі. Одним із видів лінійних діаграм є лінійний графік виконання плану та обліково-плановий графік
81.
Графіки, які ілюструють зміну статистичних явищ в часі називаються динамічними. Для зображення динаміки явищ часто використовують розглянуті нами в п. 5.2 стовпчикові, стрічкові, квадратні, кругові і картинні діаграми, в яких кожний стовпчик, стрічка, квадрат і т.д. зображають величину статистичного явища на певну дату, або за відповідний проміжок часу.
Крім названих вище графіків нерідко застосовуються і лінійні графіки.
Лінійні графіки використовуються для характеристики зміни явищ в часі, виявлення залежності між двома показниками і деяких інших завдань. Вони будуються при допомозі прямокутної системи
координат, на осі абсцис якої розміщують шкалу характеристик часу, a на осі ординат - рівні ряду динаміки.
У лінійній діаграмі динаміки шкала на осі ординат повинна починатися з нуля, інакше діаграма буде не правильно відображати характер розвитку явища.
82.
Діаграми - це умовне зображення числових величин та їх співвідношень за допомогою геометричних знаків. Термін "діаграма" тотожний терміну "статистичний графік". Діаграми є найбільш розповсюдженим видом графіків. Виділяють такі основні види діаграм: лінійні, стовпчикові, стрічкові, квадратні, секторні, радіальні, трикутні, фігурні, знак Варзара та ін.
Залежно від кола розв'язуваних завдань усі діаграми можна поділити на діаграми порівняння, структури та динаміки.
Розглянемо методику і техніку побудови статистичних графіків, що найчастіше застосовуються на практиці.
Найрозповсюдженішим видом показових діаграм є лінійні діаграми, які використовуються здебільшого для характеристики динамічних рядів та рядів розподілу. Поряд з цим лінійні діаграми широко використовуються для вивчення взаємозв'язків між явищами, порівняння кількох показників, ходу виконання планів тощо.
Лінійні діаграми дають можливість зображати явища у вигляді ліній, які з'єднують точки, розташовані у координатному полі. Ламані лінії, що утворюються, показують характер розвитку явища у часі або особливості його розподілу за величиною якої-небудь ознаки, або зв'язку явищ.
83.
Для кращого сприйняття й зрозуміння закономірностей явищ і процесів у економічному аналізі широко застосовуються графічні способи зображення інформації.
Наявність потужних і зручних програм для аналізу статистичних даних на персональних комп’ютерах, і зокрема, формування електронних таблиць Microsoft Excel для Windows розширює коло споживачів методів графічного зображення статистичної інформації, що визначає актуальність дослідження.
Мета статті – розкрити основні елементи графічного методу.
Статистичний графік являє собою систему подання інформації про соціально-економічні явища за допомогою наочного зображення статистичних числовий величин та їх співвідношень з використанням знакових систем: крапок; знаків ліній; геометричних фігур, малюнків з метою їх узагальнення й подальшого аналізу [2, с. 68]. Графіки мають ту перевагу перед текстовим викладом і статистичними таблицями, що дають наочні результати статистичного зведення і обробки основного матеріалу. За допомогою графіків легко виявити і наочно подати закономірності, які важко вловити в складних статистичних таблицях.
84.
Графічний метод широко використовується для поточного контролю за ходом виконання плану. Форми графічного зображення для порівняння планових і фактичних показників досить різноманітні. В даному розділі розглянемо два основних види графіків:
а) лінійні графіки виконання плану;
б) обліково-планові графіки.
Лінійні графіки є зручними засобом контролю виконання плану по одному якому-небудь об'єкту або показнику. При цьому для аналізу на графіку доцільно показати наростаючим підсумком не тільки планові і фактичні показники у звітному періоді, але й фактичні - за минулий рік.
В тих випадках, коли потрібно організувати наочний контроль виконання плану одночасно на декількох об’єктах, будують обліково-планові графіки.
їх будують на спеціально розграфленій сітці, яка має форму таблиці, і на якій по горизонталі відкладають одиниці часу (день, п'ятиденку, декаду, місяць, квартал), a no вертикалі розміщують об'єкти дослідження.
85.
По способі побудови статистичні графіки поділяються на діаграми і статистичні карти.
Діаграми - найбільш розповсюджений спосіб графічних зображень. Це графіки кількісних відносин. Види і способи їхньої побудови різноманітні. Діаграми застосовуються для наочного зіставлення в різних аспектах (просторовому, тимчасовому й ін.) незалежних друг від друга величин:
територій, населення і т.д.
При цьому порівняння досліджуваних сукупностей виробляється по якій-небудь істотній ознаці, що варіює, Статистичнікарти - графіки кількісного розподілу по поверхні. По своїй основній меті вони близько примикають до діаграм і специфічні лише в тім відношенні, що являють собою умовні зображення статистичних даних на контурній географічній карті, тобто показують просторове чи розміщення просторову поширеність статистичних даних. Геометричні знаки як було сказано вище, - це або крапки, або чи лінії площини, або геометричні тіла. Відповідно до цього розрізняють графіки крапкові, лінійні, площинні і просторові (об'ємні).
68.
Арифметичний індекс – одна з форм індексу, яка є середнім арифметичним індивідуальних індексів. Критерій правильності побудови середнього індексу – його рівність агрегатному індексу. Середня арифметична проста з індивідуальних індексів не застосовується, оскільки в ній відображена питома вага кожного окремого елемента в усій сукупності, а застосовують лише як зважений, тотожний агрегатному індексу. Перетворення агрегатного індексу на середній з індивідуальних індексів відбувається підстановкою або в чисельник, або у знаменник агрегатного індексу замість індексного показника його вираження, який виводиться з формули відповідного індивідуального індексу. Така підстановка перетворює в чисельнику агрегатний індекс на середній арифметичний, у знаменнику – на середній гармонійний з індивідуальних індексів.
69.
Відносний показник зміни складного економічного явища, що являє собою середню гармонійну зважену з індивідуальних індексів. Формулу І.г. одержують, замінюючи у знаменнику агрегатного індексу індексовану величину її значенням, вираженим через індивідуальний індекс. І.г. тотожний індексові агрегатному.
70.
Найважливіші економічні індекси та їх взаємозв'язку Між найважливішими індексами існують взаємозв'язки, що дозволяють на основі одних індексів отримувати інші. Знаючи, наприклад, значення ланцюгових індексів за будь-який період часу можна розрахувати базисні індекси. І навпаки, якщо відомі базисні індекси, то шляхом поділу одного з них на інший можна отримати ланцюгові індекси.
Існуючі взаємозв'язки між найважливішими індексами дозволяють виявити вплив різних чинників на зміну досліджуваного явища, наприклад зв'язок між індексом вартості продукції, фізичного обсягу продукції і цін. Інші індекси також пов'язані між собою. Так,. Індекс витрат часу на виробництво продукції може бути отриманий в результаті множення індексу фізичного обсягу продукції і величини, зворотної величиною індексу трудомісткості, тобто індекс продуктивності праці:
. Існує важлива взаємозв'язок між індексами фізичного обсягу продукції та індексом продуктивності праці.
Взаємозв'язок між окремими індексами може бути використана для виявлення окремих факторів, що впливають на досліджуване явище.
71.
Індивідуальні індекси визначаються по окремих одиницях статистичної сукупності та характеризують зміну індивідуальних значень індексованого показника. Ці індекси прийнято позначати і з підстроковим позначенням індексованого показника. Індивідуальні індекси якісних показників визначаються за формулами:
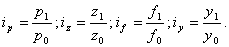
Індивідуальні індекси кількісних показників мають вигляд:

72.
Індекс, який характеризує спільний вплив обох чинників, називається індексом змінного складу і визначається за формулою:

На величину індекса собівартості змінного складу впливають зміни рівнів собівартості і зміни в структурі (її складі). Щоб виявити роль кожного чинника в загальній динаміці середньої, потрібно індекс змінного складу розкласти на два індекси-співмножники, кожний з яких відображає вплив тільки одного чинника.
Перший індекс, який характеризує вплив тільки індексованої величини (в якому змінюється лише собівартість), називається індексом постійного (фіксованого) складу. Він обчислюється за формулою:

73.
Залежно від того, що приймається за базу порівняння, індекси бувають базисні та ланцюгові.
Базисні індекси одержують шляхом порівняння абсолютних рівнів кожного періоду з рівнем якогось періоду (звичайно початкового), прийнятого за базу порівняння.
Ланцюгові індекси одержують шляхом порівняння абсолютного рівня кожного періоду з рівнем попереднього періоду.
75.
Поряд з таблицями для характеристики результатів статистичного зведення і обробки масових даних широко застосовують статистичні графіки.
Статистичним графіком називають наочне масштабне зображення статистичних даних за допомогою геометричних ліній, точок, знаків, фігур, географічних картосхем та інших графічних засобів.
Графічний метод настільки міцно ввійшов в арсенал засобів наукового узагальнення і в методику наукових досліджень, що сучасну науку неможливо собі уявити без його застосування.
74.
При вивченні динаміки діяльності підприємств і організацій виникає необхідність визначити індекси більше, ніж за два періоди. У таких випадках індекси можна розраховувати як на постійній, так і на змінній базах порівняння.
Загальні індекси залежно від їхнього вигляду обчислюють зі змінними та постійними вагами. Якщо сумірники (ваги) в обчислених індексах належать до одного періоду, то це — індекси з постійними вагами і змінними, якщо вони змінюються від індексу до індексу. Так, розглянуту вище агрегатну форму загального індексу фізичного обсягу обчислювали як індекс за постійними вагами-сумірниками. Агрегатну форму загального індексу цін розраховують як індекс зі змінними вагами-сумірниками.
76. Застосування графічного методу у вивченні масових соціально - економічних явищ досить різнопланове. Так, графіки застосовують для характеристики змін суспільних явищ і процесів у часі, вивчення структури явищ, порівняння, контролю виконання плану, дослідження взаємозв'язків між результативними і факторними ознаками, зображення розміщення явищ у просторі, ступеня розповсюдженості по території тих чи інших явищ, міжнародних порівнянь і зіставлень та в інших випадках.
Особливо велика роль графіків у пропаганді передового досвіду, прогресивних тенденцій, закономірностей, нових технологій, наукових досягнень та ін.
77.
Статистичні графіки за напрямом використання характеризуються значною різноманітністю. їх наукова класифікація передбачає такі ознаки, як загальне призначення, види, форми і типи основних елементів. Традиційно теорія статистики розглядає класифікацію графіків за видами їх поля. За цим принципом графічні зображення поділяють на діаграми, картограми та картодіаграми.
Діаграми -це умовні зображення числових величин та їх співвідношень за допомогою геометричних знаків.
Картограми - зображення числових величин та їх співвідношень за допомогою нанесення умовної штриховки або розцвітки на карту - схему.
Картодіаграми -це поєднання діаграми із картою - схемою. При побудові діаграми встановлюється певний масштаб, тобто співвідношення між розмірами величин на графіку і дійсною величиною зображуваного явища в натурі.
78.
Графічна мова вважається специфічною формою наукового мислення та узагальнення. Це особлива форма інформації, яка трактується в сучасних поняттях теорії пізнання як своєрідна знакова система.
Мова статистичних графіків належить до умовних символічних мов і має такі особливості:
1) двомірність графічних знаків, тобто домірність запису.
2) безперервність виразу. У статистичних графіках відповідна інформація представлена не окремими дискретними знаками, а взаємопов'язаною системою, геометрично орієнтованою у просторі. 3) відокремленість викладу. Статистичні графіки як знаряддя наукової інформації відособлюються від тексту взаємопов'язаної за змістом інформації, яка подається в усній або письмовій формі. Тимчасом як мова математики (фізики чи хімії), як правило пов'язана з такими формами подання інформації.
79.
Статистичний графік являє собою рисунок, який описує статистичні сукупності умовною мовою геометричних знаків тієї чи іншої форми крапок, ліній, площин, фігур та різних їх комбінацій.
складові елементи. Поле графіка - це простір, в якому розміщуються геометричні або інші графічні знаки, що утворюють графік. Розмір поля графіка залежить від його призначення і характеризується розміром та пропорціями сторін
Геометричні знаки (або графічні образи) - сукупність геометричних або графічних знаків для зображення статистичних даних. Насамперед це крапки, за допомогою яких наочно зображуються лічильні множини, тобто окремі елементи статистичної сукупності..
Значне місце в цій системі займають знаки у вигляді площин різних геометричних форм (квадрат, сектор, коло і т.п.). їх використовують для порівняння явищ, які характеризуються абсолютними і відносними величинами.
80.
Найбільш поширеним видом статистичних графіків є діаграми. Залежно від способу зображення статистичних даних вони можуть бути в одному виміру, коли ці дані зображують у вигляді прямих ліній або смуг однакової ширини, і в двох вимірах (площині), на яких даних зображують за допомогою площ геометричних фігур (прямокутників, квадратів, кіл.).
До першого виду діаграм належать лінійні, стовпчикові, стрічкові та ін.; до другого - прямокутні (квадратні, "Знак Варвара"), колові, секторні, радіальні, фігурні.
Лінійна діаграма відображує розмір показника у формі ліній різної довжини, які утворюються в результаті з'єднання крапок у координатному полі. Одним із видів лінійних діаграм є лінійний графік виконання плану та обліково-плановий графік
81.
Графіки, які ілюструють зміну статистичних явищ в часі називаються динамічними. Для зображення динаміки явищ часто використовують розглянуті нами в п. 5.2 стовпчикові, стрічкові, квадратні, кругові і картинні діаграми, в яких кожний стовпчик, стрічка, квадрат і т.д. зображають величину статистичного явища на певну дату, або за відповідний проміжок часу.
Крім названих вище графіків нерідко застосовуються і лінійні графіки.
Лінійні графіки використовуються для характеристики зміни явищ в часі, виявлення залежності між двома показниками і деяких інших завдань. Вони будуються при допомозі прямокутної системи
координат, на осі абсцис якої розміщують шкалу характеристик часу, a на осі ординат - рівні ряду динаміки.
У лінійній діаграмі динаміки шкала на осі ординат повинна починатися з нуля, інакше діаграма буде не правильно відображати характер розвитку явища.
82.
Діаграми - це умовне зображення числових величин та їх співвідношень за допомогою геометричних знаків. Термін "діаграма" тотожний терміну "статистичний графік". Діаграми є найбільш розповсюдженим видом графіків. Виділяють такі основні види діаграм: лінійні, стовпчикові, стрічкові, квадратні, секторні, радіальні, трикутні, фігурні, знак Варзара та ін.
Залежно від кола розв'язуваних завдань усі діаграми можна поділити на діаграми порівняння, структури та динаміки.
Розглянемо методику і техніку побудови статистичних графіків, що найчастіше застосовуються на практиці.
Найрозповсюдженішим видом показових діаграм є лінійні діаграми, які використовуються здебільшого для характеристики динамічних рядів та рядів розподілу. Поряд з цим лінійні діаграми широко використовуються для вивчення взаємозв'язків між явищами, порівняння кількох показників, ходу виконання планів тощо.
Лінійні діаграми дають можливість зображати явища у вигляді ліній, які з'єднують точки, розташовані у координатному полі. Ламані лінії, що утворюються, показують характер розвитку явища у часі або особливості його розподілу за величиною якої-небудь ознаки, або зв'язку явищ.
83.
Для кращого сприйняття й зрозуміння закономірностей явищ і процесів у економічному аналізі широко застосовуються графічні способи зображення інформації.
Наявність потужних і зручних програм для аналізу статистичних даних на персональних комп’ютерах, і зокрема, формування електронних таблиць Microsoft Excel для Windows розширює коло споживачів методів графічного зображення статистичної інформації, що визначає актуальність дослідження.
Мета статті – розкрити основні елементи графічного методу.
Статистичний графік являє собою систему подання інформації про соціально-економічні явища за допомогою наочного зображення статистичних числовий величин та їх співвідношень з використанням знакових систем: крапок; знаків ліній; геометричних фігур, малюнків з метою їх узагальнення й подальшого аналізу [2, с. 68]. Графіки мають ту перевагу перед текстовим викладом і статистичними таблицями, що дають наочні результати статистичного зведення і обробки основного матеріалу. За допомогою графіків легко виявити і наочно подати закономірності, які важко вловити в складних статистичних таблицях.
84.
Графічний метод широко використовується для поточного контролю за ходом виконання плану. Форми графічного зображення для порівняння планових і фактичних показників досить різноманітні. В даному розділі розглянемо два основних види графіків:
а) лінійні графіки виконання плану;
б) обліково-планові графіки.
Лінійні графіки є зручними засобом контролю виконання плану по одному якому-небудь об'єкту або показнику. При цьому для аналізу на графіку доцільно показати наростаючим підсумком не тільки планові і фактичні показники у звітному періоді, але й фактичні - за минулий рік.
В тих випадках, коли потрібно організувати наочний контроль виконання плану одночасно на декількох об’єктах, будують обліково-планові графіки.
їх будують на спеціально розграфленій сітці, яка має форму таблиці, і на якій по горизонталі відкладають одиниці часу (день, п'ятиденку, декаду, місяць, квартал), a no вертикалі розміщують об'єкти дослідження.
85.
По способі побудови статистичні графіки поділяються на діаграми і статистичні карти.
Діаграми - найбільш розповсюджений спосіб графічних зображень. Це графіки кількісних відносин. Види і способи їхньої побудови різноманітні. Діаграми застосовуються для наочного зіставлення в різних аспектах (просторовому, тимчасовому й ін.) незалежних друг від друга величин:
територій, населення і т.д.
При цьому порівняння досліджуваних сукупностей виробляється по якій-небудь істотній ознаці, що варіює, Статистичнікарти - графіки кількісного розподілу по поверхні. По своїй основній меті вони близько примикають до діаграм і специфічні лише в тім відношенні, що являють собою умовні зображення статистичних даних на контурній географічній карті, тобто показують просторове чи розміщення просторову поширеність статистичних даних. Геометричні знаки як було сказано вище, - це або крапки, або чи лінії площини, або геометричні тіла. Відповідно до цього розрізняють графіки крапкові, лінійні, площинні і просторові (об'ємні).
Не нашли, что искали? Воспользуйтесь поиском: