
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Ателіктердің протуберанциясы деген ұғымға түсініктеме беріңіз. Гистограммалардың құрылуы және оны сипаттаңыз.
1). Вариациялық қатарды гистограмма сызу арқылы көрсету.
Кластарға жіктелген вариациялық қатарды график арқылы бейнелеу гистограмма деп атадалады. Гистограмма жасаған кезде горизонталь осьтің бойына кластардың мөлшерін, ал вертикаль осьтің бойына жиіліктерді орналластырады. Гистограмманы вариациялық қисыққа айналдыруға болады. Ол үшін кластардың ортасын түзу сызықтармен қосу керек.
Белгілерді талдау кезінде әдетте зерттеуші көп санды мәліметтерді алады Гистограммалар мен вариациялық қисықтар құру сол алынған көп санды мәліметтердің мәнін түсінуге жәңе олардан қандай да болмасын белгілі заңдылық табуға көмектеседі. Салыстыруға ыңғайлы болу үшін бір чертежде кейбірде бірнеше қисықтар беріледі. Ол қисықтарды бір-бірінен ажырату үшін оларды әртүрлі түспен немесе әртүрлі штрифтармен көрсетеді, яғни әр вариаттың өзінің экспликациясы болады.
Биологиялық объектілердің көптеген белгілеріне қалыпты таралу тән. Оның бір ерекшелігі, жекеленген варианттың маңызы орташа шамадан ауытқыған сайын оның көрінуі төмендейді. Мысалы орташа бойлы адамдар жиі кездеседі, ал алыптылар мен ергежейлілер өте сирек кездеседі.
2) Таралу полигоны.
Кез-келгкен вариациялық қатардың графикалық көрінісінен биномиалды қисықтың (полигон) таралуы деп аталатын параболаны аламыз. Сонымен варианттың таралуы сол немесе басқа варианттың кездесу ықтималдығының кішіреюі теориялық заңдылыққа негізделген
Мысалы 2 тиынды біруақытта жоғары лақтырамыз. Герб жағымен (Г) жоғары қарап түсуі – бұл қолайлы жағдай дейік, ал торлар жағымен түсуі (Т) – қолайсыз жағдай. Бірінші жағдайда екі тиын да герб жағымен жоғары ГГ қарап түседі, екінші жағдайда бірінші тиын герб жағымен жоғары екінші тиын тор жағымен ГТ, үшінші жағдайда бірінші тиын Т, екінші тиын Г, яғни ТГ, төртінші жағдайда екі тиын да тор болып түседі – ТТ. Герб жағымен жоғары қарап түсу ықтималдығын p2, - төмен – g2, ал біруақытта бір тиынның герб жағымен жоғары қарап, екінші тиынның төмен қарап түсу ықтималдығы - 2pg. Оны мына формулаға саламыз: (p + g)2 = p 2 +2 p g + g2, бұл Ньютонның биномның таралуы деген формуласына сәйкес келеді.
Барлық жағдайда тәуелсіз әртүрлі қосылыстардың ықтималдықтарының алынуы мынаған негізделген, яғни бірнеше комбинацияның ықтималдығы биномның таралу мүшелерімен анықталады (p + g) k, мұндағы k – тәуелсіз кездейсоқ жағдайлардың саны, ал p және g қолайлы және қолайсыз жағдайларының ықтималдығына сәйкес келеді. (p + g) k формуласында k-ның шексіздікке жақындауынан таралу үздіксіз бола бастайды, ал таралу полигоны симметриялық ирек қисыққа айналады. Бұл қалыпты вариациялық қисық деген атқа ие болды, ал таралудың өзі қалыпты деп аталады. Қазіргі кезде қалыпты таралу жағдайында вариацияның заңдылықтарын зерттеу үшін дұрыс ауытқуды кең қолданады, ол t әрпімен белгіленеді. Дұрыс ауытқу бұл сигмамен көрсетілген сол немесе басқа варианттың арифметикалық орташасынан ауытқуын айтамыз. Сол немесе басқа белгі бойынша варианттың таралуы айтамыз.
xi - х
t = -------------, мұндағы xi -`х = t Q
Q
Сол немесе басқа белгі бойынша вариант таралуының вариациялық қисығын біле отырып және таралуы қалыпты екенін болжай отырып зерттелген даралардың (вариант) қанша үлесі шегіне жетеді екендігін анықтауға болады +\- 1 Q, +\- 2 Q, +\- 3 Q. Мысалы, +\- 1 Q шегінде барлық даралардың 68,3 % таралады, +\- 2 Q – 95 шегінде 5 %, ал +\- 3 Q – 99,7 % таралады.
4.Арифметикалық орта шама және оның қасиеті. Түзетбе, орташа шама, ауытқу түсініктеріне анықтама беріңіз.
Материалды статистикалық өңдеудің негізгі мақсаттарының бірі- тәжірибеден алынған жиынтықтардың өздеріне тән ерекшеліктерін сипаттайтын көрсеткіштерін табу және оларды бір-бірімен салыстыру болып табылады.
Статистикалық жиынтықтарды екі көрсеткіш жеткілікті, толық сипаттай алады:
1. Белгінің орташа мөлшері
2. Өзгергіштік немесе шашырап бытырау (рассеяния) дәрежесі
“Белгілердің орташа мөлшері” ұғымын қарастырайық. Статистикада арифметикалық орта шама, өлшелінген орта шама, геометриялық орта шама, гармониялық орташама ұғымдары қолданылады. Биологиялық және ауылшаруашылық ғылыми-зерттеу жұмыстарында көбінесе арифметикалық орта шаманы табудың үлкен маңызы бар.
Өзінен оң және теріс ауытқуларының қосындысы нөлге тең шама – арифметикалық орта шама деп аталады. Арифметикалық орта шаманы табу үшін барлық варианттарды қосады және оларды бақылаулар санына бөледі.
Вариациялық статистикада арифметикалық орта шама М немесе ‾х (икс покрытое деп оқылады) арқылы белгіленеді.
Орта арифметикалық шаманың қасиеттері:
1) ол ортада болуы керек
2) абстракты өлшем 
3) жиынтық әсерінің бірлігі – орта арифметикалық шаманы бақылау санынна көбейтеді:
∑х = хn
5.Қандай жағдайда арифметикалық орташа шаманы есептеуде “моменттер тәсілін” қолдану керектігін түсіндіріңіз.
Варианттар саны көп болған жағдайда орта арифметикалық шаманы табу қиындау, сондықтан, оны оңай жолмен - «моменттер тәсілін» қолдана отырып табуға болады. Ол үшін варияциалық қатардың дәл ортасында немесе ортасында жатқан вариантты шектеп алып оны шартты орта шама деп белгілейміз. Шартты орта шаманы хо символымен белгілейді. Арифметикалық орта шаманы табу үшін шартты орта шаманың түзетпесін табу керек. Түзетпе b символымен белгіленеді және оны табу үшін оң және теріс ауытқулардың қосындысын бақылау санына (n) бөледі, кестеде көрсетілгендей:: 
Кластарға жіктелген вариациялық қатарлардан орта шама тапқан кезде әр кластың кездейсоқ алынған шартты орта кластан ауытқуы бірге тең деп есептелінеді. Сонан соң табылған түзетуді k немесе l әріптерімен белгіленетін класс мөлшеріне көбейтеді де, таңбасына қарай кездейсоқ шартты орта кластың шамасына не қосады, не одан алып тастайды. Кездейсоқ кластың орталық мәні W немесе х арқылы белгіленеді.
Соңыңда орта арифметикалық шаманы мына формуламен табады 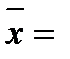 xo +(± b), кластарға жіктелген вариациялық қатарларда l көрсеткішке көбейтеді
xo +(± b), кластарға жіктелген вариациялық қатарларда l көрсеткішке көбейтеді 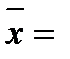 xo +(± b) х l
xo +(± b) х l
6.Класқа бөлінген варианттардың арифметикалық орта шамасын қандай жолмен табатындығына көрсетіңіз.
Өзінен оң және теріс ауытқуларының қосындысы нөлге тең шама – арифметикалық орта шама деп аталады. Арифметикалық орта шаманы табу үшін барлық варианттарды қосады және оларды бақылаулар санына бөледі.
Вариациялық статистикада арифметикалық орта шама М немесе ‾х (икс покрытое деп оқылады) арқылы белгіленеді.
Орта арифметикалық шаманың қасиеттері:
1) ол ортада болуы керек
2) абстракты өлшем 
3) жиынтық әсерінің бірлігі – орта арифметикалық шаманы бақылау санынна көбейтеді:
∑х = хn
7.Вариация коэффициентін анықтайтын формуланы көрсетіңіз. Сигма, лимиттер деген терминдерді түсіндіріңіз.
Зерттеу үшін алынған әрьір жеке жиынтықтардың жекелеген даналары орта мөлшерден әр дәрежеде ауытқиды, сондықтан зерттелуге тиісті іріктеуді сипаттау үшін тек арифметикалық орта шаманы табу жеткіліксіз. Мұндайда осы әртүрлілік дәрежесін сипаттай алатындай көрсеткіштер келтіру керек.
Белгілер әртүрлілігінің көрсеткіштері қызметін лимиттер өзгергіштіктің шайқалу шегі, орташа квадраттық ауытқу δ (сигма), варианса δ2 және вариация коэффициенті С.v. атқарады. Әртүрлілік көрсеткіштерінің бәріне тән жалпы қасиет олар осы санаулан әртүрлілік ерекшеліктерінің қандай дәрежесі болса да нақты белгілей алады.
Зерттелетін жиынтықты сиппаттау үшін орта шаманы ғана анықтап қою жеткіліксіз, әртүрліліктің дәрежесін сиппаттайтын көрсеткішті келтіру қажет. Белгілі математик Гаусс әртүрлілік дәрежесінің көрсеткіші ретінде негізгі ауытқуды пайдалану керектігін ұсынды. Өзгергіштіктің әртүрлілігінің дәрежесін орташаквадраттық ауытқунемесе негізгі ауытқукөрсетеді, оны  символымен белгілейді. Гаусс ұсынған негізгі ауытқудың формуласы
символымен белгілейді. Гаусс ұсынған негізгі ауытқудың формуласы
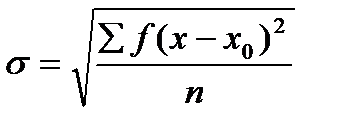
Оң және теріс ауытқулардың қосындысы х -ге тең болатыны белгілі. Сондықтан ауытқуларды дәрежелегенде (квадраттағанда) барлық таңбалар оң, демек олардың қосындылары да оң шама болып шығады. Кейбір жекелеген жиынтықтар шамаларының әсерін жоғалту үшін ауытқулар квадраттарымен жиіліктер көбейтінділерінің қосындысын бақылаулар санына бөледі.
Кейіннен Гаустың бұл формуласы аздап өзгерді:

Бұл формула күрделі вариациялық қатарға қолданылады. Формуланы оқитын болсақ, негізгі ауытқу тең болады - ауытқулар квадратының жиілікке көбейтіндісінің жалпы санын ерікті дәрежелерге бөліп, одан түзетпенің квадратын алып тастап, түбір астынан шыққан санды кластар көлеміне көбейту керек.
8.Орташа квадраттық ауытқу деген ұғымға түсініктеме беріңіз.
Зерттеу үшін алынған әрьір жеке жиынтықтардың жекелеген даналары орта мөлшерден әр дәрежеде ауытқиды, сондықтан зерттелуге тиісті іріктеуді сипаттау үшін тек арифметикалық орта шаманы табу жеткіліксіз. Мұндайда осы әртүрлілік дәрежесін сипаттай алатындай көрсеткіштер келтіру керек.
Белгілер әртүрлілігінің көрсеткіштері қызметін лимиттер өзгергіштіктің шайқалу шегі, орташа квадраттық ауытқу δ (сигма), варианса δ2 және вариация коэффициенті С.v. атқарады. Әртүрлілік көрсеткіштерінің бәріне тән жалпы қасиет олар осы санаулан әртүрлілік ерекшеліктерінің қандай дәрежесі болса да нақты белгілей алады.
Зерттелетін жиынтықты сиппаттау үшін орта шаманы ғана анықтап қою жеткіліксіз, әртүрліліктің дәрежесін сиппаттайтын көрсеткішті келтіру қажет. Белгілі математик Гаусс әртүрлілік дәрежесінің көрсеткіші ретінде негізгі ауытқуды пайдалану керектігін ұсынды. Өзгергіштіктің әртүрлілігінің дәрежесін орташаквадраттық ауытқунемесе негізгі ауытқукөрсетеді, оны  символымен белгілейді. Гаусс ұсынған негізгі ауытқудың формуласы
символымен белгілейді. Гаусс ұсынған негізгі ауытқудың формуласы
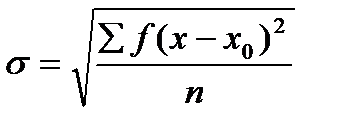
Оң және теріс ауытқулардың қосындысы х -ге тең болатыны белгілі. Сондықтан ауытқуларды дәрежелегенде (квадраттағанда) барлық таңбалар оң, демек олардың қосындылары да оң шама болып шығады. Кейбір жекелеген жиынтықтар шамаларының әсерін жоғалту үшін ауытқулар квадраттарымен жиіліктер көбейтінділерінің қосындысын бақылаулар санына бөледі.
Кейіннен Гаустың бұл формуласы аздап өзгерді:

Бұл формула күрделі вариациялық қатарға қолданылады. Формуланы оқитын болсақ, негізгі ауытқу тең болады - ауытқулар квадратының жиілікке көбейтіндісінің жалпы санын ерікті дәрежелерге бөліп, одан түзетпенің квадратын алып тастап, түбір астынан шыққан санды кластар көлеміне көбейту керек.
9.Үзілмелі және үзіліссіз сандардан тұратын варианттрады класқа бөліңіз.
Үзілмелі немесе үзіліссіз өзгергіштіктерді зерттеуден алынған мәліметтерді талдау кезінде, егер өзгергіштіктің шайқалу шегі үлкен болса варианттарды кластарға жіктеу керек. Мысалы, бір түрге жататын балықтардың уылдырықтарының саны олардың жас ерекшеліктеріне қарай бір-бірінен 500-ден аса данаға дейін айырмашылық беруі мүмкін. Бұл варианттардың барлығын бір бағана етіп жазу мүмкін емес.
Үзіліссіз өзгергіштіктерге варианттар көп жағдайда аралас сандар брлып келеді, мысалы өсімдіктің биіктігі: 1,25; 2,15; 3,45; м т.б.
Осы сияқты жағдайларда варианттар кластарға жіктеледі, ол үшін мынадай ережелерді ескеру керек:
1. Кластардың шекарасын анықтаған кезде, әр варианта бір ғана класқа кіретін брлуы керек: мысалы 5-9, 10-14, 15-19 т.б. Кластарды ешуақытта 5-10, 10-15, 15-20 деп бөлуге болмайды.
2. Барлық кластардың мөлшері бірдей болуы керек.
3. Бірінші және ақырғы кластар толық болмауы мүмкін. Мысалы, егер кластың мөлшері 10, ал өзгергіштіктің шайқалу шегі 76 болса, 77-79 варианттарының жоқтығына қарамастан ақырғы кластың мөлшері 70-79 болады.
4. Кластардың саны 6-7-ден кем, 10-15-тен артық болмауы керек.
Кластардың мөлшерін анықтау үшін максимум және минимум вариантары табады, одан соң өзгергіштңктің шайқалу шегін анықтайды және оны белгіленген кластардың санына бөледі, алынған санды бүтін санға дейін дөңгелектейді.
Не нашли, что искали? Воспользуйтесь поиском: