Арифметикалық және өлшенілген орта шамалар, олардың касиеттерiне тоқталыңыз

1). Орта арифметикалық шама және оның қасиеттері.

Материалды статистикалық өңдеудің негізгі мақсаттарының бірі- тәжірибеден алынған жиынтықтардың өздеріне тән ерекшеліктерін сипаттайтын көрсеткіштерін табу және оларды бір-бірімен салыстыру болып табылады.

Статистикалық жиынтықтарды екі көрсеткіш жеткілікті, толық сипаттай алады:

1. Белгінің орташа мөлшері

2. Өзгергіштік немесе шашырап бытырау (рассеяния) дәрежесі

“Белгілердің орташа мөлшері” ұғымын қарастырайық. Статистикада арифметикалық орта шама, өлшелінген орта шама, геометриялық орта шама, гармониялық орташама ұғымдары қолданылады. Биологиялық және ауылшаруашылық ғылыми-зерттеу жұмыстарында көбінесе арифметикалық орта шаманы табудың үлкен маңызы бар.

Өзінен оң және теріс ауытқуларының қосындысы нөлге тең шама – арифметикалық орта шама деп аталады. Арифметикалық орта шаманы табу үшін барлық варианттарды қосады және оларды бақылаулар санына бөледі.

Вариациялық статистикада арифметикалық орта шама М немесе ‾х (икс покрытое деп оқылады) арқылы белгіленеді.

Орта арифметикалық шаманың қасиеттері:

1) ол ортада болуы керек

2) абстракты өлшем

3) жиынтық әсерінің бірлігі – орта арифметикалық шаманы бақылау санынна көбейтеді:

∑х = х n

2) “Момент тәсілімен” орта арифметикалық шаманы есептеу.

Варианттар саны көп болған жағдайда бұл тәсілмен орта арифметикалық шаманы табу қиындау, сондықтан, оны оңай жолмен - «моменнтер тәсілін» қолдана отырып табуға болады. Ол үшін варияциалық қатардың дәл ортасында немесе ортасында жатқан вариантты шектеп алып оны шартты орта шама деп белгілейміз. Шартты орта шаманы х_о символымен белгілейді. Арифметикалық орта шаманы табу үшін шартты орта шаманың түзетпесін табу керек. Түзетпе b символымен белгіленеді және оны табу үшін оң және теріс ауытқулардың қосындысын бақылау санына (n) бөледі, кестеде көрсетілгендей::

Кластарға жіктелген вариациялық қатарлардан орта шама тапқан кезде әр кластың кездейсоқ алынған шартты орта кластан ауытқуы бірге тең деп есептелінеді. Сонан соң табылған түзетуді k немесе l әріптерімен белгіленетін класс мөлшеріне көбейтеді де, таңбасына қарай кездейсоқ шартты орта кластың шамасына не қосады, не одан алып тастайды. Кездейсоқ кластың орталық мәні W немесе х арқылы белгіленеді.

Соңыңда орта арифметикалық шаманы мына формуламен табады 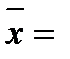x_o +(± b), кластарға жіктелген вариациялық қатарларда l көрсеткішке көбейтеді 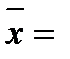x_o +(± b) х l

1). Өлшелінген орта шаманы есептеу.

Практикалық және ғылыми мақсаттар материалды зерттеуден алынған бірнеше орта шамаларды біріктіруді және осылайша біріктіру негізінде зерттелген материалдың барлығын сипаттай алатын бір жалпы орта шама табуды қажет етеді. Әрбір жеке орта шаманы табуға себепкер болған бақылаулар санын оның салмағы деп атайды.

Мынандай бір мысал қарастырайық: совхоздың алдыңғы қатарлы бригадасы 200га қыстық бидайдың әр гектарынан 60 центнерден өнім жинады. Совхоз қалған 10000 га егістіктің әр гектарынан орта есеппен 30 центнерден өнім жинады. Совхоздағы қыстық бидайдың орташа өнімділігі қандай?

200 га орта есеппен 60ц/га –ден өнім берді

10000 га 30ц/га –?

Егер орташа өнімді анықтау үшін біз арифметикалық орта шаманы пайдалансақ, онда совхоз әр гектардан (60+30): 2 =45 центнерден өнім, ал барлық егістіктен (200 га + 10000 га) х 45ц=459000 ц қыстық бидай алған болып шығады. Бұл шындыққа жанаспайды, өйткені совхоз небәрі (200х60)+(10000х30)=312000 центнер өнім жинады. Демек, 200 орта шама 60 центнердің салмағы, ал 10000 орта шама 30 центнердің салмағы болып табылады.

2) Геометриялық орташа шаманы табу.

Геометриялық орташасы – ағзалардың немесе біртұтас популяцияның өсу жылдамдығын зерттеуде қолданатын статистикалық көрсеткіш. G геометриялық орташасы аса үлкен тұрақты мөлшер және ол күндердің n санын түзудегі n дәрежелі түбірі болып табылады. Оны мына формуламен есептейміз Средняя геометрическая – статистический показатель, применяемый при изучении G = ⁿ √ 1 х 2 х 3 х…… n

G-ді қолданудың негізгі критерийлері, бұл алғашқы қасиетіне белгілі бір өлшемді арифметикалық жолмен қосу емес, керісінше пропорционалды көбею арқылы берілген белгінің өсуі болып табылады

Не нашли, что искали? Воспользуйтесь поиском: