Фактич. данные базисного периода

Ответ

Результаты статистической сводки даются обычно в виде статистических таблиц. Статистическая таблица — это рациональная форма изложения и анализа цифровых характеристик изучаемого общественного явления. В статистической таблице различают подлежащее (объект изучения) и сказуемое (числовые показатели, которыми характеризуется объект изучения) (см., например, табл. 2).

По характеру подлежащего статистические таблицы подразделяются на простые (в них содержится лишь перечень объектов), групповые (в них содержатся группы, образованные по какому-либо одному признаку) и комбинационные (в них содержатся группы, образованные по двум или более признакам).

В практике экономико-статистического анализа используются различные виды статистических таблиц, отличающихся различным числом и характером совокупностей, различным строением подлежащего и сказуемого, структурой и соотношением признаков, формирующих их.

В зависимости от структуры подлежащего и группировки в нем единиц различают статистические таблицы простые и сложные, а последние, в свою очередь, подразделяются на групповые и комбинационные.

В простой таблице в подлежащем дается простой перечень каких-либо объектов или территориальных единиц, т.е. в подлежащем нет группировки единиц совокупности. Простые таблицы бывают монографические и перечневые. Монографические таблицы характеризуют не всю совокупность единиц изучаемого объекта, а только одну какую-либо группу из него, выделенную по определенному, заранее сформированному признаку.

Т.о., простыми перечневыми таблицами называются таблицы, подлежащее которых содержит перечень единиц изучаемого объекта.

Групповыми называются статистические таблицы, подлежащее которых содержит группировку единиц совокупности по одному количественному или атрибутивному признаку. Сказуемое в групповых таблицах состоит из числа показателей, необходимых для характеристики подлежащего.

Простейшим видом групповых таблиц являются атрибутивные и вариационные ряды распределения. Групповая таблица может быть более сложной, если в сказуемом приводится не только число единиц в каждой группе, но и ряд других важных показателей, количественно и качественно характеризующих группы подлежащего. Такие таблицы часто используются в целях обобщающих показателей по группам, что позволяет делать определенные практические выводы.

Т.о., групповые таблицы позволяют выявить и охарактеризовать социально-экономические типы явлений, их структуру в зависимости только от одного признака.

Комбинационным называются статистические таблицы, подлежащее которых содержит группировку единиц совокупности одновременно по двум и более признакам: каждая из групп, построенная по одному признаку, разбивается, в свою очередь, на подгруппы по какому-либо другому признаку и т.д.

Комбинационные таблицы позволяют характеризовать типические группы, выделенные по нескольким признакам, и связь между последними. Последовательность разбиения единиц совокупности на однородные группы по признакам определяется либо важностью одного из них в их комбинации, либо порядком их излучения.

17. Статистические таблицы, их элементы, правила построения.(интеренет)

Результаты сводки и группировки материалов статистического наблюдения, как правило, представляются в виде таблиц.

Статистической называется таблица, которая содержит сводную числовую характеристику исследуемой совокупности по одному или нескольким существенным признакам, взаимосвязанным логикой экономического анализа.

Цифровой материал может быть представлен абсолютными (численность населения РФ), относительными (индексы цен на продовольственные товары) и средними (среднемесячный доход служащего коммерческого банка) величинами.

По логическому содержанию таблица представляет собой «статистическое предложение», основными элементами которого являются подлежащее и сказуемое.

Подлежащим статистической таблицы называется объект, который характеризуется цифрами. Это может быть одна или несколько совокупностей, отдельные единицы совокупности в порядке их перечня или сгруппированные по каким-либо признакам, территориальные единицы и так далее.

Сказуемое статистической таблицы образует система показателей, которыми характеризуется объект изучения, то есть подлежащее таблицы. Сказуемое формирует верхние заголовки и составляет содержание граф с логически последовательным расположением показателей слева направо.

Основные правила построения таблицы.

Статистические таблицы, как средство наглядного и компактного представления цифровой информации, должны быть статистически правильно оформлены.

1. Таблица должна быть компактной и содержать только те данные, которые непосредственно отражают исследуемое явление в статике и динамике и необходимы для познания его сущности.

2. Заголовок таблицы и названия граф и строк должны быть четкими, краткими, лаконичными, представлять собой законченное целое, органично вписывающееся в содержание текста.

3. Информация, располагаемая в столбцах (графах) таблицы, завершается итоговой строкой. Существуют различные способы соединения слагаемых граф с их итогом:

• строка «Итого» или «Всего» завершает статистическую таблицу;

• итоговая строка располагается первой строкой таблицы и соединяется с совокупностью ее слагаемых словами «В том числе».

4. Если названия отдельных граф повторяются между собой, содержат повторяющиеся термины или несут единую смысловую нагрузку, то необходимо им присвоить объединяющий заголовок.

5. Графы и строки полезно нумеровать.

6. Взаимосвязанные данные, характеризующие одну из сторон анализируемого явления целесообразно располагать в соседних друг с другом графах.

7. Графы и строки должны содержать единицы измерения, соответствующие поставленным в подлежащем и сказуемом показателям.

8. Числа целесообразнее, по возможности, округлять. Если все числа одной и той же графы или строки даны с одним десятичным знаком, а одно из чисел имеет точно два знака после запятой, то числа с одним знаком после запятой следует дополнять нулем, тем самым подчеркнув их одинаковую точность.

9. В случае необходимости дополнительной информации - разъяснений к таблице, могут даваться примечания.

18. Основные правила составления и чтения статистических таблиц.(интеренет)

Основные правила построения таблицы.

Статистические таблицы, как средство наглядного и компактного представления цифровой информации, должны быть статистически правильно оформлены.

1. Таблица должна быть компактной и содержать только те данные, которые непосредственно отражают исследуемое явление в статике и динамике и необходимы для познания его сущности.

2. Заголовок таблицы и названия граф и строк должны быть четкими, краткими, лаконичными, представлять собой законченное целое, органично вписывающееся в содержание текста.

3. Информация, располагаемая в столбцах (графах) таблицы, завершается итоговой строкой. Существуют различные способы соединения слагаемых граф с их итогом:

• строка «Итого» или «Всего» завершает статистическую таблицу;

• итоговая строка располагается первой строкой таблицы и соединяется с совокупностью ее слагаемых словами «В том числе».

4. Если названия отдельных граф повторяются между собой, содержат повторяющиеся термины или несут единую смысловую нагрузку, то необходимо им присвоить объединяющий заголовок.

5. Графы и строки полезно нумеровать.

6. Взаимосвязанные данные, характеризующие одну из сторон анализируемого явления целесообразно располагать в соседних друг с другом графах.

7. Графы и строки должны содержать единицы измерения, соответствующие поставленным в подлежащем и сказуемом показателям.

8. Числа целесообразнее, по возможности, округлять. Если все числа одной и той же графы или строки даны с одним десятичным знаком, а одно из чисел имеет точно два знака после запятой, то числа с одним знаком после запятой следует дополнять нулем, тем самым подчеркнув их одинаковую точность.

9. В случае необходимости дополнительной информации - разъяснений к таблице, могут даваться примечания.

Чтение предполагает, что исследователь, прочитав слова и числа таблицы, усвоил ее содержание, сформулировал первые суждения об объекте, уяснил назначение таблицы, понял ее содержание в целом, дал оценку явлению или процессу, описанному в таблице.

19. Статистические ряды.

Статистический ряд – ряд статистических данных, полученных в результате статистического наблюдения этих материалов. Статистические ряды могут быть упорядоченные и неупорядоченные.

Статистические ряды:

1. Ряды динамики;

a. Моментные;

b. Интервальные.

2. Ряды распределения:

a. Атрибутивные (качественные);

b. Вариационные (количественные).

Ряды динамики – простейшая группировка, основным элементом которой является частота повторений в выделенной группе.

Ряд распределения -простейшая группировка, основным элементом которой явл.чистота повторений 1цу в выделенной группе.

Атрибутивные признаки могут быть представлены географическими названиями.

В вариационном ряде число повторений изучаемой варианты называется частотой.

Вариационный ряд может быть представлен в дискретном или интервальном виде.

Все ряды могут быть представлены графически. Графические ряды распределения можно представить в виде полигона, гистограммы, огивы, кумуляты и графика Лоренца.

Полигон – величины дискретного ряда на графике, соединенные между собой отрезками.

Гистограмма – ряд сомкнутых между собой столбиков. Чаще всего гистограммы получают по интервальным данным.

Огива – если оси координат поменять местами, то есть на оси абсцисс - накопленные частоты, а на оси ординат – варианты.

График Лоренца – широко используется при характеристике концентрации производства. В таком графике определяется удельный весь не только частот, но и вариант.

20. Ряд распределения, его графическое изображение.

Ряд распределения -простейшая группировка, основным элементом которой явл.чистота повторений 1цу в выделенной группе.

Атрибутивные признаки могут быть представлены географическими названиями.

В вариационном ряде число повторений изучаемой варианты называется частотой.

Вариационный ряд может быть представлен в дискретном или интервальном виде.

Все ряды могут быть представлены графически. Графические ряды распределения можно представить в виде полигона, гистограммы, огивы, кумуляты и графика Лоренца.

Полигон – величины дискретного ряда на графике, соединенные между собой отрезками.

Гистограмма – ряд сомкнутых между собой столбиков. Чаще всего гистограммы получают по интервальным данным.

Огива – если оси координат поменять местами, то есть на оси абсцисс - накопленные частоты, а на оси ординат – варианты.

График Лоренца – широко используется при характеристике концентрации производства. В таком графике определяется удельный весь не только частот, но и вариант.

21. Статистические графики, правила оформления.(интеренет)

Статистический график - это чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков.

Значение графического метода в анализе и обобщении данных велико. Графическое изображение, прежде всего, позволяет осуществить контроль достоверности статистических показателей, так как представленные на графике они делают более очевидными имеющиеся неточности, связанные либо с наличием ошибок наблюдения, либо с сущностью изучаемого явления. При построении графического изображения должен быть соблюден ряд требований. Прежде всего, графики должны быть достаточно наглядными, так как весь смысл графического изображения как метода анализа в том и состоит, чтобы наглядно изобразить статистические показатели. Кроме того, график должен быть выразительным, доходчивым и понятным. Чтобы все эти требования выполнялись, каждый график должен включать ряд основных элементов: графический образ; поле графика; пространственные ориентиры; масштабные ориентиры; экспликацию графика

Существует множество графических изображений. В основу их классификации может быть положен ряд признаков: а) способ построения графического образа; б) геометрические знаки, изображающие статистические показатели и отношения; в) задачи, решаемые с помощью графического изображения.

По способу построения статистические графики делятся на диаграммы и статистические карты. Диаграммы - наиболее распространенный способ графических изображений. Диаграммы применяются для наглядного сопоставления в различных аспектах (пространственном, временном и др.) независимых друг от друга величин: территорий, населения и т.д.

При построении точечных диаграмм в качестве графических изображений применяются совокупности точек; при построении линейных - применяются линии. Основной принцип построения всех плоскостных диаграмм сводится к тому, что статистические величины изображаются в виде геометрических фигур и, в свою очередь, подразделяются на столбиковые, полосовые, круговые, квадратные, фигурные.

Статистические карты по графическому образу подразделяются на картограммы и картодиаграммы.

В зависимости от круга решаемых задач выделяют диаграммы сравнения, структурные диаграммы и диаграммы динамики.

На столбиковых диаграммах статистические данные изображаются в виде вытянутых по вертикали прямоугольников. Построение столбиковой требует применения вертикальной масштабной шкалы. Основания столбиков размещаются на горизонтальной линии, а высота столбиков устанавливается пропорционально изображаемым величинам. При построении столбиковых диаграмм необходимо выполнять следующие требования:

-шкала, по которой устанавливается высота столбика должна начинать с нуля;

-шкала должна быть непрерывной;

-основания столбиков должны быть равны между собой;

-наряду с разметкой шкалы соответствующими надписями следует снабжать сами столбцы.

Полосовые диаграммы состоят из прямоугольников, расположенных горизонтально. В этом случае масштабная шкала - горизонтальная ось. Принцип их построения тот же, что и в столбиковых.

Секторные диаграммы удобно строить следующим образом: вся величина явления принимается за сто процентов, рассчитываются доли отдельных частей в процентах. Круг разбивается на секторы пропорционально частям изображаемого целого. Таким образом, на 1% приходится 3,6 градуса. Для получения центральных углов секторов, изображающих доли частей целого, необходимо их процентное выражение умножить на 3,6 градуса. Секторные диаграммы позволяют не только разделить целое на части, но и сгруппировать отдельные части, давая как бы комбинированную группировку долей по двум признакам.

Секторные диаграммы выглядят убедительно при существенных различиях сравниваемых структур, а при небольших различиях она может быть недостаточно выразительна. Значительным преимуществом полосовых структурных диаграмм по сравнению с секторными является их большая емкость, возможность отразить на небольшом пространстве большой объем полезной информации.

Линейные диаграммы воспроизводят непрерывность процесса развития в виде непрерывной ломаной линии. Линейные диаграммы удобно использовать: когда целью исследования является изображение общей тенденции и характера развития явления; когда на одном графике необходимо изобразить несколько динамических рядов с целью их сравнения; когда наиболее существенным является сопоставление темпов роста, а не уровней.

Для построения линейных диаграмм используют систему прямоугольных координат. Обычно по оси абсцисс откладывается время (годы, месяцы и т.д.), а по оси ординат - размеры отображаемых явлений или процессов. На оси ординат наносят масштабы.

22. Статистический показатель, его состав, роль, функции.

Статистический показатель – обобщающая количественная характеристика признаков изучаемых явлений по совокупности в целом или по её частям в конкретных условиях места и времени.

Для несложных явлений, их характеристики можно использовать один показатель, а для сложных нужна система взаимосвязанных статистических показателей.

Функции статистического показателя:

1. Познавательная;

2. Стимулирующая;

3. Регулирующая;

4. Контрольная и другие.

Виды статистических показателей по сущности:

1. Объемные;

2. Качественные.

Виды статистических показателей по степени ограничения:

1. Индивидуальные;

2. Обобщающие.

Виды статистических показателей по характеру измеряемых явлений:

1. Моментные;

2. Интервальные.

Формы статистических показателей:

1. Абсолютные;

2. Относительные;

3. Средние;

4. Показатели вариации.

Ограничения показателя:

1. По единице измерения;

2. По объекту;

3. По времени;

4. По форме самого показателя.

23. Виды средних величин.

Средние велечины-это наиболее распространенная форма сводных показателей, которая характеризует общественные явления по одному количественному признаку.

В системе средних показателей выделяют 2 группы: степенные и структурные средние (мода, медиана) – обобщающая количественная характеристика множества индивидуальных значений варьирующего признака в пределах одного явления – качественно-однородного.

24. Средние степенные величины. Принципы их применения.

Степенные статистические средние основаны на математических средних:

- простая - взвешенная

x – осредняемая варианта;

n – число осредняемых величин;

f – определяется по сгруппированности данных;

m – степень возведения, от которой зависит вид средней.

В статистике из этого множества используется в основном 4 вида средних:

1. Квадратическая (m=2)

- простая - взвешенная

Область применения: применяется, когда в качестве вариант используются отклонения фактических значений признака от средней арифметической или от заданной нормы.

2. Арифметическая (m=1)

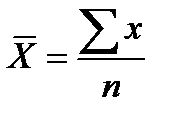- простая - взвешенная

Область применения: применяется, когда объем совокупности представляет собой сумму всех индивидуальных значений варьирующего признака. Следует отметить, что если вид средней величины не указывается, подразумевается средняя арифметическая.

3. Геометрическая (m=0)

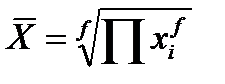- простая - взвешенная

Область применения: используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака представляют собой относительные показатели динамики, построенные в виде цепных величин, как отношения каждого уровня к предыдущему.

4. Гармоническая (m=-1)

- простая - взвешенная

Область применения: средняя арифметическая применяется для расчета среднего значения признака в тех случаях, когда известны его варианты x и их частоты f. Если статистическая информация не содержит частот f по отдельным вариантам x совокупности, а представлена как их произведение.

25. Средняя арифметическая, ее свойства.

Арифметическая (m=1)

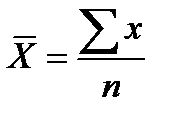- простая - взвешенная

Область применения: применяется, когда объем совокупности представляет собой сумму всех индивидуальных значений варьирующего признака. Следует отметить, что если вид средней величины не указывается, подразумевается средняя арифметическая.

Свойства средней арифметической:

1.

2.

3. Если каждую варианту разделить или умножить на какое-либо число, то средняя арифметическая уменьшится или увеличится во столько же раз.

4. Если каждую варианту уменьшить или увеличить, то средняя арифметическая уменьшится или увеличится на это же число.

5. Если все частоты разделить или умножить на какое-то число, то средняя арифметическая от этого не изменится.

26. Расчет средней по результатам группировки.(интеренет)

Данные для расчета и анализа средних величин могут быть представлены в сгруппированном виде, когда для каждого значения усредняемого признака
Х сообщается частота его повторения. В этих случаях средняя величина рассчитывается по обычным формулам средних взвешенных (арифметических либо гармонических). Если в сгруппированных данных указывается не конкретное значение признака
Х по каждой группе, а лишь интервал его изменения, то в этом случае необходимо получить среднее значение признака по каждой группе. А далее используются обычные формулы средних взвешенных. Если же средние значения признака в группах определить по имеющимся сведениям нельзя, то их заменяют условно значениями центра интервалов. В результате получают ряд распределения, аналогичный дискретному, где в качестве значений дискретного признака будут выступать центры интервалов аi,а в качестве весов признака Fi
- количество элементов ряда для интервала i.
Таким образом, расчет средней арифметической делают по формуле
Показательсебестоимостиявляется вторичным признаком, так как он задан на единицу первичного признака (объем продукции, выраженный абсолютной величиной) и может быть представлен как отношение двух первичных признаков, а именнозатрат на производствоиобъём продукции:
С = ЗП / ОП, где С — себестоимость, ЗП — затраты на производство, ОП —.объем продукции.
Следовательно, для расчета средней себестоимости по каждому предприятию следует вычислить среднюю взвешенную. Нужно выбрать: арифметическую или гармоническую?
Выбор вида средней усредняемого признака выполняется по следующим правилам.
1. Если в условии задачи даны численные значения числителя и знаменателя логической формулы показателя, средняя величина вычисляется непосредственно по этой формуле.
2. Если имеется ряд данных по двум взаимосвязанным показателям, для одного из которых нужно вычислить среднюю величину, и при этом известны численные значения знаменателяеёлогической формулы, а значения числителя не известны, но могут быть найдены как произведения этих показателей, то средняя должная вычисляться по формулесредней арифметической взвешенной.
3. Если известны численные значения числителя логической формулы, а значения знаменателя не известны, но могут быть найдены как частное от деления одного показателя на другой, то средняя вычисляется по формулесредней гармонической.
Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности — носители признака, а произведения этих единиц на значения признака (т. е. m = X*f). К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т. д.) предприятиям, рабочим, занятым изготовлением одного итого же вида продукции, одной и той же детали, изделия.
Общее требование к формуле расчета среднего значения состоит в том, чтобы все этапы расчета имели реальное содержательное значение. Полученное среднее значение должно заменить индивидуальные значения признака у каждого объекта без нарушения связи индивидуальных и сводных показателей. Иначе говоря, средняя величина должна исчисляться так, чтобы при замене каждого индивидуального значения усредняемого показателя его средней величиной оставался без изменения некоторый итоговый сводный показатель, связанный с усредняемым. Этот итоговый показатель является определяющим в том смысле, что его связь с индивидуальным значением признака определяет способ расчета средней величины.

27. Структурные средние, их использование в статистике.

Наиболее распространенными среди структурных средних являются мода и медиана.

Мода – величина признака, которая наиболее часто встречается в данной совокупности.

Если признак, по которому определяется модальное значение, представлен интервалом, то конкретное значение моды определим по формуле Орджетцкого.

, где:

X₀ - нижняя граница модального интервала;

i - шаг интервала;

f₁ - частота предмодального интервала;

f₂ - частота модального интервала;

f₃ - частота послемодального интервала.

Мода дает возможность определить преобладающий исследуемый уровень в данный момент.

Если в распределении 2 варианты имеют общую частоту, то такое распределение мультимодальное. Мультимодальное распределение характерно для неоднородной совокупности.

Если интервальный ряд представлен неравными интервалами, то применяется плотность распределения – рассчитывается как частное отделение частоты на величину принятого интервала.

Медиана – признак, характеризующий варианту, стоящую в середине ранжированного вариационного ряда. Положение медианты определяется ей номером. Номер медианы определяется следующим образом:

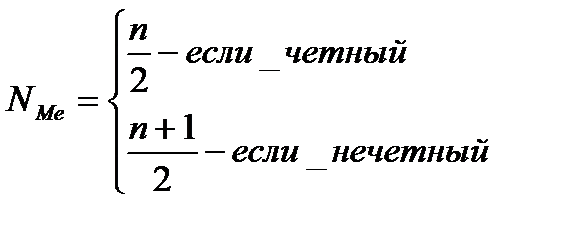
В дискретном ряду, медиана определяется по накопленным частотам.

В интервальных вариационных рядах сначала по накопленным частотам определяется интервал, в котором она находится, а затем по форму Орджетцкого определяется конкретное значение медианы.

, где:

- нижняя граница медианного интервала;

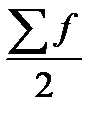- номер медианы;

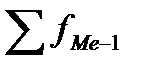-накопленная частота предмедианного интервала;

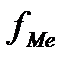- частота медианного интервала.

Медиана обладает следующим свойством: сумма отклонения каждого члена ряда от медианы является наименьшей величиной. Благодаря этому свойству, медиану используют при оптимизации каких-либо процессов.

Наряду с медианой для характеристики структуры используются квартири и децири. Квартири делят ряд по сумме накопленных частот на 4 равные части, а децири на 10 равных частей.

Медиана может быть использована вместо средней величины, если имеет место рассеивание совокупности по краям вариационного ряда.

28. Взаимосвязь абсолютных и относительных величин, их комплексное использование.

29. Виды относительных величин, взаимосвязь.

Абсолютной величиной называется показатель, выражающий размеры социально-экономического явления.

Относительной величиной в статистике называется показатель, выражающий количественное соотношение между явлениями. Он получается в результате деления одной абсолютной величины на другую абсолютную величину. Величина с которой мы производим сравнения называется основанием или базой сравнения.

Абсолютные величины - всегда величины именованные.

Относительные величины выражаются в коэффициентах, процентах, промили и т.д.

Относительная величина показывает, во сколько раз, или на сколько процентов сравниваемая величина больше или меньше базы сравнения.

В статистике различают 8 видов относительных величин:

1. Относительная величина выполнения плана (ОВВП) показывает во сколько раз или на сколько процентов выполнено данное задание.

ОВВП= фактические данные отчетного периода

плановые данные отчетного периода

2. Относительная величина планового задания (ОВПЗ) показывает во сколько раз или на сколько процентов плановое задание отчетного периода больше или меньше уровня базисного периода.

ОВПЗ= плановое число отчетного периода

фактич. данные базисного периода

3. Относительная величина динамики (ОВД) показывает во сколько раз или на сколько процентов уровень отчетного периода больше или меньше уровня базисного периода.

ОВД= фактич. данные отчетного периода

Не нашли, что искали? Воспользуйтесь поиском: