среднегодовая численность населения

30. Показатели асимметрии и эксцесса, их назначение.(можешь почитать но надо что то другое искать,более краткое..)

Любое реальное распределение можно изобразить схематически в виде кривой, воспроизводящей основные особенности данного распределения. Под кривой распределения понимается графическое изображение в виде непрерывной линии изменения частот, функционально связанных с изменением вариант.

Элементами распределения являются:

• варианта
• частота

В зависимости от вида кривых, изображающих распределение, выделяют несколько основных типов распределения:

• одновершинные
• многовершинные

К одновершинным относятся те, в которых один, обычно центральный вариант, имеет наибольшую частоту (плотность распределения). Частоты же остальных вариантов убывают по мере удаления от центрального.

Если частоты убывают слева и справа от центрального значения одинаково, то такие распределения называются симметричными.

Если частоты убывают слева и справа от центра распределения с разной скоростью, то такие распределения называют асимметричными.

Многовершинные распределения – это распределения, в которых несколько центров, т. е. такие, у которых несколько максимумов частот.

Для однородных совокупностей, как правило, характерны одновершинные распределения.

Многовершинность распределения свидетельствует о неоднородности изучаемого явления. В этом случае необходимо произвести перегруппировку данных с целью выделения более однородных групп.

Выяснение общего характера распределения предполагает, наряду с оценкой его однородности, вычисление показателей асимметрии и эксцесса.

Кривые распределения бывают:

1. симметричными
2. асимметричными.

В зависимости от того, какая ветвь кривой распределения вытянута, различают:

1. правостороннюю асимметрию
2. левостороннюю асимметрию.

Для характеристики степени асимметрии двух или нескольких рядов пользуются коэффициентом асимметрии.

Для одновершинных распределений:

Более точным является коэффициент асимметрии, рассчитанный как отношение центрального момента третьего порядка (μ³) к среднеквадратическому отклонению в 3-й степени (Ϭ³):

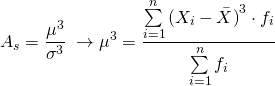
1. Для симметричного распределения:

Соответственно, в симметричном распределении центральный момент 3-го порядка равен нулю (μ³=0), т. е. алгебраическая сумма отклонений отдельных значений признака (вариант), расположенных слева и справа от средней, равна нулю. График симметричного распределения симметричен относительно точки максимума.

Для несимметричных распределений центральные моменты нечетного порядка отличны от нуля:

2. Асимметрия положительна (A_s>0), если длинная часть кривой распределения расположена справа от моды (М_о). В этом случае соотношение между средней, медианой и модой нарушено:

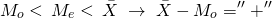
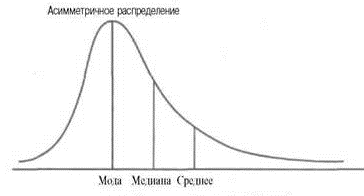
3. Асимметрия отрицательна (A_s<0), если длинная часть кривой распределения расположена слева от моды (М_о).

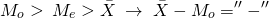
A_s< 0.25 – слабая асимметрия

A_s= 0.25-0.5 – умеренная асимметрия

A_s> 0.5 – крайне асимметричное распределение

Для оценки «крутизны» (островершинности) распределения пользуются характеристикой – эксцессом.

Коэффициент эксцесса:

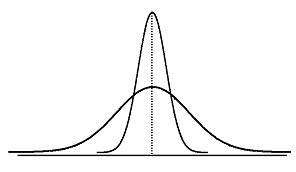
1. Для нормального распределения:

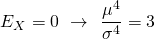
2. Выше нормального (островершинное распределение):

3. Ниже нормального (плосковершинное распределение):

Стр.138

31. Показатели вариации количественного признака, их роль.

32. Вариация признаков, способы ее изучения, критерии оценки.

33. Виды дисперсий. Правило сложения дисперсий.

Правило сложений дисперсий:

Для проведения факторного анализа возможно использование различных видов дисперсий:

1. Общая: 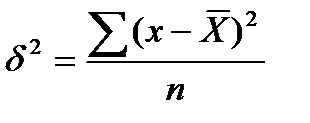- простая 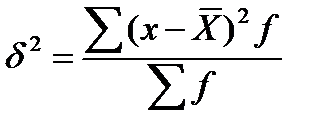- взвешенная Общая дисперсия улавливает влияние группы факторов:

a. Положенного в основу группировки – систематический фактор;

b. Случайной причины – оказывающей влияние на результат.

Таким образом, с помощью дисперсионного анализа можно выявить влияние систематического фактора и случайных величин на результат, а также оценить тесноту связи между фактором, положенным в основу группировки и результатом.

2. Межгрупповая дисперсия: выражает величину, обусловленную влиянием признака, положенного в основу группировки, выражает влияние систематического фактора.

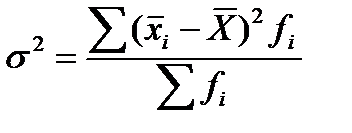, где:
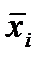- среднее значение факторного признака, положенного в основу группировки по отдельно взятой группе;

- среднее значение факторного признака в целом по совокупности;

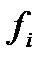-частота повторения в соответствующей группе.

3. Средняя внутригрупповая дисперсия – устанавливает влияние случайных величин.

- внутригрупповая дисперсия

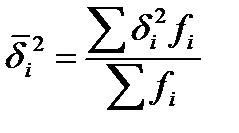- средняя внутригрупповая дисперсия

Правило сложения дисперсий:

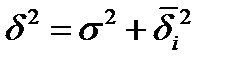Если признак, положенный в основу группировки оказывает сильное влияние на результат, то значение межгрупповой дисперсии приближается к общей дисперсии и наоборот.

В

34. Определение необходимой численности выборки.

35. Разработка данных выборочного наблюдения.

36. Малая выборка, ее особенности

37. Собственно-случайный механический отбор.

38. Ошибки выборочного наблюдения, методика расчета.

В ходе выборочного наблюдения, возникают ошибки репрезентативности, которые характерны только для выборочного наблюдения: бывают случайными и систематическими.

Систематические ошибки возникают по вполне определенной причине, связанной с механизмом процесса отбора. Такие ошибки невозможно исправить, результат не будет отвечать требованиям, в следствие этого, процедуру отбора следует начать заново.

Случайные ошибки: при выборочном наблюдении связаны не только с регистрацией фактов, но и с характерной для выборки ошибки, связанной с расхождением в структуре выборочной и генеральной совокупности. В связи с этим расхождением в структуре и генеральной совокупности, возникает необходимость расчета показателя предельной ошибки выработки () которая затем учитывается при распространении полученного результата на генеральную совокупность.

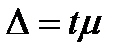, где: 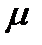- средняя ошибка выборки; - коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной вероятности. Вероятность задается самим исследователем.

Величина средней ошибки выборки зависит от способа отбора, которому соответствует определенный вид дисперсии, и от того, повторный отбор или бесповторный.

Ошибки отборов:

1. Случайный отбор:

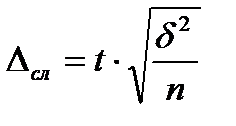- повторный 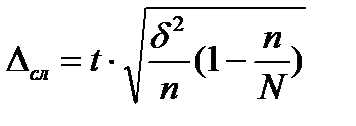- бесповторный

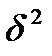- дисперсия выборочной совокупности (общая).

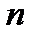- число отобранных единиц.

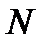- число единиц в генеральной совокупности.

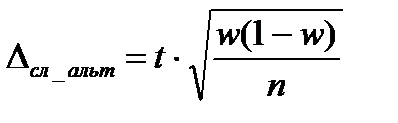- повторный

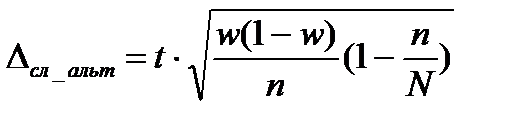- бесповторный

2. Механический отбор: повторного механического отбора не бывает.

- бесповторный

3. Типический отбор – связан с механическим отбором по неоднородной совокупности, поэтому прежде чем проводить отбор, необходимо разбить генеральную совокупность на однородные типические группы; дисперсия средняя внутригрупповая:

- повторный - бесповторный

4. Серийный отбор: дисперсия межгрупповая.

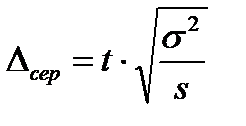- повторный - бесповторный

s – число отобранных серий;

S – число серий генеральной совокупности.

39. Методы сглаживания динамических рядов.

40. Методы расчета средних в динамических рядах.

41. Приемы приведения рядов динамики и сопоставимому виду.

42. Виды рядов динамики. Правила их построения.

43. Аналитические показатели рядов динамики, их взаимосвязь.

44. Аналитическое выравнивание динамических рядов.

45. Приемы обработки и анализа динамических рядов.

46. Анализ уровней и темпов развития экономических явлений.

47. Анализ сезонных колебаний.

48. Экстраполяция и интерполяция динамических рядов.

Интерполяция – расчет недостающего уровня динамического ряда, расположенного внутри него.

Методы интерполяции:

1.

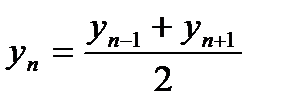
2.

3.

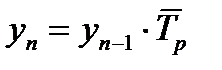
4.

5. По формуле аналитического выравнивания.

Экстраполяция – приблизительный расчет недостающего уровня динамического ряда, расположенного по его краям: в сторону прошлого – ретроспективный, в сторону будущего – перспективный.

Для экстраполяции возможно применение (2)-(5) методов интерполяции.

49. Индексы, их сущность. Виды индексов.

50. Агрегатный индекс как основная форма свободного индекса.

51. Индексный анализ взвешенной средней.

52. Правила фиксирования веса в индексных моделях.

53. Формы сводных индексов.

54. Индексы цепные и базисные, с постоянными и переменными весами.

55. Показатели эластичности.

56. Взаимосвязь индексов в их комплексное использование.

57. Индексы цен и объема продукции.

58. Территориальные индексы.

59. Показатели тесноты связи в статистическом анализе.

Не нашли, что искали? Воспользуйтесь поиском: