Неупругое соударение

 Если
m₁ –массапервого тела,
m₂ − масса второго тела,
v₁ − скорость первого тела до соударения,
v₂ − скорость второго тела до соударения,
v − общая скорость обоих тел после соударения,
то, согласно формуле закона сохранения импульса

Следует, что

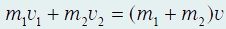
и

 Согласно закону сохранения энергии кинетическая энергия системы после соударения меньше, чем до него, так как часть энергии расходуется на неупругую деформацию тел.
 Если
W₁ − сумма кинетических энергий обоих тел до соударения,
W₂ − сумма кинетических энергий обоих тел после соударения,
ΔW − потеря энергии, равная работе, затраченной на деформацию, то, согласно закону изменения кинетической энергии

а

 Подставив в это равенство выражение (3) для v преобразовав его, получим выражение для работы, затраченной на деформацию:

13. Момент инерции материальной точки твердого тела
Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело

(5.4)

В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами , и моменты инерции тела определяется интегралом

(5.5)

о где - расстояние от элемента до оси вращения.

Распределение массы в пределах тела можно охарактеризовать с помощью
плотности

(5.5)

где m - масса однородного тела, V - его объем. Для тела с неравномерно распределенной массой это выражение даетсреднюю плотность.

Плотность в данной точке в этом случае определяется следующим образом

и тогда

(5.6)

Пределы интегрирования зависят от формы и размеров тела Интегрирование уравнения (5.5) наиболее просто осуществить для тех случаев, когда ось вращения проходит через центр тяжести тела. Рассмотрим результаты интегрирования для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.

Момент инерции полого цилиндра с тонкими стенками, радиуса R.

Для полого цилиндра с тонкими стенками

Сплошной однородный диск. Ось вращения является осью диска радиуса . и массы m с плотностью Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки 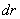и массой . Для него

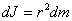
Весь диск можно разбить на бесконечное множество цилиндров, а затем просуммировать:

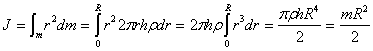
Момент инерции шара относительно оси, проходящей через центр тяжести.

14.Момент инерции однородного стержня В общем случае моменты инерции различных тел можно найти по формуле I=mmR2, где m - коэффициент пропорциональности, который зависит от формы тела и его расположения относительно оси вращения. Найдем момент инерции однородного стержня относительно оси, проходящей через один из его концов, перпендикулярно продольной геометрической оси симметрии (рис. 5.2). Рис. 5.2   Пусть ось вращения ВВ проходит через правый конец стержня (точка Г), тогда I=mmL2, где L - длина стержня. Согласно теореме Штейнера имеем . Величину момента инерции Ic относительно оси, проходящей через центр масс (точка С), представим как сумму моментов инерции двух стержней с длинами ДС=СГ=L/2 и массой каждого, равной m/2 стержня, т.е.   .   Подставим значения момента инерции I и Ic в формулу теоремы Штейнера и найдем m: . После преобразования получим, что m = 1/3. Следовательно, момент инерции стержня относительно оси, проходящей через центр масс,   (5.6) а относительно оси ВВ,   15. Теоре́ма Гю́йгенса — Ште́йнера (теорема Гюйгенса, теорема Штейнера): момент инерции тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела 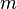на квадрат расстояния 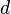между осями[1]: 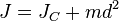где — известный момент инерции относительно оси, проходящей через центр масс тела, — искомый момент инерции относительно параллельной оси, — масса тела, — расстояние между указанными осями. Теорема названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса Вывод Будем рассматривать абсолютно твёрдое тело, образованное совокупностью материальных точек[2]. 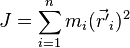По определению момента инерции для и можно записать , где 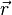— радиус-вектор точки тела в системе координат с началом, расположенным в центре масс, а — радиус-вектор точки в новой системе координат, через начало которой проходит новая ось. 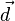Радиус-вектор можно расписать как сумму двух векторов: , где — радиус-вектор расстояния между старой и новой (проходящей через центр масс) осями вращения. Тогда выражение для момента инерции примет вид: 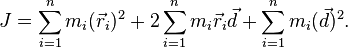Вынося за сумму , получим: По определению центра масс для его радиус-вектора выполняется Поскольку в системе координат с началом, расположенном в центре масс, радиус-вектор центра масс равен нулю, то равна нулю и сумма . Тогда: Откуда и следует искомая формула: , где — известный момент инерции относительно оси, проходящей через центр масс тела. Если тело состоит не из материальных точек, а образовано непрерывно распределённой массой, то во всех приведённых выше формулах суммирование заменяется интегрированием. Ход рассуждения при этом остаётся прежним.Следствие. Из полученной формулы очевидно, что Поэтому можно утверждать: момент инерции тела относительно оси, проходящей через центр масс тела, является наименьшим среди всех моментов инерции тела относительно осей, имеющих данное направление.

Не нашли, что искали? Воспользуйтесь поиском: