О математике в древней Индии

by КОЛПАКОВ А.Н. on 4 ИЮЛЯ 2011

Индия имеет большую и богатую самобытную культуру, начало которой уходит в седую древность. Много тысяч лет тому наза, еще до нашей эры, в Индии городские водосточные системы и оросительные каналы, строились многоэтажные здания из хорошо обожженного кирпича. В далеком прошлом индийцы владели искусством керамического производства (производство изделий обожженной глины), умело пользовались гончарным кругом, успешно развивали ювелирное дело (изготовление изделий из драгоценных камней и металлов).

Еще в глубокой древности Индия славилась знаниями в области астрономии, грамматики и других наук.

Наибольших успехов Индийские ученые достигли в области математики. Они явились основоположниками арифметики и алгебры, в разработке которых пошли дальше греков.

Величайшим достижением древнеиндийской математики является, прежде всего, открытие позиционной системы счисления, состоящей из десяти индийских цифр, включая и знак нуль, называемый по-индийски «сунья», что дословно означает «ничто». Интересно заметить, что в первоначальном начертании нуль изображался точкой и лишь спустя много веков – в виде маленького кружка. Кто первый из индийских ученых стал употреблять десятичную систему, неизвестно точно. Однако есть основание думать, что эта система была изобретена в начале первого века нашей эры. Что касается первого употребления знаку нуля, то это факт относится ко второму веку нашей эры.

Наиболее известными индийскими математиками являются Ариабхата (конец 1 века), Брахмагупта (7 век) и Бхаскара (12 век).

Индийские математики далекого прошлого любили состязаться на публичных народных собраниях. По этому поводу один индийский автор 7 века, заканчивая свою книгу, писал: «Подобно тому, как солнце затмевает своим блеском звезды, так мудрец затмевает славу других людей, предлагая и особенно решая на народных собраниях математические задачи».

Заметим, что все указания и решения к индийским задачам даются сейчас в современной символике.

Задачи древней Индии:

1) Из четырех жертвователей второй дал вдвое больше первого. Третий дал втрое больше первого, четвертый в четверо больше первого, а все вместе они дали 132 монеты. Сколько монет дал первый.

Эта задача взята из бахшалийской рукописи, найденной в 1881 году при раскопках в Бахшали в северо-западной Индии. Рукопись выполнена на березовой коре и относиться к 3-му или 4-му веку нашей эры. Ученые-математики установили, что эта рукопись является неполной копией боле древних математических рукописей.

2) Пятая часть пчелиного роя села на цветок кадамба, Треть — на цветокх силиндха. Утроенная разность последних двух чисел пчел направилась к цветам кутая и осталась еще одна маленькая пчелка, летающая взад и вперед, привлеченная ароматом жасмина и пандуса. Спрашивается, сколько всего пчел.

Задача присутствует в трактате «сущность вычисления» («Ганитасара») индийского математика Сридхары, жившего в промежутке 7-10 в.в. Время жизни точно не установлено. (Сридхара является автором ряда задач, которые широко использовались индийскими математиками последующих времен.

3) Два светила находятся на данном расстоянии (d) друг от друга, движутся одно к другому с данными скоростям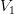и и 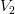. Определить точку их встречи.

Задача взята из трактата «Ариабхатиам» известного индийского математика конца 5-го – начала 6-го века Ариабхаты. Этот трактат посвящен астрономии и математике. В его математической части Ариабхата дает ряд правил по арифметики, алгебре, геометрии и тригонометрии, нужных для астрономии и в первую очередь составления астрономических страниц. Ариабхата является автором многих задач по элементарной математике, одна из которых и приводится.

Развитие индийской математики

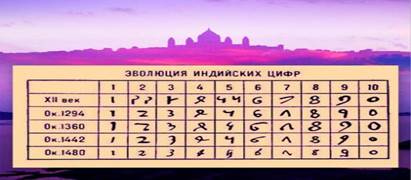
Развитие математики как науки в каждой древней цивилизации начиналось со счета. Он был неотъемлемой частью эволюции всего человечества. С помощью математического счета человек вел хозяйство, контролировал поголовье скота, производил расчет календаря, вел торговлю и т.п. Параллельно социуму развивалась и математика, которая начала свое движение со счета. Нельзя не отметить индийский способ записи чисел, который отличался некоторой изысканностью. Изначально для нумерации использовалась сиро-финикийская методика, а с шестого века до н.э. стали применять написание «брахми», с отдельными символами для цифр «1-9», которые после небольших видоизменений дошли до нас и называются «арабскими».

Не нашли, что искали? Воспользуйтесь поиском: