ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ ФИЗИЧЕСКИХ ВЕЛИЧИН

Некоторые величины не могут быть определены непосредственно с помощью технических устройств (по ряду причин, которые здесь не рассматриваются) и их значения приходится рассчитывать на основе известной зависимости между этой величиной и величинами, определяемыми из опыта. Такие измерения принято считать косвенными

При выполнении косвенных измерений необходимо оценить как результат измерения некой величины W, так и его абсолютную погрешность D W.

Допустим, что определяемая величина W является функцией других измеряемых величин, например, X, Y, Z …, полученных в результате прямых измерений, т. е. W = f (X, Y, Z …).

При этом можно поступать двояким образом. Но как бы мы не поступали, если измерения выполнены и обработаны правильно, то результат расчета должен быть одинаковым.

1. Способ определения абсолютной погрешности
по аналогии с прямыми измерениями

Он фактически повторяет метод прямых измерений, рассмотренный в главе 2, что видно из следующих действий:

1. Выполнить n наблюдений. В каждом наблюдении определить величины X_i, Y_i, Z_i , …, где i – номер наблюдения и по рабочей формуле вычислить

2. В качестве оценки результата измерений выбрать величину:

3. Найти среднее квадратичное отклонение результата расчета:

4. Определить доверительный интервал отклонения искомого значения величины W по формуле:

,

где – коэффициент Стьюдента.

5. Записать результат расчета в виде:

В этом случае величину доверительной вероятности Р определяют, исходя из правил, рассмотренных в главе 2.

2. Способ определения абсолютной погрешности
на основе использования первых производных от функции

1. Получить оценки результатов прямых измерений определяющих величин и их погрешностей:

.

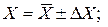
2. По результатам прямых измерений , вычислить :

3. Найти оценку погрешности D W, основываясь на рабочей формуле W = f (X, Y, Z …) и используя формулу погрешности, связывающую D W с погрешностью прямых измерений:

При расчете величины D W возможны случаи, когда искомая величина является функцией одной или нескольких переменных. Рассмотрим их в этой последовательности.

Случай одной переменной. Напомним, что согласно правилам математического анализа для любой функции W = f (X) и любого достаточно малого приращения аргумента D X (рис. 1) можно записать:

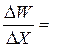
(W),

где (W) – первая производная от функции W (X).

Из этого следует, что приращение функции равно:

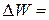
(W) D X.

Итак, чтобы найти погрешность величины , следует вычислить производную (W) и умножить ее на погрешность

Рис. 1. График функции одной переменной W (X)

Случай нескольких переменных. Для этого введено понятие частной погрешности величины по аргументу:

Здесь – так называемая частная производная от f (W) по Х, она вычисляется так, будто в исходной формуле все аргументы (кроме Х) постоянные величины. Измерения отдельных физических величин (и их погрешности) считаются независимыми. Поэтому можно считать независимыми их частные погрешности и применять закон сложения погрешностей:

Заметим также, что на основе этого выражения, предварительно возведя его в квадрат и поделив на , можно определить относительную погрешность величины W:

Так как то для относительной погрешности
получаем

4. Записать результат расчета в виде:

В этом случае величину доверительной вероятности Р, как и в первом способе, определяют, исходя из прежних правил, рассмотренных
в главе 2.

Поскольку зависимости искомой функции от нескольких аргументов бывают очень сложными, то и сама процедура нахождения их частных производных, а затем и абсолютной погрешности, тоже не проста. Их устранение возможно на основе расчета абсолютной погрешности по величине относительной погрешности, что и представлено далее.

3. Способ определения абсолютной погрешности
на основе ее относительной величины

Возведя предыдущее выражение

в квадрат и поделив на , можно определить относительную погрешность 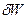величины W:

Поскольку ,
то

Зная из математики, что относительную погрешность можно выразить следующим образом

Этот прием позволяет упростить процедуру расчета, поскольку достаточно знать правила нахождения первых производных не от всех возможных функций, а только от логарифмической функции. Поскольку известно, что в случае линейной функции

, ,

то получим

здесь Х, Y – среднеарифметические значения.

Если логарифмируемые функции будут степенными, то необходимо учесть этот факт введением показателя степени, т. е. умножить производную на его значение. Тогда получим:

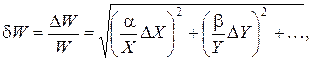
где a и b – показатели степени соответствующих функций.

Таким образом, из последнего уравнения следует, что для нахождения относительной погрешности косвенных измерений достаточно знать средние значения и абсолютные погрешности величин, определенных в процедуре прямых измерений. Затем найдем абсолютную погрешность:

D W = W .

Заметим, что этот прием справедлив для тех случаев, когда искомая функция представлена произведением соответствующих аргументов с некоторыми показателями степени.

Рассмотрим пример применения рассмотренного способа.

Пусть известно, что некоторая величина Q связана с другими величинами зависимостью:

Q = .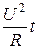

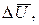
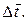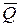В ходе прямых измерений получены значения Найти и .

Численное значение 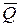находим подстановкой средних значений в исходное уравнение.

Далее находим относительную погрешность Q, пользуясь ранее полученной формулой:

В этом уравнении величины Х, Y и другие следует заменить на конкретные значения согласно поставленной задаче, тогда получим:

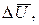
Подставив в это уравнение значения найдем 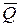и затем .

Следует обратить внимание на соблюдение правила размерностей физических величин при их сложении. Они должны быть представлены либо все в абсолютных единицах, либо все в относительных единицах. Смешение их недопустимо, результат будет неправильным.

Задачи и вопросы для самоконтроля

1. Курсант измеряет две величины a и b и получает a = 11,5±0,2 см и b = 25,4±0,2 см. Затем он вычисляет произведение q=ab. Получите его ответ и приведите абсолютное значение погрешности, а также погрешность в процентах.

2. Курсант получил следующие результаты измерения: a = 5±1 см; b =18±2 см; с = 12±1 см; t = 3,0±0,5 с; т = 18±1 г. Вычислите следующие величины, их погрешности и относительную погрешность в процентах: a+b+c; a+b-c; 4 a; (где цифры 4 и 2 не содержат погрешности) и

3. Если найдено, что t = 8,0±0,5 с, то каковы значения и погрешности t ², 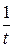и ?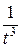

4. Посетитель средневекового замка решает определить глубину колодца, измеряя время падения брошенного в него камня. Он определяет, что время падения равно t = 3,0±0,5 с. Какой вывод он сделает о глубине колодца?

5. Частная производная от q (x, y получается дифференцированием функции q по х, когда y считается постоянным. Найдите частные производные и для трех функций: а) q (x, y) =x+y, б) q (x, y) = xy, в) q (x, y) = x ² y ².

ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ

При выполнении индивидуальных заданий следует руководство-
ваться следующими указаниями:

1. Номер варианта индивидуального задания соответствует двум последним цифрам служебного удостоверения обучаемого (или зачетной книжки – для лиц, не имеющих специального звания).

2. Численные значения рассчитываемых физических величин, необходимые для выполнения индивидуального расчетно-графического задания, принимают из соответствующих таблиц в зависимости от номера варианта, принятого согласно п. 1.

3. Индивидуальные задания выполнить в отдельной тетради, четким разборчивым почерком, при этом в тетради должны быть поля,
а страницы пронумерованы.

4. Графики выполнить на миллиметровой бумаге и вклеить в тетрадь с выполненным заданием.

5. При использовании уравнений, табличных значений и других справочных данных должны быть:

· ссылки на источник заимствования (название источника и автор, страница, номер уравнения, номер таблицы и др.);

· разъяснения по выполняемым операциям (исходное уравнение, математические преобразования, подстановка расчетных значений вместе с единицами измерения, ответ в виде числа, его погрешности, единицы измерения и доверительной вероятности).

6. Выполненное задание должно быть представлено преподавателю на проверку в установленный срок.

Задача 1

Проведены испытания однотипных противопожарных преград и измерены (во времени) значения предела их огнестойкости T. Результаты представлены в табл. 1.1.

Найти среднее значение предела огнестойкости и случайную ошибку. Систематической ошибкой пренебречь. Доверительная вероятность указана в табл. 1.

Из табл. 1 выбрать для обработки результаты измерений в соответствии с табл. 3.

Таблица 1

Не нашли, что искали? Воспользуйтесь поиском: