Общий вид и свойства системы уравнений

СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Это один из основных разделов в алгебре. Нет такой отрасли науки и приложений, где в том или ином виде не использовались бы системы линейных алгебраических уравнений. При решении экономических задач системы линейных уравнений наиболее употребимы как в аппарате исследования, так и при рассмотрении частных проблем.

Основные понятия

Общий вид и свойства системы уравнений

Система т линейных уравнений с п неизвестными (переменными) х ₁, х ₂, …, x_n имеет вид

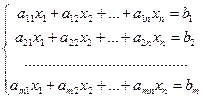
(16.1)

Здесь a_ij и b_j — произвольные числа (i = 1, 2,..., m; j = 1, 2,..., n), которые называются соответственно коэффициентами при неизвестных и свободными членами уравнений (16.1). Первый индекс у коэффициентов при неизвестных означает номер уравнения, второй индекс соответствует номеру неизвестного x_i/

Решением системы уравнений (16.1) называется набор п чисел 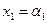, , …, ,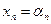приподстановке которых в эту систему каждое уравнение данной системы превращается в тождество.

Система уравнений (16.1) называется совместной, если она имеет хотя бы одно решение; если система не имеет решений, она называется несовместной. Совместная система уравнений имеет либо одно решение, и в таком случае она называется определенной, либо, если у нее больше одного решения, она называется неопределенной.

Системы уравнений вида (16.1) называются эквивалентными, если они имеют одно и то же множество решений. Элементарные преобразования исходной системы приводят к эквивалентной системе. К элементарным преобразованиям относятся:

1) вычеркивание уравнения 0 х ₁+ 0 x ₂ + … + 0 x_n = 0 - нулевой строки;

2) перестановка уравнений или слагаемых a_ijx_j в уравнениях;

3) прибавление к обеим частям одного уравнения соответственно обеих частей другого уравнения этой системы, умноженного на любое действительное число;

4) удаление уравнений, являющихся линейными комбинациями других уравнений системы.

Последнее свойство вытекает из третьего свойства: если какое-либо уравнение представляет собой линейную комбинацию других уравнений, то из него можно сформировать нулевую строку.

Не нашли, что искали? Воспользуйтесь поиском: