
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теплообмен в паровом котле
Теплообмен в топке. Топка представляет собой замкнутую камеру для сжигания топлива и одновременно теплообменный аппарат для передачи теплоты парообразующим поверхностям нагрева, расположенным в ней.
Передача теплоты в топке осуществляется излучением (радиацией). Телом, излучающим теплоту, является факел (пламя), а телом, воспринимающим лучистую теплоту, – парообразующие трубы, расположенные по боковым стенкам топки (Рис. 3.4). В процессе передачи теплоты парообразующим трубам факел, состоящий из горячих продуктов сгорания и мельчайших частичек сажи и золы, охлаждается. При этом его температура снижается от максимальной (теоретической), обозначаемой h 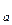 , °С (
, °С ( , К), до температуры на выходе из топки (за топкой), обозначаемой h
, К), до температуры на выходе из топки (за топкой), обозначаемой h 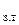 , °С (
, °С (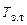 , К).
, К).
А-А
 Рис. 3.4. Схема топки парового котла:
1 – топочная камера; 2 – факел; 3 – лучевоспринимающая поверхность экранного ряда (экрана); 4 – кирпичная обмуровка переднего фронта; 5 – лучевоспринимающая поверхность испарительного притопочного пучка труб; 6 – кирпичная обмуровка заднего фронта
Рис. 3.4. Схема топки парового котла:
1 – топочная камера; 2 – факел; 3 – лучевоспринимающая поверхность экранного ряда (экрана); 4 – кирпичная обмуровка переднего фронта; 5 – лучевоспринимающая поверхность испарительного притопочного пучка труб; 6 – кирпичная обмуровка заднего фронта
|
Пусть энтальпия газов при теоретической температуре равна  , МДж/кг, а энтальпия газов при температуре за топкой равна
, МДж/кг, а энтальпия газов при температуре за топкой равна  , МДж/кг. Тогда количество теплоты, которое передается в топке излучением в единицу времени, составит, МВт,
, МДж/кг. Тогда количество теплоты, которое передается в топке излучением в единицу времени, составит, МВт,
 . .
| (3.22) |
Чтобы найти  , надо вначале определить
, надо вначале определить  и
и  . Что касается энтальпии
. Что касается энтальпии  , то ее определить нетрудно. Такую энтальпию (максимально возможную) газы получили бы, если бы горение происходило в топке без теплообмена факела с поверхностями нагрева (из-за отсутствия последних). Тогда вся выделившаяся теплота перейдет в энтальпию газов (адиабатное горение).
, то ее определить нетрудно. Такую энтальпию (максимально возможную) газы получили бы, если бы горение происходило в топке без теплообмена факела с поверхностями нагрева (из-за отсутствия последних). Тогда вся выделившаяся теплота перейдет в энтальпию газов (адиабатное горение).
При сжигании топлива в адиабатной топке теоретическая энтальпия газов будет равна всему полезному тепловыделению в топке. Следовательно, ее можно определить по формуле, МДж/кг,
 , ,
| (3.23) |
| где | 
| – | энтальпия воздуха, подаваемого в топку для горения, МДж/кг; |

| – | температура воздуха, подаваемого в топку, °С. |
Зная  и коэффициент избытка воздуха ее, можно, пользуясь диаграммой I – h, определить теоретическую (адиабатную) температуру горения h
и коэффициент избытка воздуха ее, можно, пользуясь диаграммой I – h, определить теоретическую (адиабатную) температуру горения h 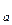 , °С,
, °С,  = h
= h 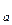 + 273, К.
+ 273, К.
Рассчитать энтальпию газов за топкой  значительно сложнее. Для этого необходимо определить температуру газов, покидающих топку h
значительно сложнее. Для этого необходимо определить температуру газов, покидающих топку h 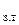 (
(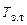 ). Зная h
). Зная h 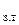 и коэффициент избытка воздуха
и коэффициент избытка воздуха 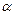 , по диаграмме I – h можно найти и
, по диаграмме I – h можно найти и  .
.
Температура h 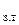 является результатом лучистого теплообмена между факелом и лучевоспринимающими поверхностями нагрева
является результатом лучистого теплообмена между факелом и лучевоспринимающими поверхностями нагрева 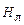 , расположенными в топке (поверхностями нагрева труб, обращенных в топку). Эффективность лучистого теплообмена определяется многими факторами, главные из которых – иалучательные свойства факела, поглощательные свойства стенок парообразующих труб, расположенных в топке, размеры факела и лучевоспринимающих поверхностей нагрева труб, обращенных в топку, средняя температура факела и стенок труб, воспринимающих теплоту в топке, и др.
, расположенными в топке (поверхностями нагрева труб, обращенных в топку). Эффективность лучистого теплообмена определяется многими факторами, главные из которых – иалучательные свойства факела, поглощательные свойства стенок парообразующих труб, расположенных в топке, размеры факела и лучевоспринимающих поверхностей нагрева труб, обращенных в топку, средняя температура факела и стенок труб, воспринимающих теплоту в топке, и др.
В лучистом теплообмене учет факторов, влияющих на теплообмен в топке, осуществляется совместно в безразмерном комплексе, называемом топочным критерием или критерием Больцмана Во, который равен
 , ,
| (3.24) |
| где | 
| – | константа излучения абсолютно черного тела, равная 5,67∙10–14 МВт/(м2∙К4); |
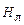
| – | лучевоспринимающая поверхность нагрева топки, м2; | |

| – | теоретическая температура в топке, К; | |

| – | средняя теплоемкость продуктов сгорания 1 кг топлива, МДж/(кг∙°С). |
Введем понятие безразмерной температуры за топкой h 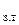 , причем h
, причем h 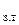 =
= 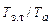 . На основании большого числа опытов по теплообмену, проведенных в топках судовых котлов, установлена следующая зависимость между безразмерной температурой за топкой h
. На основании большого числа опытов по теплообмену, проведенных в топках судовых котлов, установлена следующая зависимость между безразмерной температурой за топкой h 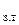 и критерием Больцмана Во
и критерием Больцмана Во
h  . .
| (3.25) |
Формула (3.25) является расчетной для определения h 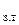 . Зная h
. Зная h 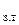 , найдем
, найдем 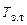 = h
= h 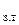
 и h
и h 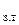 =
= 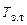 – 273, °С. По значениям h
– 273, °С. По значениям h 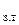 и коэффициента
и коэффициента 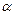 на диаграмме I –
на диаграмме I –  найдем
найдем  и затем по формуле (3.22) определим количество лучистой теплоты
и затем по формуле (3.22) определим количество лучистой теплоты  , переданной в топке поверхностям нагрева в единицу времени.
, переданной в топке поверхностям нагрева в единицу времени.
Для расчета h 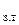 по формуле (3.25) надо подсчитать значение критерия Больцмана Во. Покажем последовательность расчета величин, входящих в уравнение (3.24).
по формуле (3.25) надо подсчитать значение критерия Больцмана Во. Покажем последовательность расчета величин, входящих в уравнение (3.24).
1. Коэффициент сохранения теплоты  определяется по формуле (3.21). Обычно
определяется по формуле (3.21). Обычно  = 0,5 ÷ 1,5%, откуда
= 0,5 ÷ 1,5%, откуда  = 0,995 ÷ 0,985.
= 0,995 ÷ 0,985.
2. Расход топлива В, кг/с, определяется из формулы (3.10) для главного котла или из формулы (3.11) для вспомогательного котла. Для последнего при условии, что он вырабатывает влажный пар в количестве 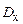 , кг/с, получим
, кг/с, получим
 , ,
| (3,26) |
| где | 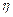 = 0,76 ÷ 0,92 = 0,76 ÷ 0,92
| – | для вспомогательных паровых котлов. |
Энтальпию влажного пара  определяют по формуле
определяют по формуле  , где
, где 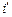 – энтальпия кипящей воды при давлении в котле, МДж/кг;
– энтальпия кипящей воды при давлении в котле, МДж/кг; 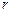 – скрытая теплота парообразования, МДж/кг (см. рис. 3.15);
– скрытая теплота парообразования, МДж/кг (см. рис. 3.15);  – массовое паросодержание (степень сухости) пара на выходе из пароводяного коллектора; обычно
– массовое паросодержание (степень сухости) пара на выходе из пароводяного коллектора; обычно  = 0,99 ÷ 0,995.
= 0,99 ÷ 0,995.
Энтальпию питательной воды  находят по формуле
находят по формуле  , где
, где  = 4190 Дж/кг;
= 4190 Дж/кг; 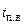 – температура питательной воды, °С.
– температура питательной воды, °С.
3. Средняя теплоемкость продуктов сгорания  , образующихся от сжигания 1 кг топлива в интервале температур от h
, образующихся от сжигания 1 кг топлива в интервале температур от h 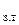 до h
до h 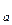 , равна, МДж/(кг∙°С),
, равна, МДж/(кг∙°С),
 . .
| (3.27) |
При использовании для расчетов формулы (3.27) величину h 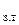 принимают равной h
принимают равной h 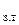 = h
= h 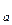 – (400 ÷ 600), °С.
– (400 ÷ 600), °С.
В конце расчета температуры h 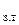 (h
(h 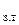 ) по формуле (3.25) полученное значение h
) по формуле (3.25) полученное значение h 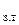 сопоставляется с предварительно принятым. При расхождении значений на ±50°С расчет повторяют, используя рассчитанное по формуле (3.25) значение h
сопоставляется с предварительно принятым. При расхождении значений на ±50°С расчет повторяют, используя рассчитанное по формуле (3.25) значение h 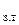 в качестве предварительного во втором приближении.
в качестве предварительного во втором приближении.
4. В паровых котлах с естественной циркуляцией и с горизонтальным расположением топочных устройств следует различать лучевоспринимающие поверхности экрана  и притопочного пучка
и притопочного пучка  .
.
Лучевоспринимающая поверхность сплошного бокового экрана, обращенного к топке, определяется как поверхность сплошной криволинейной стенки, проходящей через осевую линию ряда, то есть в виде произведения длины топки 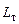 на длину освещенной части труб экрана
на длину освещенной части труб экрана  , измеренную по оси ряда
, измеренную по оси ряда
 . .
| (3.28) |
Если экранируется не только боковая стенка топки, но и фронтовые (одна или обе), то определяется лучевоспринимающая поверхность и этих фронтовых стен по формуле (3.28) с заменой величины 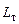 на ширину В.
на ширину В.
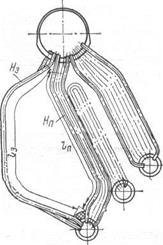 Рис. 3.5. Схема парового котла
(к определению лучевоспринимающей поверхности нагрева)
Рис. 3.5. Схема парового котла
(к определению лучевоспринимающей поверхности нагрева)
|
 Рис. 3.6. Паровой котел с естественной циркуляцией
(к определению расчетной конвективной поверхности нагрева):
1 – парообразующие; 2 – пароперегревательная; 3 – экономайзерная;
4 – воздухонагревательная
Рис. 3.6. Паровой котел с естественной циркуляцией
(к определению расчетной конвективной поверхности нагрева):
1 – парообразующие; 2 – пароперегревательная; 3 – экономайзерная;
4 – воздухонагревательная
|
Величину  определяют как произведение длины топки на среднюю освещенную длину труб притопочного пучка
определяют как произведение длины топки на среднюю освещенную длину труб притопочного пучка 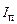 (Рис. 3.5), измеренную по оси второго ряда (освещается не вся длина второго ряда, так как концевые участки могут не освещаться),
(Рис. 3.5), измеренную по оси второго ряда (освещается не вся длина второго ряда, так как концевые участки могут не освещаться),
 . .
| (3.29) |
Согласно формуле (3.29), лучевоспринимающая поверхность притопочного пучка труб рассчитывается как поверхность сплошной изогнутой стенки, хотя на самом деле в пучке имеются зазоры между трубами. Тем не менее формула (3.29) справедлива и для пучка. Объясняется это тем, что лучи факела, прошедшие через зазоры между трубами первого ряда, будут восприняты трубами последующих рядов, а именно, вторым, третьим и т. д. рядом.
Суммарный эффект поглощения равноценен эффекту поглощения лучей криволинейной сплошной стенкой, имеющей те же размеры, 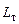 и
и 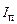 что и первые ряды пучка. Суммарная лучевос-принимающая поверхность труб в топке равна
что и первые ряды пучка. Суммарная лучевос-принимающая поверхность труб в топке равна
 . .
|
5. Метод определения теоретической температуры  (h
(h 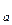 ) был рассмотрен ранее (см. стр. 42).
) был рассмотрен ранее (см. стр. 42).
Теплообмен в конвективных поверхностях нагрева. Конвективной поверхностью нагрева котла называется такая поверхность, теплообмен которой осуществляется в основном конвекцией, то есть соприкосновением при омывании поверхностей нагрева движущимся потоком (газом, паром, водой и др.). Конвективные поверхности нагрева (Рис. 3.6) выполняются в виде вертикальных пучков труб, например, пучки 1, 2 и 4, или в виде горизонтальных, например, пучок 3. Рабочее тело (вода, пар и др.) движется, как правило, внутри труб (продольное омывание), а продукты сгорания омывают эти трубы снаружи поперечным потоком (поперечное омывание).
Пусть энтальпия продуктов сгорания перед какой-либо конвективной поверхностью нагрева (то есть перед пучком труб) равна 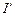 , а за пучком
, а за пучком  . Тогда количество конвективной теплоты, отданной в единицу времени продуктами сгорания при омывании трубного пучка, будет равно, МВт,
. Тогда количество конвективной теплоты, отданной в единицу времени продуктами сгорания при омывании трубного пучка, будет равно, МВт,
 . .
| (3.30) |
Это же количество теплоты должно быть воспринято рабочей средой (паром, водой), движущейся в трубах пучка с расходом D, кг/с, то есть
 , ,
| (3.31) |
| где |  и и 
| – | энтальпии рабочей среды при выходе из труб пучка и входе в трубы, МДж/кг. |
Уравнения (3.30) и (3.31) для конвективной поверхности называются балансовыми. Однако для теплового расчета конвективной поверхности нагрева их недостаточно, так как оказывается неизвестной площадь поверхности нагрева, необходимая для передачи теплоты  от газов к рабочей среде. Поэтому для расчета кроме уравнений (3.30) и (3.31) необходимо уравнение теплопередачи (теплообмена), МВт,
от газов к рабочей среде. Поэтому для расчета кроме уравнений (3.30) и (3.31) необходимо уравнение теплопередачи (теплообмена), МВт,
 , ,
| (3.32) |
| где | 
| – | коэффициент теплопередачи от газа к рабочему телу в трубах, Вт/(м2∙°С); |

| – | температурный напор или разность средних температур газа и рабочего тела в трубах, °С; | |

| – | расчетная площадь конвективной поверхности нагрева труб, м2. |
Множитель  в формулу (3.32) введен потому, что в ней размерность коэффициента теплопередачи выражается в Вт/(м2∙°С), тогда как для величины
в формулу (3.32) введен потому, что в ней размерность коэффициента теплопередачи выражается в Вт/(м2∙°С), тогда как для величины  на практике удобнее применять размерность в МВт.
на практике удобнее применять размерность в МВт.
Решив совместно уравнения (3.30) и (3.32), находят расчетную площадь конвективной поверхности нагрева  , м2,
, м2,
 , ,
| (3.33) |
под которой понимают полную площадь поверхности труб пучка, вычисляемую по наружному диаметру труб и расчетной длине и фактически равную, м2,
 , ,
| (3.34) |
| где | 
| – | наружный диаметр труб, м; |
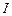
| – | средняя расчетная длина труб пучка, замеренная по оси среднего ряда от наружной кромки одного коллектора до наружной кромки другого (Рис. 3.6), м; | |

| – | число труб в ряду (поперек потока, шт.); | |

| – | число рядов труб в пучке (вдоль потока, шт.). |
Расчетную длину труб 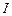 снимают с эскиза предварительно спроектированного конвективного пучка, в котором число рядов труб
снимают с эскиза предварительно спроектированного конвективного пучка, в котором число рядов труб  принимается. С эскиза снимают и ширину пучка, которая в данном случае равна длине котла
принимается. С эскиза снимают и ширину пучка, которая в данном случае равна длине котла 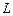 . Тогда число труб в ряду равно, шт.,
. Тогда число труб в ряду равно, шт.,
 , ,
| (3.35) |
| где | 
| – | поперечный шаг труб в пучке или расстояние между осями труб в ряду, м. |
Площадь поверхности нагрева одного ряда равна, м2,
 . .
|
Рассчитав  по уравнению (3.33) и определив
по уравнению (3.33) и определив  , находят требуемое из условия теплопередачи число рядов труб в пучке
, находят требуемое из условия теплопередачи число рядов труб в пучке 
 . .
| (3.36) |
В тепловом расчете конвективной поверхности нагрева важно уметь определять коэффициент теплопередачи  и температурный напор
и температурный напор  . Рассмотрим вывод формулы для определения коэффициента теплопередачи
. Рассмотрим вывод формулы для определения коэффициента теплопередачи  .
.
Пусть имеется металлическая стенка, омываемая снаружи горячими газами со средней температурой газов  . Изнутри стенка охлаждается за счет омывания ее нагреваемой средой (водой, паром) со средней температурой среды
. Изнутри стенка охлаждается за счет омывания ее нагреваемой средой (водой, паром) со средней температурой среды 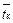 (Рис. 3.7). Толщина стенки равна
(Рис. 3.7). Толщина стенки равна 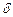 , м; коэффициент теплопроводности металла стенки
, м; коэффициент теплопроводности металла стенки  , Вт/(м∙°С); температура на наружной поверхности стенки
, Вт/(м∙°С); температура на наружной поверхности стенки 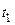 , на внутренней –
, на внутренней –  , °C.
, °C.
 Рис. 3.7. Схема передачи теплоты от продуктов сгорания через стенку трубы
к среде, движущейся в трубе (к выводу формулы для коэффициента
теплопередачи
Рис. 3.7. Схема передачи теплоты от продуктов сгорания через стенку трубы
к среде, движущейся в трубе (к выводу формулы для коэффициента
теплопередачи  ) )
|
В стационарном процессе передачи теплоты ее количество, отданное от греющей среды к стенке, прошедшее через стенку и отданное к нагреваемой среде, равны. По закону Ньютона количество теплоты, переданной от греющей среды, то есть от газов к наружной поверхности стенки площадью  (см. рис. 3.7), равно, МВт,
(см. рис. 3.7), равно, МВт,
 . .
| (3.37) |
По закону Фурье количество теплоты, прошедшей через металлическую стенку толщиной  , м, с площадью поверхности
, м, с площадью поверхности  , м2, равно, МВт,
, м2, равно, МВт,
 [ [  ] ]  . .
| (3.38) |
Количество теплоты, отданное от стенки к нагреваемой среде в трубах, будет равно, МВт,
 . .
| (3.39) |
В выражениях (3.37) и (3.39)  – коэффициент теплоотдачи от греющей среды к стенке и
– коэффициент теплоотдачи от греющей среды к стенке и  – коэффициент теплоотдачи от стенки к нагреваемой среде, Вт/(м2∙°С). Решив каждое из уравнений (3.37) – (3.39) относительно температурной разности и сложив левые и правые части полученных выражений, найдем
– коэффициент теплоотдачи от стенки к нагреваемой среде, Вт/(м2∙°С). Решив каждое из уравнений (3.37) – (3.39) относительно температурной разности и сложив левые и правые части полученных выражений, найдем
 . .
| (3.40) |
В общем случае стенка котельной трубки, через которую теплота передается от продуктов сгорания к нагреваемой среде (воде, пару) загрязнена снаружи слоем золы и сажи (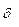 ,
,  ), а изнутри покрыта слоем накипи (
), а изнутри покрыта слоем накипи ( ,
,  ). Поэтому в формуле (3.40) появятся два новых члена, учитывающие это обстоятельство:
). Поэтому в формуле (3.40) появятся два новых члена, учитывающие это обстоятельство: 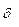 /
/  и
и  /
/  . Формула (3.40) примет вид
. Формула (3.40) примет вид
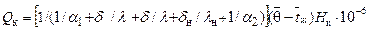 . .
| (3.41) |
Величины, стоящие в знаменателе  ,
, 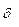 /
/  и т. д., называются термическими сопротивлениями.
и т. д., называются термическими сопротивлениями.
Введем следующие обозначения, Вт/(м2∙°С):
 , ,
| (3.42) |
 . .
| (3.43) |
Тогда формула (3.41) может быть записана в таком виде, МВт
 . .
|
В формуле для коэффициента теплопередачи (3.42) величины, находящиеся в знаменателе, имеют различные значения. В частности, величины  очень малы по сравнению с
очень малы по сравнению с  , поэтому ими можно пренебречь и получить для
, поэтому ими можно пренебречь и получить для  простую расчетную формулу, Вт/(м2∙°С),
простую расчетную формулу, Вт/(м2∙°С),
 , ,
| (3.44) |
| где | 
| – | коэффициент наружных загрязнений труб, м2∙°С/Вт. |
Формула (3.44) справедлива для определения  лишь в парообразующих и экономайзерных поверхностях нагрева.
лишь в парообразующих и экономайзерных поверхностях нагрева.
Для пароперегревателей и газовых воздухоподогревателей коэффициент теплопередачи  вычисляют по такой формуле, Вт/(м2∙°С)
вычисляют по такой формуле, Вт/(м2∙°С)
 . .
| (3.45) |
Коэффициент наружных загрязнений  , входящий в формулы (3.44) и (3.45), может иметь следующие значения: для главных паровых котлов
, входящий в формулы (3.44) и (3.45), может иметь следующие значения: для главных паровых котлов  = 0,003 ÷ 0,006 м2∙°С/Вт; для вспомогательных и утилизационных котлов
= 0,003 ÷ 0,006 м2∙°С/Вт; для вспомогательных и утилизационных котлов  = 0,003 ÷ 0,009 м2∙°С/Вт. Значение е следует принимать тем меньше, чем больше скорость газов.
= 0,003 ÷ 0,009 м2∙°С/Вт. Значение е следует принимать тем меньше, чем больше скорость газов.
Газы при омывании конвективных пучков отдают теплоту трубам не только конвекцией, но и излучением газов. Кроме того, поверхности нагрева омываются газовым потоком неравномерно. С учетом сказанного коэффициент теплоотдачи  от газов к трубам можно представить в виде, Вт/(м2∙°С),
от газов к трубам можно представить в виде, Вт/(м2∙°С),
 , ,
| (3.46) |
| где | 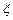
| – | коэффициент, учитывающий неравномерность омывания поверхности нагрева газовым потоком; |

| – | коэффициенты теплоотдачи соответственно конвекцией и излучением газов в межтрубном пространстве, Вт/(м2∙°С). |
Для вертикальных изогнутых пучков труб коэффициент неравномерности омывания 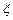 = 0,8 ÷ 0,9; для горизонтальных пакетов труб
= 0,8 ÷ 0,9; для горизонтальных пакетов труб 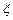 = 0,9 ÷ 0,95.
= 0,9 ÷ 0,95.
Коэффициент теплоотдачи излучением газа  в основном зависит от средней температуры газа в пучке и размеров излучающего межтрубного газового объема (газовой ячейки). Последняя величина очень мала, поэтому даже при высоких температурах газа значение
в основном зависит от средней температуры газа в пучке и размеров излучающего межтрубного газового объема (газовой ячейки). Последняя величина очень мала, поэтому даже при высоких температурах газа значение  невелико по сравнению с
невелико по сравнению с  . В парообразующих пучках, расположенных за топкой, можно принимать
. В парообразующих пучках, расположенных за топкой, можно принимать  = 8 ÷ 10 Вт/(м2∙°С); в пароперегревателях
= 8 ÷ 10 Вт/(м2∙°С); в пароперегревателях  = 5 ÷ 8 Вт/(м2-°С). В экономайзерах и воздухоподогревателях из-за низкой температуры газа
= 5 ÷ 8 Вт/(м2-°С). В экономайзерах и воздухоподогревателях из-за низкой температуры газа  ≈ 0.
≈ 0.
Формулы для определения коэффициента теплоотдачи конвекцией  являются эмпирическими. Для их получения проводят опыты по теплоотдаче, а результаты обрабатывают на основе теории подобия. Расчетные формулы для определения
являются эмпирическими. Для их получения проводят опыты по теплоотдаче, а результаты обрабатывают на основе теории подобия. Расчетные формулы для определения  выведены для двух случаев: 1) при поперечном омывании пучка труб потоком; 2) при продольном омывании. Кроме того, различают поперечное омывание пучков с коридорным и шахматным расположением труб.
выведены для двух случаев: 1) при поперечном омывании пучка труб потоком; 2) при продольном омывании. Кроме того, различают поперечное омывание пучков с коридорным и шахматным расположением труб.

|  Ряды труб, z 2
Ряды труб, z 2
|
| Рис. 3.8. Схема компоновки пучков труб при поперечном омывании: а – коридорное строение; б – шахматное строение; 1, 2, 3 – номера рядов |
При поперечном омывании коридорных гладкотрубных пучков труб (Рис. 3.8, а) коэффициент теплоотдачи конвекцией определяют по формуле, Вт/(м2∙°С),
 , ,
| (3.47) |
| где | 
| – | коэффициент теплопроводности среды (газа, воздуха), омывающей трубы, Вт/(м∙°С); |

| – | наружный диаметр труб, м; | |

| – | скорость среды, м/с; | |

| – | коэффициент кинематической вязкости среды, м2/с; | |

| – | число Прандтля среды; | |

| – | поправка на число рядов труб  ; ;
| |

| – | поправка на компоновку, зависящая от относительного поперечного  и продольного и продольного  шагов. шагов.
|
Поправки  и
и  находят следующим образом:
находят следующим образом:
 ; ;
 . .
| } | (3.48) |
 ; ;
 . .
| } | (3.49) |
При поперечном омывании шахматных гладкотрубных пучков (см. рис. 3.8, б) газами или воздухом коэффициент  вычисляют по формуле, Вт/(м2∙°С),
вычисляют по формуле, Вт/(м2∙°С),
 . .
| (3.50) |
В этом случае поправка  определяется так:
определяется так:
 ; ;
 . .
| } | (3.51) |
Поправка на компоновку  , зависящая от
, зависящая от  и параметра
и параметра  , где
, где  – относительный диагональный шаг, определяется так:
– относительный диагональный шаг, определяется так:
 ; ;
 . .
| } | (3.52) |
Остальные обозначения здесь те же, что и в формуле (3.47).
При продольном омывании поверхности нагрева движущейся средой, например, потоком газа, воздуха, пара или воды  равен, Вт/(м2∙°С),
равен, Вт/(м2∙°С),
 Рис. 3.9. График зависимости величин
Рис. 3.9. График зависимости величин  для газа
от средней температуры газа в пучке для газа
от средней температуры газа в пучке 
|
 , ,
| (3.53) |
| где | 
| – | эквивалентный диаметр, м. При движении среды внутри труб он равен внутреннему диаметру. |
Параметры  для газов находят из графика, представленного на рис. 3.9.
для газов находят из графика, представленного на рис. 3.9.
При движении среды в каналах некруглого сечения и продольном омывании пучков труб
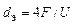 , ,
| (3.54) |
| где | 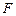
| – | площадь сечения канала для прохода среды, м2; |

| – | полный смоченный периметр канала, м. |
Поправка  учитывает влияние температурного фактора и зависит от средней температуры среды
учитывает влияние температурного фактора и зависит от средней температуры среды  и температуры стенки
и температуры стенки  , К. При охлаждении газов и нагревании пара
, К. При охлаждении газов и нагревании пара  = 1,0. Поправка
= 1,0. Поправка  на относительную длину канала учитывается только при
на относительную длину канала учитывается только при  . Если отношение
. Если отношение  равно 10; 20; 30 и 40, то
равно 10; 20; 30 и 40, то  соответственно равна 1,4; 1,14; 1,05 и 1,02.
соответственно равна 1,4; 1,14; 1,05 и 1,02.
Значения  для кипящей воды и насыщенного пара даны в зависимости от температуры насыщения
для кипящей воды и насыщенного пара даны в зависимости от температуры насыщения  или от средней температуры и давления – для некипящей воды и перегреваемого пара.
или от средней температуры и давления – для некипящей воды и перегреваемого пара.
Скорость газа до при омывании пучков труб определяется по формуле, м/с,
 , ,
| (3.55) |
| где | 
| – | объем газа от сжигания 1 кг топлива, определяемый по формуле (2.25), м3/кг; |

| – | средняя температура газа в пучке, °С. |
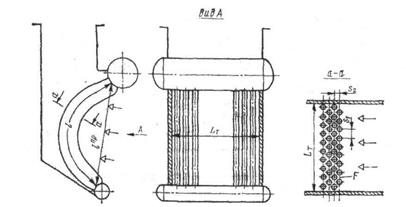 Рис. 3.10. Схема парообразующего пучка парового котла
с естественной циркуляцией (к определению площади живого сечения)
Рис. 3.10. Схема парообразующего пучка парового котла
с естественной циркуляцией (к определению площади живого сечения)
|
Величина 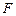 рассчитывается по формуле: (Рис. 3.10), м2,
рассчитывается по формуле: (Рис. 3.10), м2,
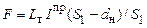 , ,
| (3.56) |
| где | 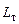
| – | ширина пучка труб (длина топки), м; |

| – | длина проекции пучка на плоскость, перпендикулярную направлению потока, м. |
Скорость движения воздуха в воздухоподогревателе равна, м/с,
 . .
| (3.57) |
Здесь  .
.
Скорость пара или воды, движущейся в трубах, вычисляется по формуле, м/с,
 , ,
| (3.58) |
| где |  , , 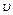
| – | расход, кг/с, и средний удельный объем пара или воды, м3/кг; |

| – | площадь живого сечения труб, м2. |
Температурным напором называется усредненная по всей поверхности нагрева разность температур греющей и нагреваемой сред. Температурный напор зависит от начальных и конечных зна-
чений температуры сред и направления их движения относительно друг друга.
Различают три направления движения сред: прямоток (Рис. 3.11, а), противоток (Рис. 3.11, б) и перекрестный ток (Рис. 3.12).
 Рис. 3.11. Схемы взаимного направления движения сред
(к определению температурного напора)
Рис. 3.11. Схемы взаимного направления движения сред
(к определению температурного напора)
|
 Рис. 3.12. Схемы перекрестного тока:
1 – однократного; 2 – двухкратного; 3 – трехкратного; 4 – четырехкратного
Рис. 3.12. Схемы перекрестного тока:
1 – однократного; 2 – двухкратного; 3 – трехкратного; 4 – четырехкратного
|
С теплотехнической точки зрения противоток обладает наибольшей эффективностью. Применение противотока позволяет повысить температурный напор. Перекрестный ток с числом ходов  относится к противотоку либо к прямотоку в зависимости от направления взаимного движения сред.
относится к противотоку либо к прямотоку в зависимости от направления взаимного движения сред.
 Рис. 3.13. Номограмма для определения коэффициента
Рис. 3.13. Номограмма для определения коэффициента  , входящего
в формулу температурного напора при перекрестном токе , входящего
в формулу температурного напора при перекрестном токе
|
Для прямотока, противотока и многократного перекрестного тока (при  ) средний температурный напор
) средний температурный напор  рассчитывается по формуле
рассчитывается по формуле
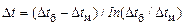 , ,
| (3.59) |
| где | 
| – | разность температур обеих жидкостей на том конце поверхности нагрева Н, на котором она наибольшая (например,  при прямотоке), °С; при прямотоке), °С;
|

| – | разность температур обеих жидкостей на том конце поверхности нагрева, где она наименьшая (например,  при прямотоке), °С. при прямотоке), °С.
|
Если выполняется условие  , то можно пользоваться простой формулой
, то можно пользоваться простой формулой
 . .
| (3.60) |
Формулы (3.59) и (3.60) справедливы и в случае, когда температура одной из жидкостей изменяется, а температура другой остается постоянной (Рис. 3.11, в). Это имеет место в парообразующей поверхности нагрева, для которой формула (3.12) получает вид
 , ,
| (3.61) |
где  – температура насыщения, °С.
– температура насыщения, °С.
Для перекрестного тока при  , а также для смешанного тока температурный напор определяют по формуле
, а также для смешанного тока температурный напор определяют по формуле
 , ,
| (3.62) |
| где | 
| – | поправочный коэффициент ( < 1); < 1);
|

| – | температурный напор, подсчитанный для схемы противотока, °С. |
При однократном и многократном перекрестном токе, если взаимное направление потоков соответствует противоточной схеме движения (см. рис. 3.12), коэффициент  определяют по номограмме, представленной на рис. 3.13, где кривые 1, 2, 3 и 4 (в нижней части рисунка) относят к соответствующим схемам рис. 3.12.
определяют по номограмме, представленной на рис. 3.13, где кривые 1, 2, 3 и 4 (в нижней части рисунка) относят к соответствующим схемам рис. 3.12.
Не нашли, что искали? Воспользуйтесь поиском: