Характеристики модели СМО с ожиданием и приоритетами

Среднее время ожидания ячейки k-приоритета в системе M/D/1/ ∞ с

приоритетным обслуживанием равно

, (4.4)

где: - интенсивность поступлений ячеек i-приоритета, первый приоритет – наивысший,

где Bi - нагрузка потока i – приоритета, бит/с

L – длина ячейки, бит

n – число приоритетов,

,

- коэффициент использования линии ячейками i-приоритета,

μ_i- интенсивность обслуживания ячеек i-приоритета.

,

где C_ATM - пропускная способность канала, доступная уровню АТМ.

При n=2 получим

, (4.5)

Среднее время ожидания пакета k-приоритета в системе M/G/1/ ∞ с

приоритетным обслуживанием равно

, (4.6)

где λ_i- интенсивность поступлений пакетов i-приоритета, первый приоритет –

наивысший,

n – число приоритетов,

- второй момент длительности обслуживания пакетов i-приоритета.

- второй момент длительности передачи пакета,

- первый момент длительности передачи пакета,

σ² - дисперсия длительности передачи пакета.

Для потоков с экспоненциально распределенной длиной пакета

Для потоков с детерминированной длиной пакета

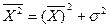
Дисперсия времени ожидания пакета в очереди в системе M/G/1/ ∞ с

приоритетным обслуживанием равна

, (4.7)

- первый момент времени ожидания (средняя задержка ожидания) в

очереди ячейки k-приоритета,

- второй момент времени ожидания в очереди ячейки k-приоритета,

K= 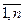, n - число приоритетов.

, (4.8)

где ,

- третий момент длительности передачи пакета.

Для экспоненциального закона длины пакета

Для детерминированных длин пакетов

Не нашли, что искали? Воспользуйтесь поиском: