Решение вопроса о Солнечной системе

Независимо от того, была научная революция революцией или нет, но началась она с Коперника. Николай Коперник родился в 1473 г. в Польше в прусской семье, предыдущее поколение которой эмигрировало из Силезии. В возрасте десяти лет Николай потерял отца, но, к счастью, его поддерживал дядя, который разбогател, служа в церкви, и несколько лет спустя стал епископом Вармии (Эрмланд) в северо-восточной Польше. Закончив университет в Кракове, где он, возможно, прослушал курс астрономии, Коперник в 1496 г. стал студентом канонического права в университете Болоньи и начал вести астрономические наблюдения как помощник астронома Доменико Мария Наваро, который был учеником Региомонтана. В Болонье Коперник узнал, что при участии своего дяди он был утвержден в качестве одного из шестнадцати каноников кафедрального епископства во Фромборке в Вармии. С этого поста он до конца жизни получал хороший доход, исполняя весьма необременительные церковные обязанности. Коперник так и не стал священником. Изучив азы медицины в университете Падуи, в 1503 г. Коперник получил степень доктора юриспруденции в университете Феррары и вскоре вернулся в Польшу. В 1510 г. он поселился во Фромборке, построил небольшую обсерваторию и прожил в городе до самой своей смерти в 1543 г.

После своего возвращения во Фромборк Коперник анонимно написал небольшую работу, позже получившую наименование «Малый комментарий о гипотезах, относящихся к небесным движениям» (De hypothesibus motuum coelestium a se constitutis commentariolus), которую часто называют «Комментарий» или «Малый комментарий»[187]. «Комментарий» был опубликован только после смерти автора и не оказал особого влияния на развитие науки, в отличие от его дальнейших сочинений, но дает хорошее представление об идеях, которые в будущем оказывали влияние на работу Коперника.

В «Комментарии» после краткого критического обзора более ранних теорий движения планет Коперник заявляет семь принципов своей новой теории. Далее я привожу цитаты с некоторыми комментариями:

1. «Не существует одного центра для всех небесных орбит или сфер»[188]. (Среди историков есть разногласие по поводу того, считал ли Коперник эти тела заключенными в материальные сферы, как полагал Аристотель.)

2. «Центр Земли не является центром мира, но только центром тяготения и центром лунной орбиты».

3. «Все сферы движутся вокруг Солнца, расположенного как бы в середине всего, так что около Солнца находится центр мира». (Но, как мы будем говорить далее, Коперник сделал центром орбит Земли и других планет не само Солнце, а точку рядом с Солнцем.)

4. «Отношение, которое расстояние между Солнцем и Землей имеет к высоте небесной тверди, меньше отношения радиуса Земли к ее расстоянию от Солнца, так что по сравнению с высотой тверди оно будет даже неощутимым». (Вероятно, Коперник сделал это допущение, чтобы объяснить, почему мы не наблюдаем годичный параллакс – видимое годовое движение звезд, вызванное обращением Земли вокруг Солнца. Но проблема параллакса в «Комментарии» нигде не упоминается.)

5. «Все движения, замечающиеся у небесной тверди, принадлежат не ей самой, но Земле. Именно Земля с ближайшими к ней стихиями вся вращается в суточном движении вокруг неизменных своих полюсов, причем твердь и самое высшее небо остаются все время неподвижными».

6. «Все замечаемые нами у Солнца движения не свойственны ему, но принадлежат Земле и нашей сфере, вместе с которой мы вращаемся вокруг Солнца, как и всякая другая планета; таким образом, Земля имеет несколько движений».

7. «Кажущиеся прямые и попятные движения планет принадлежат не им, но Земле. Таким образом, одно это ее движение достаточно для объяснения большого числа видимых в небе неравномерностей».

В «Комментарии» Коперник не мог заявить, что его схема лучше соответствует наблюдениям, чем система Птолемея. Во-первых, это было не так. В самом деле, как это могло быть, когда по большей части Коперник строил свою теорию на информации, полученной из «Альмагеста» Птолемея, а не на своих собственных наблюдениях?[189]Вместо того чтобы заняться новыми наблюдениями, на которые он мог бы сослаться, Коперник выделил ряд эстетических преимуществ своей теории.

Одним из преимуществ было то, что движение Земли объясняло множество видимых перемещений Солнца, звезд и планет. Таким образом Коперник избавился от подгонки, предполагаемой в теории Птолемея, согласно которой центр эпициклов Меркурия и Венеры всегда должен был находиться на линии между Землей и Солнцем, а линии между Марсом, Юпитером и Сатурном и соответственно центры их эпициклов должны были всегда оставаться параллельными линии между Землей и Солнцем. Вследствие этого движение центра эпицикла каждой внутренней планеты вокруг Земли и, в свою очередь, обращение каждой внешней планеты по своему эпициклу должно было подгоняться так, чтобы завершаться точно за один год. Коперник увидел, что все эти неестественные требования просто отражают тот факт, что мы смотрим на Солнечную систему с площадки, обращающейся вокруг Солнца.

Другим эстетическим преимуществом теории Коперника должна была быть большая точность, касающаяся размеров орбит планет. Вспомним, что видимое движение планет в астрономии Птолемея зависело не от значений их эпициклов и деферентов, а только от соотношения радиусов эпицикла и деферента для каждой планеты. Если хочется, то можно взять деферент для Меркурия больше, чем деферент для Сатурна, главное – подобрать правильное значение эпицикла для Меркурия. Вслед за Птолемеем в «Планетных гипотезах» стало традиционным определять размеры орбит, опираясь на предположение, что максимальное расстояние от одной планеты до Земли равно минимальному расстоянию от Земли до следующей в порядке счета вовне планеты. Это закрепляло относительные размеры орбит для любого выбранного порядка планет, идущих от Земли, но выбор можно было делать весьма произвольно. В любом случае предположение, сделанное Птолемеем в «Планетных гипотезах», не было основано на наблюдениях и не подтверждалось ими.

Напротив, для того, чтобы согласовать схему Коперника с наблюдениями, радиус орбиты для каждой планеты должен был иметь определенное соотношение с радиусом орбиты Земли[190].

Точнее говоря, из-за того, что Птолемей по-разному представил эпициклы для внутренних и внешних планет (не будем говорить о последующих усложнениях, связанных с эллиптической формой орбиты), отношение между радиусами эпициклов и деферентов должно равняться отношению между расстояниями от Солнца до Земли и до планеты для внутренних планет и тому же отношению, но обратному – для внешних планет (см. техническое замечание 13). Коперник представил результаты другим способом, в виде сложной «схемы триангуляции», которая создавала ложное впечатление, что он разработал новую модель для предсказаний движения небесных тел, которую подтверждали наблюдения. Однако Коперник действительно нашел правильные радиусы орбит планет. Он открыл, что по отношению к Солнцу планеты расположены в следующем порядке: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн. Это точно совпадает с периодами их обращения, которые Коперник оценил соответственно в три месяца, девять месяцев, год, два с половиной года, двенадцать лет и тридцать лет. Хотя еще не существовало теории, объясняющей скорость движения планет по их орбитам, должно быть, Коперник понял космическую закономерность: чем больше орбита планеты, тем медленнее она обращается вокруг Солнца[191].

Схема Коперника является классическим примером того, как теория может быть выбрана по эстетическим критериям, без всякого экспериментального доказательства, которое могло бы дать ей преимущество перед другими теориями. В случае с теорией Коперника, изложенной в «Комментарии», достоинство ее было в том, что очень многие характерные особенности теории Птолемея объяснялись одним махом с помощью вращения Земли и ее обращения вокруг Солнца, а также теория Коперника по сравнению с теорией Птолемея правильно утверждала порядок планет и размер их орбит. Коперник признавал, что идея вращения Земли была предложена очень давно, еще пифагорейцами, но также (совершенно справедливо!) отметил, что они «необоснованно отстаивали» ее, не приводя никаких аргументов, которые он мог бы развить.

В теории Птолемея, кроме подгонки и неуверенности по поводу размеров и порядка расположения планет, было кое-что еще, что не нравилось Копернику. Согласившись с указаниями Платона о том, что планеты должны двигаться с постоянной скоростью по круговым орбитам, Коперник отказался от используемых Птолемеем понятий типа экванта, которые нужны были для объяснения реально существующих отклонений от кругового движения с постоянной скоростью. Как это уже делал аш-Шатир, Коперник увеличил количество эпициклов: шесть для Меркурия, три для Луны и по четыре для Венеры, Марса, Юпитера и Сатурна. Здесь он не добился никаких улучшений по сравнению с «Альмагестом».

Эта работа Коперника является иллюстрацией того, что неоднократно повторялось в истории физики, когда простая и красивая теория, которая достаточно хорошо согласуется с наблюдением, оказывается ближе к истине, чем теория, которая лучше нее согласуется с наблюдением, но ужасно сложна. Самую простую версию идей Коперника в общем можно свести к тому, что все планеты, в том числе и Земля, обращаются по круговым орбитам с постоянной скоростью вокруг Солнца, которое находится точно в центре этих орбит, и нигде нет никаких эпициклов. Эта теория согласуется с простейшей версией астрономической теории Птолемея, в которой для каждой планеты существует только один эпицикл, у Солнца и Луны эпициклов нет, а также нет никаких эксцентров и эквантов. Эти теории не очень точно согласуются с наблюдением, поскольку планеты обращаются не по круговым орбитам, а по почти круглым эллиптическим, их скорость только приблизительно постоянная, а Солнце находится не в центре их орбит, а в точке, которая слегка смещена от центра и называется фокусом (см. техническое замечание 18). Коперник мог бы пойти еще дальше, введя по примеру Птолемея эксцентр и эквант для орбиты каждой планеты, включая Землю. Тогда отличие наблюдений от теоретических предсказаний стало бы столь мало, что не могло быть измерено астрономами того времени.

В развитии квантовой механики есть эпизод, который показывает, что не надо слишком заострять внимание на небольших расхождениях с наблюдениями. В 1925 г. Эрвин Шрёдингер разработал метод расчета энергий состояний простейшего атома – водорода. Его результаты хорошо согласовывались с общей картиной этих энергий, но в тонких деталях, где он стремился учесть расхождения между Специальной теорией относительности и классической механикой Ньютона, они не совпадали с точными результатами измерений. Шрёдингер некоторое время скрывал свои результаты, но потом мудро рассудил, что получить грубую схему уровней энергии – это уже значительное достижение, вполне достойное публикации, а точный учет релятивистских эффектов может подождать (его сделал несколько лет спустя Поль Дирак).

Вдобавок к многочисленным эпициклам Коперник добавил еще одно усложнение, очень похожее на эксцентр в астрономии Птолемея. Центром земной орбиты было взято не Солнце, а некая точка на относительно небольшом расстоянии от Солнца. Эти усложнения были нужны для того, чтобы попытаться объяснить разные явления, такие как неравенство в длительности времен года, открытое Евктемоном. Эти явления действительно связаны с тем, что Солнце находится в фокусе, а не в центре эллиптической орбиты Земли, и скорость движения Земли по орбите не является постоянной.

Другое усложнение Коперник ввел только из-за неверно понятого явления. Кажется, он считал, что обращение Земли вокруг Солнца дает поворот земной оси на 360° в год вокруг направления, перпендикулярного к плоскости орбиты Земли, – так же как палец на вытянутой руке танцора, выполняющего пируэт, каждый раз за один его оборот поворачивается на 360° вокруг вертикали (возможно, здесь на Коперника оказала влияние древняя идея о том, что планеты двигаются, прикрепленные к твердым прозрачным сферам). Конечно, направление земной оси в течение года ощутимо не меняется, поэтому Копернику пришлось придать Земле еще один, третий вид движения вдобавок к ее обращению вокруг Солнца и вращению вокруг своей оси. Оно должно было компенсировать эффект от мнимого разворота земной оси. Коперник предполагал, что эта взаимная компенсация не должна быть идеальной, так как земная ось поворачивается в течение очень многих лет, что дает медленную прецессию равноденствий, которая была открыта Гиппархом. После появления работ Ньютона стало ясно, что на самом деле обращение Земли вокруг Солнца не оказывает никакого влияния на направление земной оси, если не считать слабых эффектов, связанных с действием силы тяготения Солнца и Луны на экваториальное расширение Земли. Таким образом, как доказал Кеплер, никакая предложенная Коперником взаимная компенсация этих движений не была нужна.

Но даже со всеми этими усложнениями теория Коперника все равно была несколько проще теории Птолемея, но кардинально не отличалась. Хотя сам ученый этого не понимал, теория Коперника была бы намного ближе к реальной картине, если бы он не озаботился эпициклами, а оставил в своей теории маленькие неточности, с которыми справились бы в будущем.

В «Комментарии» содержится не слишком много технических деталей. Их гораздо больше в главном труде Коперника «О вращении небесных сфер»[192], который обычно называют «О вращении». Этот труд был закончен в 1543 г., когда ученый уже был при смерти. Книга начинается с посвящения Алессандру Фарнезе, папе римскому Павлу III. В нем Коперник напоминает о старом споре между теорией гомоцентрических сфер Аристотеля и теорией эксцентров и эпициклов Птолемея, указывая, что первая не опирается на наблюдения, а вторая «противоречит основным принципам равномерности движения». В поддержку своей дерзкой идеи о вращении Земли Коперник цитирует высказывание Плутарха:

«Другие считают Землю неподвижной, но пифагореец Филолай считал, что она обращается около центрального огня по косому кругу совершенно так же, как Солнце и Луна. Гераклид Понтийский и пифагореец Экфант тоже заставляют Землю двигаться, но не поступательно, а как бы привязанной вроде колеса, с запада на восток вокруг собственного ее центра».

В стандартном издании «О вращении» Коперник не упоминает Аристарха, но его имя появлялось в рукописи, а потом было вычеркнуто. Далее Коперник объясняет, что, поскольку другие ученые размышляли о движении Земли, то ему тоже необходимо позволить проверить эту идею. Затем он описывает свое заключение:

«Предположив существование тех движений, которые, как будет показано ниже в самом произведении, приписаны мною Земле, я, наконец, после многочисленных и продолжительных наблюдений обнаружил, что если с круговым движением Земли сравнить движения и остальных блуждающих светил и вычислить эти движения для периода обращения каждого светила, то получатся наблюдаемые у этих светил явления. Кроме того, последовательность и величины светил, все сферы и даже само небо окажутся так связанными, что ничего нельзя будет переставить ни в какой части, не произведя путаницы ни в каких частях и в самой Вселенной».

Как и в «Комментарии», Коперник ссылался на тот факт, что его теория лучше предсказывала явления, чем теория Птолемея; она определяла уникальный порядок планет и размеры их орбит, которые совпадали с наблюдением, тогда как теория Птолемея оставляла эти вопросы нерешенными. Конечно, у Коперника не было никаких способов, чтобы подтвердить правильность радиусов орбит, не приняв свою теорию за истину. Эту задачу решил Галилей, наблюдая за фазами планет.

Труд Коперника «О вращении» полон технических деталей. В нем автор развивает общие идеи, заявленные в «Комментарии». Особого упоминания достоин тот факт, что Коперник в Книге 1 априорно постулирует положение о том, что любое движение планет должно являться комбинацией круговых движений. Так, Книга 1 начинается словами:

«Прежде всего, мы должны заметить, что мир является шарообразным или потому, что эта форма совершеннейшая из всех и не нуждается ни в каких скрепах и вся представляет цельность [здесь Коперник очень напоминает Платона], или потому, что эта форма среди всех других обладает наибольшей вместимостью, что более всего приличествует тому, что должно охватить и сохранить все [так и есть – максимальный объем имеют шарообразные тела]; или же потому, что такую форму, как мы замечаем, имеют и самостоятельные части мира, именно Солнце, Луна и звезды [как он мог судить о форме звезд?]; или потому, что такой формой стремятся ограничить себя все предметы, как можно видеть у водяных капель и других жидких тел, когда они хотят быть ограниченными своей свободной поверхностью [это эффект поверхностного натяжения, который не имеет никакого отношения к форме планет]. Поэтому никто и не усомнится, что такая форма придана и божественным телам».

Коперник продолжает объяснения в главе 4, где пишет, что вследствие вышеизложенного движение небесных тел является «равномерным, вечным и круговым или составленным из нескольких круговых».

Далее в Книге 1 Коперник указывает на одну из самых красивых сторон гелиоцентрической системы, которая показывает, почему Меркурий и Венера никогда не видны на небе далеко от Солнца. Например, тот факт, что Венеру никогда не видно далее чем примерно в 45° от Солнца, объясняется тем, что размер орбиты Венеры составляет около 70 % орбиты Земли (см. техническое замечание 19). Как мы уже видели в главе 11, в теории Птолемея для объяснения этого факта требовалось подогнать движение Меркурия и Венеры так, чтобы центры эпициклов всегда находились на линии между Землей и Солнцем. Система Коперника делает ненужной и птолемеевскую подгонку движения внешних планет, которая требовала, чтобы линия между планетой и центром ее эпицикла была параллельна линии между Землей и Солнцем.

Система Коперника была встречена протестами со стороны религиозных деятелей, которые начали возмущаться еще до публикации трактата «О вращении». Этот конфликт отражен в знаменитой дискуссии XIX в. «Борьба религии с наукой»[193], написанной первым президентом Корнелльского университета Эндрю Диксоном Уайтом, который приписывает ряд недостоверных высказываний Лютеру, Меланхтону, Кальвину и Уэсли. Но такой конфликт существовал на самом деле. Сохранилась запись бесед Мартина Лютера с его учениками в Виттенберге, которая называется «Застольные беседы»[194](Tischreden). Запись от 4 июня 1539 г. гласит:

«Упоминался один новый астролог, который хотел доказать, что вращается Земля, а не небеса, Солнце и Земля… [Лютер отмечает] «Что поделаешь. Тот, кто хочет быть умным, не должен соглашаться ни с чем, что ценят другие. Он должен добиваться всего сам. Так делает дурак, который желает перевернуть всю астрономию с ног на голову. Даже если все старые убеждения будут смяты и отброшены, я буду верить в Священное Писание. Ибо Иисус [Навин] остановил Солнце, а не Землю»[195].

Через несколько лет после публикации трактата «О вращении» коллега Лютера Филипп Меланхтон (1497–1560) присоединился к нападкам на Коперника, теперь цитируя Екклезиаст 1:5: «Восходит солнце, и заходит солнце, и спешит к месту своему, где оно восходит».

Противоречия с тем, что говорилось в Библии, естественно, составляли серьезную проблему для протестантов, которые заменили авторитет папы Святым Писанием. Кроме того, новая теория являлась потенциальной проблемой для всех религий: ведь дом человечества, Земля, оказалась всего лишь еще одной планетой в ряду из пяти других.

Возникли даже сложности с публикацией «О вращении». Коперник послал свою рукопись издателю в Нюрнберг. Издатель пригласил в качестве редактора лютеранского священника Андреаса Озиандера, который увлекался астрономией. Возможно, пытаясь выразить свои собственные взгляды, Озиандер добавил предисловие, которое считали написанным Коперником до тех пор, пока век спустя подмена не была раскрыта Кеплером. В этом предисловии Озиандер «заставил» Коперника отказаться от намерения раскрыть истинную природу орбит планет[196]:

«Ибо это обязанность астронома – сопоставить историю [видимого] небесного движения через внимательное и грамотное изучение. Затем он должен постичь и продумать случаи этого движения или гипотезы по поводу их. Поскольку в любом случае он не может понять реальное положение дел, он будет принимать любые предположения, которые могут верно рассчитать движение тел, исходя из принципов геометрии как в прошлом, так и в будущем».

Предисловие Озиандера заканчивалось следующими словами:

«Поскольку рассматриваются только гипотезы, никто не ожидает, что что-то будет с полной определенностью сказано об астрономии, которая не обеспечивает такой определенности, во избежание того, чтобы не принять за истину идеи, измысленные с другой целью, и отделить от знания большую глупость, когда наткнется на нее».

Это напоминает рассуждения Гемина, жившего примерно в 70 г. до н. э. (я цитировал его в главе 8), но эти слова противоречат явному намерению Коперника – описать в «Комментарии» и в «О вращении» реальное состояние того, что теперь называется Солнечной системой.

Несмотря на мнение некоторых церковных лидеров по поводу гелиоцентрической теории, в общем протестантская церковь не совершала попыток запретить труды Коперника. До начала XVII в. не было возражений и у католиков. Знаменитая казнь Джордано Бруно в 1600 г. римской инквизицией произошла не из-за того, что он поддерживал Коперника, а из-за его еретических измышлений, в которых (по стандартам того времени) он был, разумеется, виновен. Но, как мы увидим далее, в XVII в. католическая церковь начала очень серьезное преследование идей Коперника.

Для будущего науки было очень важно принятие мыслей Коперника его коллегами-астрономами. Первым, кого Коперник сумел убедить, был его единственный ученик Георг Иоахим Ретик, который в 1540 г. опубликовал изложение теории Коперника, а в 1543 г. передал трактат «О вращении» в руки нюрнбергского издателя. Первоначально Ретик собирался написать предисловие к «О вращении», но когда он вынужден был уехать, чтобы получить место в Лейпциге, эта задача, к сожалению, досталась Озиандеру. Ранее Ретик помогал Меланхтону сделать Виттенбергский университет центром изучения математики и астрономии.

В 1551 г. теория Коперника завоевала престиж благодаря тому, что под покровительством Альбрехта, герцога Прусского, ее использовал Эразм Рейнгольд при составлении новых астрономических таблиц. Созданные им «Прусские таблицы» позволяли вычислять положение планет в зодиаке в любой произвольно взятый день. Таблицы эти были значительно улучшены по сравнению с существовавшими до того «Альфонсовыми таблицами», созданными в Кастилии в 1275 г. при дворе короля Альфонсо Х. На самом деле улучшения были связаны не с превосходством теории Коперника, а с тем, что за столетия (с 1275 по 1551 г.) было накоплено множество результатов наблюдений, а также, возможно, с тем, что простота гелиоцентрической системы делала расчеты проще. Конечно, приверженцы концепции о неподвижной Земле могли возразить, что основная идея трактата «О вращении» просто обеспечивает удобную схему для расчетов, а не отражает реальную картину мира. В самом деле, «Прусские таблицы» использовались астрономом и математиком, иезуитом Христофором Клавием при проведении реформы календаря в 1582 г. во время правления папы Григория XIII. Эта реформа дала нам современный григорианский календарь, но Клавий так и не отказался от своей веры в неподвижность Земли.

Один математик пытался примирить эту веру с теорией Коперника. В 1568 г. Каспар Пейцер, зять Меланхтона и профессор математики в Виттенбергском университете, в своем труде «Гипотезы о небесных сферах» (Hypotyposes orbium coelestium) писал, что с помощью математической трансформации возможно переписать теорию Коперника так, что Земля, а не Солнце, окажется неподвижной. Именно этого результата удалось позже достигнуть одному из учеников Пейцера – Тихо Браге.

Тихо Браге был лучшим астрономом-наблюдателем до изобретения телескопа и автором самой правдоподобной системы мира, альтернативной теории Коперника. Он родился в 1546 г. в провинции Сконе, которая находится в южной части Швеции, но в те времена принадлежала Дании. Тихо был сыном датского дворянина. Он учился в университете Копенгагена, где в 1560 г. на него произвело большое впечатление успешное предсказание частного солнечного затмения. Браге учился в нескольких университетах Германии и Швейцарии: в Лейпциге, Виттенберге, Ростоке, Базеле и Аугсбурге. За эти годы он изучил «Прусские таблицы», и его ошеломил тот факт, что эти таблицы успешно предсказали дату сближения Юпитера и Сатурна в 1563 г. с точностью до нескольких дней, тогда как старые «Альфонсовы таблицы» ошиблись на несколько месяцев.

Вернувшись в Данию, Браге некоторое время жил в доме своего дяди в Херреваде в Сконе. Там в 1572 г. он наблюдал в созвездии Кассиопеи явление, которое назвал «новой звездой». Теперь известно, что это был термоядерный взрыв ранее существовавшей звезды, сверхновой типа Ia. Остатки этого взрыва были обнаружены радиоастрономами в 1952 г. на расстоянии примерно в 9000 световых лет – слишком далеко, чтобы до взрыва можно было увидеть эту звезду невооруженным глазом. Тихо наблюдал «новую звезду» в течение нескольких месяцев, используя секстант своей собственной конструкции, и выяснил, что она не демонстрирует суточного параллакса – ежедневного смещения положения небесных тел относительно звезд, которое, как предполагали тогда ученые, связано с вращением Земли (или с ежедневным вращением сферы неподвижных звезд), – который наблюдался бы, если бы эта звезда находилась от Земли на том же расстоянии, что и Луна, или ближе (см. техническое замечание 20). Он пришел к выводу, что «эта новая звезда не располагается ни в верхних слоях воздуха прямо под лунной орбитой, ни в каком-либо другом месте вблизи Земли, а далеко за сферой Луны, на самом небе»[197]. Это полностью противоречило принципу Аристотеля, гласившему, что небеса над орбитой Луны не могут испытывать никаких изменений, и сделало Тихо знаменитым.

В 1576 г. датский король Фредерик II пожаловал Тихо маленький остров Вен, расположенный в проливе между Сконе и большим датским островом Зеландия, а также выделил средства на постройку и содержание дома и научной лаборатории. Тихо построил поместье Ураниборг, где была обсерватория, библиотека, химическая лаборатория и печатный станок. Помещения были украшены портретами великих астрономов прошлого – Гиппарха, Птолемея, аль-Баттани, Коперника – и покровителя науки Вильгельма IV, ландграфа Гессен-Касселя. На Вене Тихо подготовил своих ассистентов и немедленно начал наблюдения.

Уже в 1577 г. Тихо наблюдал комету, у которой тоже не обнаружил никакого суточного параллакса. Это явление шло вразрез не только с положением Аристотеля, утверждающим, что небеса над орбитой Луны не могут меняться. Теперь Тихо также пришел к заключению, что путь кометы пролегал прямо через предполагаемые гомоцентрические сферы Аристотеля или через сферы Птолемея. Конечно, это было невозможным, только если считать сферы твердыми материальными объектами. Именно это положение из учения Аристотеля, как мы видели в главе 8, перенесли в теорию Птолемея астрономы эллинистической эпохи Адраст и Теон. Идея о существовании твердых сфер получила новую жизнь в начале Нового времени[198], незадолго до того, как Тихо доказал, что это невозможно. Кометы появляются чаще, чем сверхновые, поэтому в последующие годы у Тихо был шанс повторить свои наблюдения за другими кометами.

С 1583 г. Тихо работал над новой теорией планет, основанной на том, что Земля находится в состоянии покоя, Солнце и Луна обращаются вокруг нее, а пять известных в то время планет обращаются вокруг Солнца. Эта теория была опубликована в 1588 г. в восьмой главе книги Тихо о комете 1577 г. По этой теории не предполагалось, что Земля вращается или движется, поэтому вдобавок к своему медленному движению Солнце, Луна, планеты и звезды совершали один оборот в сутки вокруг Земли в направлении с востока на запад. Некоторые астрономы приняли вместо этой теории Тихо еще более компромиссную теорию, где планеты обращались вокруг Солнца, Солнце обращалось вокруг Земли, но Земля вращалась, а звезды оставались неподвижными. Первым, кто предложил такую систему, был Николас Реймерс Бэр, который обвинил Браге в том, что тот украл свою гео-гелиоцентрическую систему у него[199].

Как уже несколько раз упоминалось выше, гео-гелиоцентрическая теория Тихо идентична одной из версий теории Птолемея (которую Птолемей никогда не рассматривал), где берутся такие деференты внутренних планет, которые совпадают с орбитой Солнца вокруг Земли, а эпициклы внешних планет имеют тот же радиус, что и орбита Солнца. Поскольку рассматриваются лишь относительные расстояния и скорости небесных тел, теория Тихо также эквивалентна теории Коперника, отличаясь только позицией наблюдателя: неподвижное Солнце – у Коперника и неподвижная Земля – у Тихо. Что касается наблюдений, теория Браге имеет одно преимущество – она автоматически предсказывает отсутствие годичного параллакса звезд, не нуждаясь в предположении о том, что звезды находятся от Земли гораздо дальше, чем Солнце, Луна и планеты (но мы-то, конечно, знаем, что так оно и есть). Она также делает ненужным ответ Орема на классическую проблему, которая сбивала с толку и Птолемея, и Буридана, о том, что тела, брошенные вверх, должны отставать от движения Земли из-за ее вращения, а этого не наблюдается.

Для будущего астрономии самым важным вкладом Браге стала не его теория, а невиданная ранее точность наблюдений. Когда в 1970-е годы я побывал на острове Вен, я не нашел никаких следов построек Тихо, но в земле все еще были массивные каменные основания, на которых Браге крепил свои инструменты (со времени моего визита на острове появился музей и были разбиты сады). С помощью этих инструментов Тихо мог определить положение объектов на небе с погрешностью всего лишь в 1/15°. Кроме того, на месте Ураниборга стоит огромная гранитная статуя, которую в 1936 г. изготовил Ивар Йонссон. Эта скульптура изображает Тихо в положении, приличествующем астроному, – с лицом, обращенным к небу.

Покровитель Тихо Фредерик II умер в 1588 г. Его сменил Кристиан IV, которого ныне живущие датчане считают одним из самых великих королей. Но, к сожалению, Кристиан был совершенно равнодушен к астрономии. Последние наблюдения на Вене Тихо провел в 1597 г., после чего отправился в путешествие, которое привело его в Гамбург, Дрезден, Виттенберг и, наконец, в Прагу. Там он стал придворным математиком Рудольфа II, императора Священной Римской империи, и начал работать над новыми астрономическими таблицами – «Рудольфовыми». После смерти Тихо в 1601 г. эта работа была продолжена Кеплером.

Иоганн Кеплер был первым, кто понял суть несоответствия наблюдаемого движения планет теоретическому движению по кругу с постоянной скоростью, что озадачивало астрономов со времен Платона. Еще пятилетним ребенком, в 1577 г., он был потрясен, увидев комету, ту самую, которую Тихо изучал в своей обсерватории на Вене. Кеплер поступил в университет в Тюбингене, который под руководством Меланхтона специализировался в теологии и математике. В Тюбингене Кеплер изучал оба эти предмета, но больше заинтересовался математикой. Он узнал о теории Коперника от профессора математики из Тюбингена Михаэля Местлина и поверил в ее правильность.

В 1594 г. Кеплер стал учителем математики в лютеранской школе в Граце, в южной Австрии. Именно здесь вышла в свет его первая книга «Тайна мироздания» (Mysterium Cosmographicum). Как мы уже видели, одним из достижений теории Коперника было то, что она позволила с помощью астрономических наблюдений определить уникальный порядок расположения планет и размеры их орбит. Как было принято в те времена, в своей первой работе Кеплер считал эти орбиты окружностями, описываемыми при движении планет, прикрепленных к прозрачным сферам, которые вращались, в соответствии с теорией Коперника, вокруг Солнца. Эти сферы не были строго двумерными, но представляли собой тонкие оболочки, внутренние и внешние радиусы которых он принимал равными минимальному и максимальному расстоянию от планеты до Солнца. Кеплер предположил, что радиусы этих сфер ограничиваются априорным условием – каждая сфера (кроме внешней сферы Сатурна) вплотную вписывается в один из пяти правильных многогранников, и каждая же сфера (кроме самой внутренней, принадлежащей Меркурию) вплотную описывается вокруг другого из того же ряда многогранников. В частности, если идти от Солнца, Кеплер вначале разместил сферу Меркурия, затем – октаэдр, сферу Венеры, икосаэдр, сферу Земли, додекаэдр, сферу Марса, тетраэдр, сферу Юпитера, куб и, наконец, сферу Сатурна. Все это было плотно подогнано друг к другу.

Эта схема задает относительные размеры орбит планет, не оставляя никакой свободы для подгонки результатов, кроме как свободы выбрать порядок пяти правильных многогранников, которые занимают пространство между планетами. Существует 30 различных способов разместить правильные многогранники в определенном порядке[200], но ничего удивительного, что Кеплер выбрал тот способ, при котором предсказанные размеры орбит планет приблизительно соответствовали результатам, полученным Коперником.

На самом деле исходная схема Кеплера плохо работала для Меркурия, что заставило его подгонять ее под ответ, и лишь приблизительно подходила для остальных планет[201]. Но, как и на многих других ученых эпохи Возрождения, на Кеплера оказали большое влияние труды Платона, и, как и Платона, его заинтриговала теорема о том, что существует только пять видов правильных многогранников, оставляя, таким образом, место только для шести планет, включая Землю. Он с гордостью заявлял: «Теперь у нас есть причина, которая может объяснить количество планет!»

Сегодня никто не стал бы принимать схему, похожую на ту, которую предлагал Кеплер, всерьез, даже если бы она работала лучше. Это не потому, что нас не захватывают эмоции Платона, который был потрясен краткостью списков возможных в математике объектов, наподобие последовательности правильных многогранников. Есть и другие короткие списки, которые по-прежнему интригуют физиков. Например, известно, что существует всего четыре «вида» чисел, для которых возможны арифметические действия, в том числе деление: вещественные числа, комплексные числа (в том числе квадратный корень из –1) и более экзотические виды чисел – кватернионы и октонионы. Некоторые физики потратили много усилий, чтобы включить кватернионы и октонионы наряду с вещественными и комплексными числами в фундаментальные законы физики. Схему Кеплера делает такой чуждой для нас не то, что он пытается придать какой-то физический смысл правильным многогранникам, а то, что он пытается объяснить размеры орбит планет, которые являются исторически случайными величинами. Какими бы ни были фундаментальные законы природы, сейчас мы можем быть полностью уверены, что они не соотносятся с радиусами орбит планет.

Но это не было просто глупостью со стороны Кеплера. В его времена никто не знал (и Кеплер не верил), что звезды являются «солнцами» для других планетных систем, они представлялись просто огнями на сфере, расположенной где-то за сферой Сатурна. Солнечная система обычно считалась всей вселенной, существовавшей с начала времен. Поэтому было совершенно естественно полагать, что детальная структура Солнечной системы так же непреложна, как и все остальное в природе.

В современной теоретической физике мы вполне можем находиться в таком же положении. Обычно предполагается, что то, что мы называем расширяющейся Вселенной, все это огромное облако галактик, которое, как мы наблюдаем, разлетается во всех направлениях, и является всей Вселенной. Мы думаем, что физические константы, которые мы измерили, такие как, например, массы различных элементарных частиц, рано или поздно будут выведены из каких-то фундаментальных законов природы, которые пока нам не известны. Но вполне возможно, что то, что мы называем расширяющейся Вселенной, – это только маленькая часть огромного мультиверса, содержащего множество таких же расширяющихся вселенных, как та, которую мы наблюдаем, и что в разных частях этого мультиверса физические константы могут иметь разные значения. В таком случае эти константы являются параметрами среды, которые невозможно вывести из фундаментальных принципов, как и расстояние от планет до Солнца. Лучшее, на что мы можем надеяться, – это оценка исходя из антропного принципа. Среди миллиардов планет в нашей галактике только очень небольшое их число имеет подходящую температуру и химический состав для возникновения жизни, но очевидно, что когда жизнь все-таки возникнет и достигнет в своем развитии «стадии астрономов», то они обнаружат, что находятся на планете, принадлежащей именно к такому меньшинству. Поэтому нет ничего удивительного в том, что планета, на которой мы живем, находится не в два раза дальше от Солнца или ближе к нему. Точно так же кажется, что только очень небольшое число вселенных, составляющих мультиверса, будут иметь физические константы, которые позволяют жизни эволюционировать, но, конечно же, любой ученый обнаружит себя во вселенной, принадлежащей к этому меньшинству. Это предлагалось в качестве объяснения порядка величины темной энергии, о которой упоминалось в главе 8, до того, как темная энергия была открыта[202]. Конечно, в данном случае это явное абстрактное теоретизирование, но оно служит напоминанием о том, что, пытаясь понять законы природы, мы можем столкнуться с таким же точно разочарованием, с каким столкнулся Кеплер, пытаясь определить размеры Солнечной системы.

Некоторые известные физики отвергают идею мультиверса, потому что не могут принять мысль о том, что в природе существуют константы, которые, возможно, никогда не будут получены расчетным путем. Очень может быть, что вся идея мультиверса окажется неправильной, и поэтому, конечно, преждевременно отказываться от попыток рассчитать все физические константы, о которых мы знаем. Но контраргументом к идее мультиверса никак не может являться наше огорчение от того, что мы не можем выполнить эти расчеты. Какими бы в конце концов ни оказались законы природы, нет никаких причин полагать, что они созданы для того, чтобы сделать физиков счастливее.

В Граце Кеплер начал переписываться с Тихо Браге, который прочитал «Тайну мироздания». Тихо пригласил Кеплера приехать к нему в Ураниборг, но Кеплер решил, что это было бы слишком далекое путешествие. Позже, в феврале 1600 г., Кеплер принял предложение Браге и приехал к нему в Прагу, которая с 1583 г. стала столицей Священной Римской империи. Там Кеплер начал изучать собранную Тихо информацию, особенно касающуюся движения Марса, и нашел расхождение в 0,13° с расчетами, построенными на теории Птолемея[203].

Кеплер и Браге не слишком хорошо ладили, и Кеплер вернулся в Грац. Как раз в это время протестанты были изгнаны из Граца, и в августе 1600 г. Кеплер и его семья были вынуждены уехать. Вернувшись в Прагу, Кеплер начал сотрудничать с Тихо в работе над «Рудольфовыми таблицами», новыми астрономическими таблицами, которые должны были заменить «Прусские таблицы» Рейнгольда. После смерти Браге в 1601 г. карьерные проблемы Кеплера были на какое-то время решены, поскольку он стал преемником Тихо на посту придворного математика императора Рудольфа II.

Император очень интересовался астрологией, поэтому в обязанности Кеплера как придворного математика входило составление гороскопов. Эта была работа, в которой он преуспел, еще будучи студентом в Тюбингене, несмотря на свое скептическое отношение к астрологическим предсказаниям. К счастью, у Кеплера оставалось время и для того, чтобы заниматься настоящей наукой. В 1604 г. он наблюдал сверхновую в созвездии Змееносца. Подобного явления в нашей Галактике или около нее после не случалось до 1987 г. В том же году он опубликовал труд «Оптическая часть астрономии» (Astronomiae Pars Optica), посвященный теории оптики и ее приложению к астрономии, включая влияние эффекта рефракции в атмосфере во время наблюдения за движением планет.

Кеплер продолжил работу над теорией движения планет, безуспешно раз за разом пытаясь примирить схему Коперника с точной информацией Браге, добавляя эксцентры, эпициклы и экванты. Он закончил эту работу к 1605 г., но ее публикация была задержана из-за трений с наследниками Тихо. В конце концов в 1609 г. Кеплер опубликовал свои результаты в книге «Новая астрономия, причинно обоснованная, или Небесная физика, основанная на комментариях к движениям звезды Марс».

Часть III «Новой астрономии» вносит существенное уточнение в теорию Коперника – там вводится эквант и эксцентр для Земли. Таким образом, появляется точка, находящаяся с противоположной стороны от центра Земли относительно ее орбиты. Относительно этой точки Земля обращается с постоянной угловой скоростью. Благодаря этому Кеплер избавился от большинства неточностей, которыми изобиловали теории планетного движения со времен Птолемея. Но информация, собранная Браге, была настолько точна, что Кеплер мог видеть: расхождения между теорией и наблюдением по-прежнему остаются.

В какой-то момент Кеплер начал подозревать, что эта задача не имеет решения и что ему следует отказаться от общего для Платона, Аристотеля, Птолемея, Коперника и Браге предположения о том, что планеты движутся по круговым орбитам. Вместо этого он пришел к выводу, что орбиты имеют овальную форму. В конце концов в главе 58 (всего их было 70) «Новой астрономии» Кеплер вывел точное решение. В положении, которое позже стало известно как Первый закон Кеплера, он заключает, что планеты (в том числе и Земля) обращаются по эллиптическим орбитам, при этом Солнце находится в одном из фокусов, а не в центре. Так же как круг может быть полностью определен одной величиной (если не говорить о его положении) – своим радиусом, так и эллипс может быть определен (если не говорить о его положении и ориентации) двумя величинами – длиной малой и большой осей или длиной большой оси и числом, которое называется эксцентриситет, указывающим, насколько различаются большая и малая оси (см. техническое замечание 18). Два фокуса эллипса – это точки на большой оси, равноудаленные от центра и отстоящие друг от друга на расстояние, равное эксцентриситету эллипса, умноженному на длину большой оси. При нулевом эксцентриситете обе оси имеют равную длину, два фокуса сходятся в одной точке и эллипс превращается в окружность.

В действительности орбиты всех планет, известных Кеплеру, имели маленький эксцентриситет, как показано в следующей таблице, где приведены современные (к началу XX в.) значения:

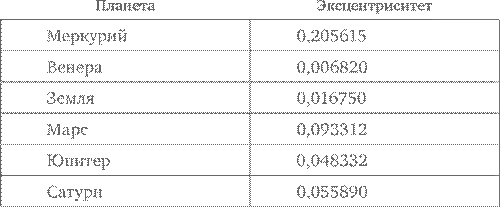
Именно поэтому простейшие версии теорий Коперника и Птолемея (без эпициклов в теории Коперника и только с одним эпициклом для каждой из пяти планет в теории Птолемея) работали достаточно хорошо[204].

Замена круговых орбит эллипсами повлекла серьезные последствия еще по одной причине. Окружности порождаются движением точек на поверхности сферы, но не существует ни одного твердого тела, в результате вращения которого может получиться эллипс. Это вместе с выводами Браге по поводу кометы 1577 г. привело к краху древней идеи о том, что планеты крепятся к вращающимся сферам, идеи, которую сам Кеплер еще допускал в своей «Тайне мироздания». Вместо этого теперь Кеплер и его последователи считали, что планеты двигаются по орбитам, свободно пролегающим в пустоте космоса.

Вычисления, описанные в «Новой астрономии», также использовались для доказательства положения, которое стало позже известно как Второй закон Кеплера, хотя он не был четко сформулирован до выхода в 1621 г. его «Краткого изложения коперниканской астрономии». Второй закон Кеплера объясняет, как скорость планеты меняется по мере ее движения по орбите. Он гласит, что при движении каждой планеты за равные промежутки времени радиус-вектор, то есть линия, соединяющая Солнце и планету, покрывает равные площади. Когда планета находится близко к Солнцу, она должна двигаться быстрее, чтобы покрыть ту же площадь, за равный промежуток времени, оказавшись далеко от Солнца. Таким образом, следствием из Второго закона Кеплера является то, что планеты ускоряются, приближаясь к Солнцу. Если не считать мелких поправок, пропорциональных квадрату эксцентриситета, то Второй закон Кеплера означает, что радиус-вектор от планеты до другого фокуса ее орбиты (того, в котором нет Солнца) вращается с постоянной угловой скоростью – то есть она поворачивается на один и тот же угол каждую секунду (см. техническое замечание 21). Таким образом, с хорошей точностью закон Кеплера дает те же планетные скорости, что и древняя идея экванта – точки, расположенной на противоположной стороне от центра окружности относительно Солнца (или, по Птолемею, относительно Земли) и находящейся на том же расстоянии от центра, вокруг которой линия, ведущая к планете, вращается с постоянной угловой скоростью. Следовательно, эквант оказывается ничем иным как пустым фокусом эллипса. Только великолепная коллекция наблюдений Браге за положением Марса позволила Кеплеру прийти к выводу, что эксцентра и экванта недостаточно и что круговые орбиты должны быть заменены эллиптическими[205].

У Второго закона было также весьма глубокое следствие, по крайней мере для Кеплера. В «Тайне мироздания» Кеплер считал, что планеты движутся из-за «ведущего духа». Но теперь, когда стало понятно, что скорость планеты уменьшается, когда она отдаляется от Солнца, Кеплер пришел к выводу, что планеты приводятся в движение какого-то рода силой, исходящей от Солнца:

«Если заменить слово “дух” (anima) на слово “сила” (vis), то мы получим тот самый принцип, на котором основана небесная физика в “Комментарии к движениям звезды Марс” (Новой астрономии). Некогда я был полностью уверен, что причиной, вызывающей движение планет, является дух – этой мыслью пропитано учение Ж. С. Скалигера[206]о движущих стремлениях. Но поняв, что эта движущая причина ослабевает, когда расстояние до Солнца возрастает, точно так же, как тускнеет солнечный свет, я пришел к выводу, что эта сила должна быть вещественной»[207].

Конечно, планеты двигаются не из-за силы, исходящей от Солнца, а, скорее, потому, что нет ничего, что могло бы лишить их импульса, который они изначально имеют. Но они остаются на своих орбитах, а не улетают в межзвездное пространство благодаря силе, исходящей от Солнца, – силе тяготения, поэтому Кеплер был не так уж не прав. Идея о силе, действующей на расстоянии, была популярна в то время, частично из-за работы по магнетизму Уильяма Гилберта, президента Королевского медицинского колледжа и придворного врача Елизаветы I, на которого Кеплер ссылался. Если Кеплер под «душой» имел в виду одно из обычных значений этого слова, то переход от «физики», основанной на душах, к физике, основанной на действии, был решающим шагом, покончившим с древним засильем религии в естественных науках.

«Новая астрономия» была написана не для того, чтобы избежать разногласий. Использовав в полном заглавии слово «физика», Кеплер бросал вызов старой идее, популярной среди сторонников Аристотеля, о том, что астрономия должна служить только для математического описания явлений, а для настоящего понимания их сути нужно обратиться к физике, а именно к физике Аристотеля. Кеплер поставил на кон утверждение о том, что именно астрономы, как и он сам, занимаются настоящей физикой. На самом деле большая часть рассуждений Кеплера была порождена ошибочной физической идеей о том, что Солнце двигает планеты по их орбитам с помощью некой силы, напоминающей магнетизм.

Кеплер также бросал вызов всем оппонентам учения Коперника. В предисловии к «Новой астрономии» есть следующие слова:

«Совет для идиотов. Но любому, кто слишком глуп, чтобы понять астрономическую науку, или слишком слаб, чтобы поверить Копернику и не оскорбить своей веры, я бы посоветовал прекратить астрономические изыскания и заняться любыми философскими трудами, которые удовлетворят его. Таким образом он займется своим собственным делом и будет сидеть дома и копаться в своем собственном огороде…»[208]

В двух первых законах Кеплера ничего не говорилось о сравнении орбит различных планет. Этот пробел был заполнен в 1619 г. в «Гармонии мира» (Harmonices mundi) положением[209], которое стало в будущем известно как Третий закон Кеплера: «Квадраты периодов обращения любых двух планет относятся между собой как кубы их средних расстояний от Солнца»[210]. Это означает, что квадрат сидерического периода каждой планеты (время, которое ей требуется, чтобы совершить полный оборот по своей орбите) пропорционален кубу длинной оси эллипса. Так, если Т – это сидерический период в годах, а a – половина длины большой оси эллипса в астрономических единицах (а. е.), причем за одну а. е. принимается половина длины большой оси земной орбиты, тогда Третий закон Кеплера гласит, что соотношение T² / a³ будет одинаково для всех планет. Поскольку для Земли Т по определению равен одному году, а a – одной астрономической единице, то T² / a³ =1, соответственно, по Третьему закону Кеплера, для всех планет T² / a³ =1. Точные современные значения подтверждают это правило, что видно в таблице, приведенной ниже:

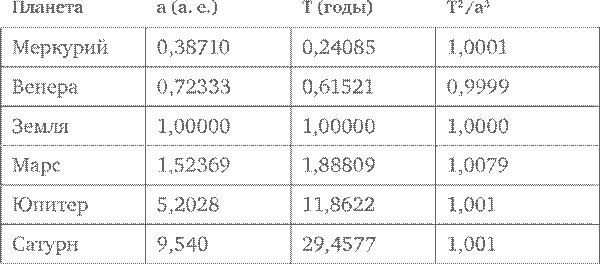
Отклонения от точного равенства соотношения T² / a³ для различных планет вызваны незначительным эффектом, который оказывают друг на друга гравитационные поля самих планет.

Так и не избавившись полностью от восхищения Платоном, Кеплер попытался придать смысл этим размерам орбит, вернувшись к использованию правильных многогранников в «Тайне мироздания». Он также развлекался с пифагорейской идеей о том, что различные планетные периоды формируют что-то вроде музыкальной шкалы. Как и другие ученые своего времени, Кеплер только частично принадлежал к новому миру науки, который лишь зарождался, а частично – к старинной философской и поэтической традиции.

«Рудольфовы таблицы» были закончены только в 1627 г. Основанные на первых двух законах Кеплера, они демонстрировали гораздо более высокую точность по сравнению с предшествующими «Прусскими таблицами». Новые таблицы предсказывали прохождение Меркурия по диску Солнца в 1631 г., которое Кеплеру увидеть не довелось. После того как его как протестанта заставили покинуть католическую Австрию, Кеплер умер в Регенсбурге в 1630 г.

Работы Коперника и Кеплера создали доказательную базу для гелиоцентрической теории, основанной на математической простоте и непротиворечивости, а не только на лучшей согласованности с наблюдением. Как мы уже видели, простейшие версии теорий Коперника и Птолемея дают те же самые предсказания видимого движения Солнца и планет и достаточно хорошо согласуются с наблюдением, и уточнения, внесенные Кеплером в теорию Коперника, могли бы подойти и теории Птолемея, если бы он использовал эквант и эксцентр как для планет, так и для Солнца, и добавил еще несколько эпициклов. Первое решающее подтверждение гелиоцентрической теории наблюдением было сделано Галилео Галилеем.

Галилей был одним из величайших ученых в истории, и достоин стоять в одном ряду с Ньютоном, Дарвином и Эйнштейном. Он произвел революцию в наблюдательной астрономии, создав и использовав телескоп. Его работы по изучению движения создали исследовательскую парадигму для современной экспериментальной физики. Более того (в какой-то степени это уникальный случай), его научная деятельность сопровождалась высокой драмой, о которой здесь мы можем рассказать только очень кратко.

Галилей происходил из благородной, хотя и небогатой тосканской семьи. Он родился в Пизе в 1564 г. в семье теоретика музыки Винченцо Галилея. Поучившись некоторое время в школе при одном тосканском монастыре, он поступил в университет Пизы, чтобы изучать медицину. В этот период жизни он считал себя последователем Аристотеля, что неудивительно для студента-медика. Постепенно интересы Галилея переключились с медицины на математику, и некоторое время он даже давал уроки математики во Флоренции, столице Тосканы. В 1589 г. Галилея пригласили вернуться в Пизу, чтобы занять должность профессора математики.

В университете Пизы Галилей начал свою работу по изучению падающих тел. Часть этой работы описана в трактате «О движении» (De Motu), который он так и не опубликовал. В отличие от Аристотеля Галилей пришел к выводу, что скорость тяжелого падающего тела незначительно зависит от его веса. Очень интересна история о том, как он проводил эксперименты, бросая предметы разного веса с Пизанской башни, но трудно сказать, правдива ли она. Находясь в Пизе, Галилей не публиковал своих работ по падению тел.

В 1591 г. Галилей уехал в Падую, чтобы стать профессором математики в местном университете, который позже под именем Университет Венецианской республики стал одним из выдающихся университетов в Европе. С 1597 г. Галилей дополнял свое университетское жалованье доходом от продажи изготовляемых им математических приборов, которые использовались для производственных и военных целей.

В 1597 г. Галилей получил два экземпляра «Тайны мироздания» Кеплера. Галилео написал Кеплеру, признав в письме, что, как и Кеплер, является сторонником учения Коперника, хотя ранее не высказывал своих взглядов публично. «Вступись, о, Галилео![211]» – воскликнул Кеплер в ответном письме, имея в виду, что Галилей должен встать на сторону Коперника.

Вскоре Галилей начал конфликтовать с аристотелианцами, которые господствовали среди преподавателей философии в Падуе, впрочем, как и во всей Италии. В 1604 г. он читал лекции о «новой звезде», которую в том же году наблюдал Кеплер. Как Браге и Кеплер, Галилей пришел к выводу, что в небесах, над орбитой Луны, действительно происходят изменения. За это он подвергался нападкам человека, которого считал своим другом, – Чезаре Кремонини, профессора философии в Падуе. На эти нападки Галилей ответил, написав на грубом падуанском диалекте диалог между двумя крестьянами. Крестьянин Кремонини утверждал, что обычные правила измерения неприменимы к небесам, а крестьянин Галилей отвечал, что философы ничего не знают об измерениях; и лучше довериться математикам, идет ли речь об измерениях небес или поленты[212].

Революция в астрономии началась в 1609 г., когда Галилей впервые услышал о новом голландском приборе, который назывался «зрительная труба». То, что стекло приобретает способность увеличивать предметы, если стеклянную сферу наполнить водой, было известно еще в античности и упоминалось, к примеру, в трудах римского государственного деятеля и философа Сенеки. Увеличение изучал аль-Хайсам, а в 1267 г. Роджер Бэкон писал об увеличительных стеклах в «Большом сочинении». После усовершенствования производства стекла в XIV в. получили распространение очки для чтения. Но для того, чтобы увеличить изображение далеких объектов, нужна комбинация пары линз: одна – для того, чтобы сфокусировать параллельные лучи света от любой точки объекта так, чтобы они сходились в одной точке, и другая – чтобы собрать эти лучи света вместе. Это можно сделать с помощью либо вогнутой линзы, поместив ее перед точкой схождения лучей после первой линзы, либо с помощью выпуклой линзы, если поставить ее там, где лучи начинают снова расходиться; в любом случае вторая линза посылает лучи в глаз наблюдателя параллельным пучком (в расслабленном состоянии хрусталик глаза фокусирует параллельные лучи света на одной точке сетчатки, местоположение которой зависит от направления параллельных лучей). Зрительные трубы, линзы в которых были сконструированы подобным образом, производились в Нидерландах в начале XVII в., а в 1608 г. несколько голландских производителей обратились за патентами на свои зрительные трубы. Их заявки были отклонены на основании того, что это приспособление уже было широко распространено. Вскоре зрительные трубы появились во Франции и Италии, но они могли увеличивать только в три или четыре раза. Это означает, что если при наблюдении невооруженным глазом две отдаленные точки находятся друг от друга на угловом расстоянии, составляющем определенный небольшой угол, то через зрительную трубу этот угол будет казаться в три или четыре раза больше.

Примерно в 1609 г. Галилей узнал о зрительной трубе и вскоре сделал ее улучшенную версию, где первая линза была с выпуклой передней стороной, плоской тыльной и с большим фокусным расстоянием[213]. Другая линза была вогнутой стороной направлена на первую линзу, вторая сторона была плоской, а фокусное расстояние маленьким. С этими изменениями, чтобы параллельными лучами послать свет точечного источника, расположенного на очень большом расстоянии, в глаз наблюдателя, расстояние между линзами должно было браться как разница между их фокусными расстояниями, а увеличение составляло фокусное расстояние первой линзы, деленное на фокусное расстояние второй (см. техническое замечание 23). Вскоре Галилей смог добиться увеличения в восемь-девять раз. 23 августа 1609 г. он показывал свое изобретение дожу[214]и венецианской аристократии и продемонстрировал, что с помощью этого прибора корабли в море можно заметить на два часа раньше того, как они становятся видны невооруженным глазом. Ценность такого прибора для морской державы, какой была Венеция в то время, была неоспорима. После того как Галилей пожертвовал свой телескоп Венецианской республике, его жалованье было утроено, а постоянная работа в университете гарантирована. К ноябрю Галилей добился увеличения в 20 раз и начал использовать зрительную трубу для астрономических наблюдений.

С помощью своей зрительной трубы, которая позже получила название «телескоп», Галилей сделал шесть астрономических открытий исторической важности. Первые четыре он описал в «Звездном вестнике» (Siderius Nuncius), вышедшем в Венеции в марте 1610 г.:

1. 20 ноября 1609 г. Галилей впервые направил телескоп на полумесяц Луны. На яркой стороне он заметил, что ее поверхность неровная:

«С помощью часто повторяемых наблюдений [лунных пятен] мы пришли к заключению, что поверхность Луны никак не является гладкой и отполированной, как думало множество философов об этом и других небесных телах, но, напротив, неровной и шершавой, а также что на ней, как и на земной поверхности, существуют громадные возвышения, глубокие впадины и пропасти»[215].

На темной стороне, около терминатора (границы дня и ночи) Галилей смог заметить пятнышки света, которые он интерпретировал как вершины гор, освещенные солнцем, когда оно уже готово было взойти над лунным горизонтом. По расстоянию этих ярких пятнышек от терминатора он смог оценить, что некоторые из этих гор достигают по меньшей мере 6 км в высоту (см. техническое замечание 24). Галилей также интерпретировал пепельное свечение затененной части Луны. Он отверг различные предположения Эразма Рейнгольда и Тихо Браге о том, что свет исходит от самой Луны, от Венеры или от звезд, и совершенно верно объяснил, что это «пепельное свечение» связано с освещением лунной поверхности солнечным светом, отраженным от Земли, а Земля ночью точно так же освещается тусклым светом, который является отражением солнечного света от Луны. Таким образом, небесное тело Луна, как оказалось, не так уж сильно отличается от Земли.

2. Зрительная труба позволила Галилею наблюдать «почти немыслимое количество» звезд, намного тусклее шестой звездной величины, то есть слишком тусклых для того, чтобы заметить их невооруженным глазом. Оказалось, что шесть видимых звезд Плеяд окружены более чем 40 другими звездами, а в созвездии Орион Галилей смог разглядеть более 500 звезд, которые никто не видел ранее. Направив телескоп на Млечный Путь, Галилей увидел, что он состоит из множества звезд, как и предполагал Альберт Великий.

3. Галилей сообщил, что в телескоп планеты «представляют свои шарики совершенно круглыми и точно очерченными, как маленькие Луны», но он не смог увидеть подобных изображений у звезд. Вместо этого он узнал, что, хотя звезды, рассматриваемые в телескоп, выглядят более яркими, они не кажутся значительно больше. Его объяснение этого явления было путаным. Галилей не знал, что кажущийся видимый размер звезд вызван преломлением в различных направлениях лучей света в атмосфере Земли, а не чем-либо, присущим самой звезде или ее окружению. Именно из-за этих атмосферных флюктуаций звезды выглядят мерцающими[216]. Галилей решил, что, поскольку невозможно получить изображения звезд с помощью телескопа, они находятся гораздо дальше, чем планеты. Как он отметил позднее, это помогло ему объяснить, почему мы не наблюдаем годичный звездный параллакс, если Земля обращается вокруг Солнца.

4. Самое впечатляющее и важное открытие, описанное в «Звездном вестнике», было сделано 7 января 1610 г. Наведя телескоп на Юпитер, Галилей увидел, что «Юпитеру сопутствуют три звездочки, хотя и небольшие, но очень яркие». Вначале он подумал, что это еще три неподвижные звезды, слишком тусклые, чтобы заметить их раньше, хотя и удивился тому, что они были расположены точно по прямой линии, параллельной эклиптике: две к востоку от Юпитера и одна – к западу. Но следующей ночью все три «звезды» оказались к западу от Юпитера, а 10 января были видны только две, обе на востоке. В конце концов 13 января Галилей увидел четыре такие «звезды», причем все они были расположены более или менее вдоль эклиптики. Он пришел к выводу, что у Юпитера имеется четыре спутника, наподобие земной Луны, которые, как и она, обращаются примерно в плоскости орбиты планеты, которая близка к плоскости эклиптики. Сейчас эти (самые большие) спутники Юпитера известны как Ганимед, Ио, Каллисто и Европа. Они были названы по именам возлюбленных Юпитера[217].

Это открытие стало важным подтверждением теории Коперника. С одной стороны, система Юпитера и его спутников в миниатюре демонстрировала, как, по представлению Коперника, должны выглядеть Солнце и окружающие его планеты. Небесные тела обращались вокруг небесного тела, которое не являлось Землей. Кроме того, существование спутников у Юпитера полностью разрешило вопрос, который задавали противники теории Коперника: если Земля находится в движении, то как Луна не улетает от нее? Все соглашались с тем, что Юпитер двигается, но его спутники явно оставались при нем.

Хотя эти результаты были получены слишком поздно, чтобы включить их в «Звездный вестник», Галилей к концу 1611 г. измерил периоды обращения четырех открытых им спутников Юпитера и в 1612 г. опубликовал их на первой странице труда, посвященного другим вопросам[218]. Сравнение результатов, полученных Галилеем, с современными значениями (в днях, часах и минутах) приводятся в таблице ниже.

Такая точность измерений была достигнута Галилеем путем тщательных наблюдений и точного хронометража[219].

Галилей посвятил свой «Звездный вестник» Козимо II Медичи, бывшему своему ученику, ставшему впоследствии Великим герцогом Тосканы, и назвал четыре спутники Юпитера «Медицейскими звездами». Это был хорошо рассчитанный комплимент. В Падуе у Галилея было неплохое жалованье, но ему сказали, что оно никогда не будет повышено. Кроме того, за это жалованье Галилео должен был преподавать, отнимая время от своих научных изысканий. Он был готов заключить соглашение с Козимо, который называл его придворным математиком и философом, к тому же профессорская должность в Пизе не предполагала обязанностей преподавать. Галилей настаивал на титуле придворного философа, поскольку, несмотря на достижения, которых добились в астрономии такие математики, как Кеплер, и на аргументы таких профессоров, как Клавий, статус математиков был гораздо ниже, чем тот, который имели философы. Также Галилей хотел, чтобы его работы принимали серьезно, как то, что философы называли «физикой», то есть как объяснение природы Солнца, Луны и планет, а не как математическое описание явлений.

Не нашли, что искали? Воспользуйтесь поиском: