Плутон радиусы..... км. 5 страница

Егер Жер бетіне тек Айдың шала көлеңкесі түсетін болса онда оны шала тұтылу деп атаймыз.

Тұтылудың толық фазасының ең үлкен ұзақтығы 7^м 31^с және ол Жер экваторы аймағында Ай көлеңкесі диаметрі максимал (270 км) болғанда болады. Бұндай тұтылу өте сирек болады. 1500 жылдан бері әлі ондай тұтылу болған емес. VII ғасыр мен XVIII ғасыр басы арылығында бұндай бірде бір тұтылу болмайды. Ең жақын арада болатын толық Күн тұтылуы ұзақтығы 7^м 29^с 2186 ж. 16 шілдеде болады.

Сақина тәрізді тұтылудың ең үлкен ұзақтығы 12^м,3 ал шала тұтылу-3^сағ,5. Көбінесе күн тұтылулар 2,5 сағ, ал толық және шала тұтылулар 2-3 минутқа созылады.

Жерде жалпы толық тұтылу ұзақтығы, тұтылу басталу кезінен тұтылу аяқталу кезі аралығы,

1^сағ -3^сағ,5 құрайды, ал осы уақыт аралығында ай көлеңкесі 6000 км-1200 км жолды жүгіріп өтеді.Жерде барлық фазада жалпы Ай тұтылу ұзықтығы 6 сағатқа созылады.

Күн тұтылу фазасы Күн дискісінің ашық бөлігі диаметрінің d оның толық диаметріне d-ге қатнасы арқылы өлшенеді.

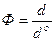
Ай тұтылуы. Ай тұтылу Айдың жердің көлеңкесі арқылы өтуі болатын физикалық құбылыс. Жердің Күннен қашықтығына байланысты Жер көлеңкесі ұзындығы 1359 км-ден 1405000 км-ге созылады, орташа есеппен 1382000 км, яғни бұл Айдың геоцентрлік қашықтығынан әлдеқайда үлкен. Жер көлеңкесі осі Жер орбитасы жазықтығында жатады, сондықтан жер көлеңкесі мен шала көлеңкесі аспанға концентрлі шеңбер түрінде проекцияланады. Бұл концентрлі шеңберлер центрі күнге қарама-қарсы эклиптикада жатады. Сондықтан Ай тұтылу Ай күнге қарама-қарсы тұрғанда, яғни толық ай фазасында ай түйіндері маңайында болуы мүмкін екендігі шығады.

Тұтылулар дәл бұрынғы қалпында қайталануы уақыт аралығы сарос деп аталады.

Сарас 18 жыл 11,3 тәулікке тең.

Сароста 70-71 тұтылу болуы мүмкін, оның 42-43 күн тұтылу,-28-ай тұтылу.

Күн және Ай тұтылу болуы есебептерін және олардың болуы шарттарын мынадай сызба арқылы оңай түсіндіруге болады.

Екі қиылысатын доға жүргіземіз, оның бірі эклиптикаға, екіншісі Ай жолына сәйкес келеді. Ай мен Күннің көрінерлік диаметрлері бірдей 0,⁰5, сондықтан оларды сызбада бірдей диаметрмен көрсеткен. Егер жаңа Ай ай түсінен қашығырақта болса, онда күн тұтылу болмайды. Егер жаңа Ай түйіннен 15⁰ аралықта болса, күн тұтылу болады, және жаңа Ай түйінге жақын болған сайын Күннің көбірек бөлігі Ай дискасымен жабыла түседі. Ақырында түйіннің өзінде ай туса толық немесе сақина тәрізді күн тұтылу болады. 30⁰ доғаны эклиптика бойымен Күн 30,5 тәулікте жүріп өтеді, ал синодтық ай 29,5 тәулік,олай болса 30,5 тәулік ішінде кемінде 1 рет, кейде екі рет жаңа ай болады. Сондықтан жылына түйінде минимум 2 рет күн тұтылу болады. Күн тұтылу жылына минимум 2 рет-максим. 5 рет. Осыған ұқсас Ай тұтылуды да түсіндіруге болады.

Бұл жерде екі негізгі нәрсені еске сақтау керек:.

1) Ай тұтылу толық ай фазасында болуы мүмкін, себебі Жердің көлеңкесі Күнге қарама-қарсы жаққа түседі.

2) Жер көлеңкесі осі төбесі эклиптика бойында Күнге қарама-қарсы жақта жатады.

Бұдан Ай тұтылу айдың толық ай фазасы Ай түйініне жақын болғанда болатындығы көрінеді.Сызбадан 3,2,5,6 орындарда шала ай тұтылу, 4-ші орында толық ай тұтылу, түйіннен қашықтықта ай тұтылу болмайтындығы көрінеді.

Лекция № 6

Аспан механикасы негіздері. Планеталардың қозғалыс заңдарынан кейін мұндай қозғалыстың себебі не деген сұрақ тұрады. Бұл сұрақты шешу алдымен денелердің қозғалыс заңдарын зерттеуді талап етеді. Аспан денелерінің қозғалысын қарастыратын ғылым аспан механикасы деп аталады. Ол Ньютонның ауырлық тартылыс заңына негізделген. Кеплер заңдары осы заңның салдарлары болып табылады.

Ньютонның бүкіл әлемдік тартылыс заңы 1687 жылы жарық көрді.

Ньютон өзінің алдына мынадай сұрақ қойып, оны геометриялық жолмен шешті. Планета бір фокусында Күн орналасқан эллипстік орбита бойымен қозғалады, Күн тарапынан планетаға әсер ететін, эллипс фокусына қарай бағытталған центрге тартқыш күш заңын анықтау қажет.

Бұл есептің шешімі мынада:

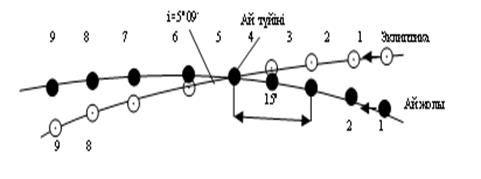
Планетаға түсірілген күш орталық күш деп есептеледі. Кеплердің екінші заңынан планетаның сектролық жылдамдығы тұрақты:

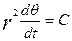
r -планетаның гелиоцентрлік радиус-векторы, Ө-нақты аномалия.

Бұл формуланы мына түрде жазуға болады:

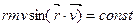
Бұдан сол планетаның Күнге қатысты импульс моментінің модулі:

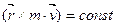
Кеплердің бірінші заңы бойынша планета орбитасы жазық қисық, олай болса импульс моменті шамасы бойынша ғана емес, бағыты бойынша да тұрақты.

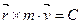
Импульс моменті теоремасы бойынша

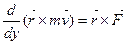
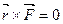
Бұдан планетаның қозғалысы кезінде барлық уақытта 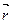және 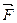векторлары колениарлы, яғни 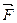күшінің әсер ету түзуі орталық дене (Күн) арқылы өтеді, яғни күш орталық күш.

Осы күштің шамасын анықтау үшін кинетикалық энергияның өзгеруі туралы теоремасын қолданамыз:

Мұндағы m-планета массасы, v-оның жылдамдығы, 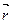-гелиоцентрлік радиус-векторы, 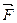-Күн тарапынан планетаға әсер ететін күш. Осы теңдеуді шеше отырып, F-тың мынадай мәнін аламыз

к - пропорционалдық коэффициент.

Күнге планеталардың тарапынан әсер ететін күшінің шамасы:

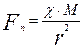
Мұндағы М-Күннің массасы, 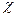- планетаға тән пропорционалдық коэффициент.

Ньютонның үшінші заңына сәйкес

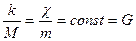
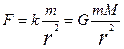
G - гравитациялық тұрақты деп аталады.

Кез келген екі материялық бөлшек олардың массаларына тура пропорционал, ара қашықтығының квадратына кері пропорционал күшпен бір-біріне тартылады.

Екі дене есебі. Табиғи және жасанды аспан денелерінң ілгерілемелі қозғалысының негізгі заңдылықтарын өзара тартылыс күші әсерінен болатын екі дене қозғалысын зерттеу нәтижесінде алуға болады.

Егер екі дененің массасы өзара бірдей болатын болса, онда мұндай есеп жалпы екі дене есебі деп аталады, ал егер бір дененің массасын ескермеуге болатындай болса, онда шектелген екі дене есебі деп аталады.

Практикада бір нүктенің қозғалысын координата басы басқа бір нүктедегі системаға қатысты қарастырған жеткілікті. Сондықтан Sхуz системасын аламыз, оның осьтерінің бағыты өзгермейді, және басы массасы М тартатын S нүктесінде орналасқан болсын. Классикалық механика заңы бойынша m массалы екінші Р нүктесі үшін Ньютонның теңдеуі былай жазылады:

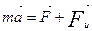
Мұндағы 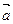-Р нүктесіндегі салыстырмалы үдеуі, 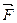-Ньютонның тартылыс күші, 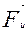-қандай да бір инерциалды санақ жүйесіне қатысты Sхуz системасының үдемелі ілгерілемелі қозғалысынан болатын инерция күші.

Ньютонның тартылыс заңы бойынша

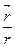Бұл күштің бағыты - бірлік векторы арқылы өрнектеледі.

S нүктесіне қарама-қарсы бағытталған F күші әсер етеді

Онда координата системасының ілгерілемелі қозғалыс үдеуі . Осы үдеуді Р нүктесінің m массасына көбейтіп инерция күшін анықтаймыз:

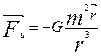
Енді табылған 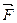және 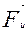күштерінің мәнін орнына қойып,

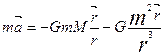
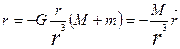(1) аламыз.

Мұндағы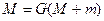

Шектеулі екі дене есебінде m<<M, олай болса

Кеплердің жалпы заңдары. Мына

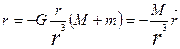(1)

теңдеудің шешімінен шығатын негізгі салдарларды қарастырамыз.

Дифференциялдық (1) теңдеудің мынадай интегралдары бар:

1) Аудан интегралы

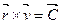(2)

С-импульс моментінің тұрақты векторы. С тұрақты болғандықтан дене орбитасы жазық қисық болады. Егер осы жазықтықта полярлық r және θ координаталарын енгізсек, онда аудан интегралын мына түрде жазуға болады:

(3)

Бұдан Кеплердің екінші заңы шығады.

2)Энергия интегралы

Қозғалыс теңдеуінен (1) энергияның сақталу заңы шығады: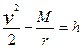

Мұндағы һ-қозғалыстағы дене массасына бөлінген толық механикалық энергияға тең, тұрақты.

Жалпы түрде орбита теңдеуі (яғни (1) теңдеуінің шешімі)

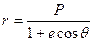(4)

Мұндағы е-эксцентриситет,θ-нақты аномалия.

Эксцентриситеттің шамасы толық энергия мәнімен анықталады және мынаған тең

(5)

h-қозғалыстағы дене массасына бөлінген толық механикалық энергия.

Фокальдық параметр 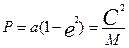(6)

(5) өрнектен траектоияның 3 түрі болатындығы көрінеді.

1)0<e<1 (h<0) немесе (е=0 шеңбер)

2) e=1 (h=0) парабола

3)e>1 (h>0) гипербола

(4) формула Кеплердің жалпы бірінші заңының аналитикалық түрін анықтайды.

Кеплердің үшінші жалпы заңы. Эллипстік қозғалыс үшін сидерлік Т период пен α үлкен ось арасындағы байланысты табуға болады.

Эллипстің ауданы

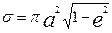, бұны радиус-вектор Т уақытта сызады. (3) формуладан .

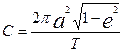Екінші жағынан (6) теңдеуден 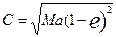. Бұларды теңестіріп

аламыз.

Бұл Кеплердің үшінші жалпы заңы.

Егер М₁ – Күннің массасы, m 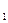- күнді айнала қозғалатын планета массасы болса, ал М₂ басқа бір системадағы планета массасы, ал m 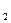оның серігінің массасы болса, онда

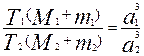егер m₁<<M₁, m₂<<M₂ болса, онда

Кеплердің үшінші заңы.

Нептунның ашылуы. 1781 жылы аспан механикасының ең үлкен жетістігі Нептун планетасының ашылуы болып табылады. Уран деп аталған, бұрын жүздеген жылдар бойы жұлдыз деп есептеліп келген, жаңа үлкен планетаны ағылшын астрономы У.Гершель ашты. Уран координаталары бойынша орбитасын есептегенде оның қозғалысы барлық қозуларды есепке алғанның өзінде кеплерлік қозғалыстан ауытқитындығы анықталды. Бұндай ауытқушылықты түсіндіру үшін осы ауытқушылықты болдыратын тағы да бір белгісіз бір планета бар деген ұсыныс жасалынып, астрономия алдында Уран қозғалысындағы қозу бойынша қоздырушы планета координаттарын анықтау қажеттігі мәселесі туындады. Бұл күрделі математикалық есепті бір мезгілде бір-біріне байланыссыз француз оқымыстысы Леверье мен ағылшын ғалымы Адамс шешті. 1846 жылы 23 қыркүйекте неміс астрономы Галле бұл планетаны Леверрье өзінің есептеуі бойынша көрсеткен аспан нүктесінен 1⁰ –қа жуық қашықтықта тапты. Жаңа планета Нептун деп аталды. Нептунның ашылуы, Энгельстің айтуынша «қалам ұшымен» ашылған, Ньютонның бүкіл әлемдік тартылыс заңының дұрыстығының сенімді дәлелдемесі болып табылды

Тасу және қайту. Жер абсолют қатты дене емес, сондықтан жер бетінің кейбір

бөліктеріне Ай және Күн тарапынан қоздырушы күштер әсері тасу және қайту деп

аталатын құбылыстың пайда болуына әкеледі.

Бұл құбылысты былай түсіндіруге болады. Жер беті су қабатымен (мұхитпен) біркелкі жабылған болсын делік. Ай центрі арқылы өтетін Жер диаметрінде жатқан А және В нүктелеріндегі су бөлшектерін қарастырамыз. Қатты Жер центрінің Т гравитациялық үдеуі

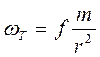
Мұндағы m – Ай массасы, r- Ай центрінің Жер центрінен қашықтығы. А нүктесіндегі мұхит суы үдеуі ω_Т -дан үлкен, ал В нүктесінде ω_Т -дан кіші, яғни

;

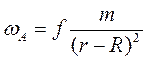
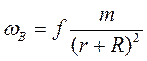Мұндағы R-жер радиусы.

Жер центріне қатысты салыстырмалы үдеу

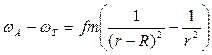немесе ;

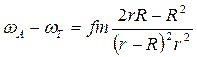Жер радиусы R<< r болғандықтан бөлшек алымындағы R-ты және бөліміндегі (r-R)-дегі R-ді ескермесек, онда

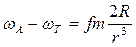аламыз.

Бұл үдеу айырмасы Жер центірінен бағытталған, себебі ω_А > ω_А. В нүктесіндегі үдеу айырмасы ω_В - ω_Т шамасы да дәл осындай және бағыты да ω_В< ω_Т болғандықтан Жер центрінен бағытталған. Сондықтан А және В нүктелерінде Айдың әсері Жер бетіндегі ауырлық күшін азайтады.

Ғ және D нүктелерінде Айдан алатын ω_F және ω_D үдеулері Т нүктесіндегі үдеуге қарама-қарсы үдеуге доғал бұрыш жасай бағытталған, ал тең әсерлі күш Жер центріне қарай бағытталады. Сондықтан Ғ және D нүктелерінде Айдың әсерінен Жердің тартылыс күші артады.

Ғ және А, А және D аралығындағы нүктелерде тең әсерлі үдеу А нүктесіне қарай, ал Ғжәне В, В жәнеD аралығында В нүктесіне қарай бағытталған. Егер осы тең әсерлі күштерді радиус және жанама бағытымен жіктейтін болсақ, онда аралық нүктелерде жердің тартылыс күштерінің аздаған күшейуі немесе әлсіреуі болады. Әсіресе Жердің бір жағында (ҒВD) В нүктесіне бағытталған үдеу ерекше. Осы үдеулердің әсерінен мұхит сулары Жердің бір жартысында Ай зенитте тұрған нүктесіне, ал екінші жартысында Ай надриде түратын нүктесіне ұмтылады.

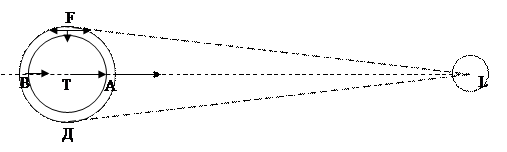Сондықтан, Айдың тартылыс әсерінен Жердің су қабықшасы эллипсоид пішініне келеді де, А және В нүктелері маңайында тасу, ал Ғ және D нүктелері маңайында қайту болады.

Жердің өз осінен айналысы салдарынан тасу биіктіктері әрбір келесі уақыт мезеттерінде жер бетінің жаңа нүктелерінде пайда болады. Сондықтан екі тізбектес Айдың жоғарғы (немесе төменгі) кульминация (жуықтап 24^сағ52^м тең) уақыт аралығында тасу төмпешігі жер шарын айналып шығады және әрбір орында осы уақыт ішінде екі рет тасу және екі рет қайту болады.

Күннің тартылысынан да Жер су қабықшасы қайту және тасуға ұшырайды. Бірақ күндік тасу айлық тасудан 2,2 есе аз. Күннің тасу болдыратын күш үдеуі

мұндағы M₀ - Күн массасы, а- Жердің Күннен қашықтығы.

Айдың тасу болдыратын күш үдеуін осы үдеуге бөлік

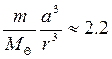аламыз.

Мұнда M₀ =333000М_Т, m= 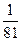, М_Т, а=390 r, М_Т –Жер массасы.

Күндік тасу жеке байқалмайды, олар тек айлық тасу шамасын өзгертеді.

Жаңа ай және толық ай кезінде айлық және күндік тасу бір мезгілде болады да Айдың және Күннің әсері қосылады, және ең үлкен тасу болады. Бірінші және соңғы ширек кезінде (квадратура д. а) айлық тасу мезетіне күндік қайту болады да, Күн әсері Ай әсерінен алынады, ең аз тасу байқалады.

Шындығында тасу және қайту құбылыстары әлдеқайда күрделі. Жер барлық жерінде мұхитпен жабылмаған, тасу толқыны (тасу төмпешігі) мұхит бетімен жүгіре отырып материктердің кұрделі жағалау сызықтарына, әртүрлі пішінді теңіз түбінде кездеседі және үйкеліске ұшырайды. Осы айтқан себептерден тасу болу мезеті Айдың кульминация мезетімен сәйкес келмейді де, бір сағат кейде одан да көп уақыт аралығына кешігеді. Осы уақыт аралығын қолданбалы сағат деп атайды. Тасу биіктіктері әр жерде әртүрлі болады, бірнеше метрден, кейбір жерлерде 10-16 метрге дейін болады.

Тасу құбылысы жер қойнауында да болады. Тасу амплитудасы жер қойнауында бірнеше ондаған сантиметрді құрайды. Сонымен қатар Жер атмосфера қабатында да тасу құбылысы болады.

Тасу үйкелісі Жер айналымын баяулатады, бұл жердің тәулік ұзақтығын жүз жылда 0^с, 0014-қа арттырады.

Жер тарапынан Айда да тасу болады. Айда тасу үдеуі Жердегіден 20 есе үлкен. Тасу әсерінен Айдың Жерге қараған жағы аздап созылынқы.

Лекция № 7

Күн физикасы. Күннің негізгі сипаттамалары.

Күн шеті анық диска түрінде көрінеді. Күн дискасын анықтап қараса оның жарқырауы диска шетіне қарай азая беретінін байқауға болады. Ол әсіресе ультракүлгін сәулелерде күштірек байқалады. Бұл құбылысты шетіне қарай қараю құбылысы деп атайды.Бақылаулар Күн бетінде қараңғы дақтар және олардың топтары бар екендігін сонымен қатар ұсақ дәнге ұқсас – түйіршектер Күн бетін түгел жауып тұратынын көрсетеді. Күннің көрінерлік бетін фотосфера деп атайды.

Толық Күн тұтылу кезінде, яғни Ай Күн дискасын толық жапқанда фотосфера сәулесі көрінбейді де, диска айналасында ені ондаған бұрыштық секундтқа тең жіңішке қызғылт түсті – хромосфера және бірнеше күн радиусына созылған күміс-маржан түсті жарқыраған тәж көрінеді. Хромосфераның толық жарқырауы күннің фотосефрасы жарқырауынан жүздеген есе, ал тәждкінен миллион есе аз.

Хромосфера мен тәжді Күн атмосферасы деп атайды. Күннің бұрыштық және сызықтық өлшемдері фотосефра бойынша анықталады. Жердің Күннен орташа қашықтығы a = 149,6·10⁶ км, осы қашықтықта Күн дискасының бұрыштық радиусы ≈ 16¹, сызықтық радиусы R = 696000 км, яғни Жер радиусынан 109 есе үлкен, ал Ай орбитасы радиусынан жуықтап екі есе үлкен.

Кеплердің ІІІ заңы бойынша анықталған Күн массасы М = 2·10³⁰ кг, Жер массасынан 330000 есе үлкен. Күнде Күн жүйесі барлық массасының 99,87 % жинақталған. Күннің орташа тығыздығы ρ Күн бетінде ауырлық күші үдеуі

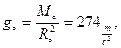жердегіден 28 есе үлкен.

Параболалық жылдамдық

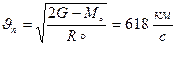
Күннің негізгі сипаттамаларының бірі оның жарқырауы. Ол Күннен Жердің орташа қашықтығында Күн сәулесі энергиясы ағыны интегралдық тығыздығын бақылаудан анықталады. Оны Күн тұрақтысы деп атайды. Күн тұрақтысы дегеніміз атмосферадан тыс шекарада бірлік ауданға бірлік уақытта келіп түсетін энергия. 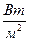немесе 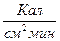өлшенеді. Жердің жасанды серіктері арқылы дәлірек өлшенген күн тұрақтысы мәні:

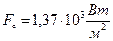
Өлшеулерден Күн тұрақтысы негізінен спектрдің оптикалық диапазонында сәулеленуімен анықталатындығы көрсетіледі. Күннің әрбір секунд сайын шығаратын сәулесі барлық бағытта радиусы а = 149,6 * 10⁹ м сфералық бет арқылы өтеді, олай болса Күннің жарқырауы

Не нашли, что искали? Воспользуйтесь поиском: