
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решение типового примера.
Вопросы к экзамену по математике
1. Первообразная и неопределенный интеграл.
2. Свойства неопределенного интеграла. Таблица основных интегралов.
3. Понятие определенного интеграла и его геометрический смысл.
4. Формула Ньютона-Лейбница.
5. Метод подведения под знак дифференциала.
6. Вычисление площадей плоских фигур.
7. Таблица производных основных элементарных функций. Правила дифференцирования
8. Понятие функции нескольких переменных. Область определения.
9. Частные производные.
10. Частные производные высших порядков.
11. Теорема о смешанной производной.
12. Производная по направлению. Градиент.
13. Экстремум функции нескольких переменных. Необходимое условие экстремума функции нескольких переменных
14. Достаточное условие экстремума функции нескольких переменных.
15. Дифференциальные уравнения. Общие понятия: порядок уравнения, решение,
16. Дифференциальные уравнения 1- го порядка общее и частное решения. Задача Коши
17.. Теорема о единственности решения.
18. Дифференциальные уравнения с разделяющимися переменными,
19. Однородные дифференциальные уравнения 1- го порядка
20. Линейные дифференциальные уравнения 1- го порядка
21. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
Задачи к экзамену
Задание 1
Найти частные производные и частные дифференциалы следующих функций.
1.  2.
2. 
3. 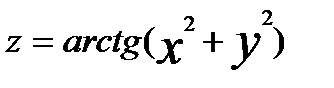 4.
4. 
5. 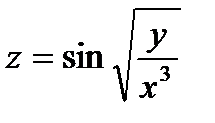 6.
6. 
7. 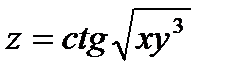 8.
8. 
9.  10.
10. 
11. 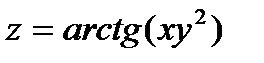 12
12 
13. 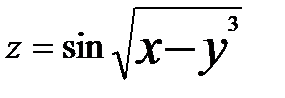 14
14 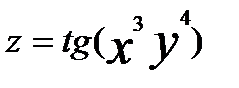
15. 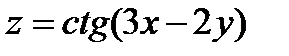 16.
16. 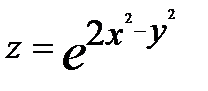
17.  18.
18. 
19. 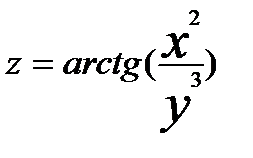 20.
20.  .
.
21.  22.
22. 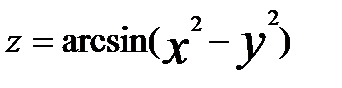
23.  24.
24. 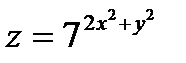
25.  26.
26. 
27.  27.
27. 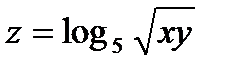
29. 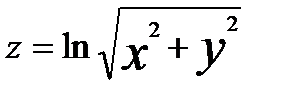 30.
30. 
Задание 2.
Исследовать на экстремум следующие функции
1. 
2. 
3. 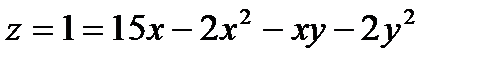
4. 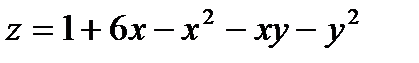
5. 
6. 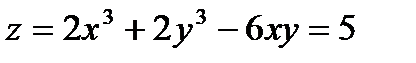
7. 
8. 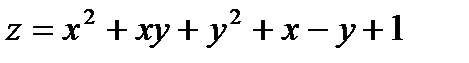
9. 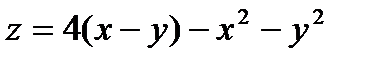
10. 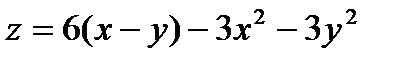
11. 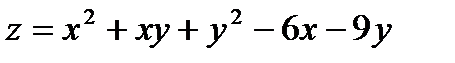
12. 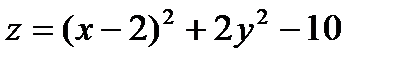
13. 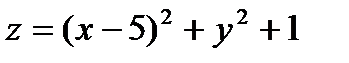
14. 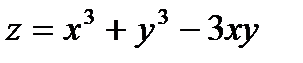
15. 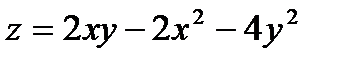
16. 
17. 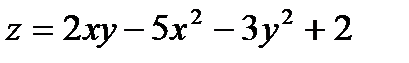
18. 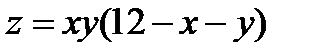
19. 
20. 
21. 
22. 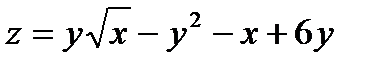
23. 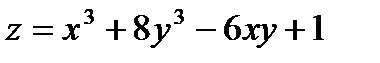
24. 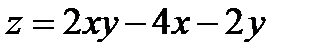
25. 
26. 
27. 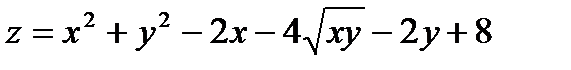
28. 
29. 
30. 
Задание 1.
Найти частные производные и частные дифференциалы функции z=ctg 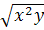
Решение.
Найдем частные производные:
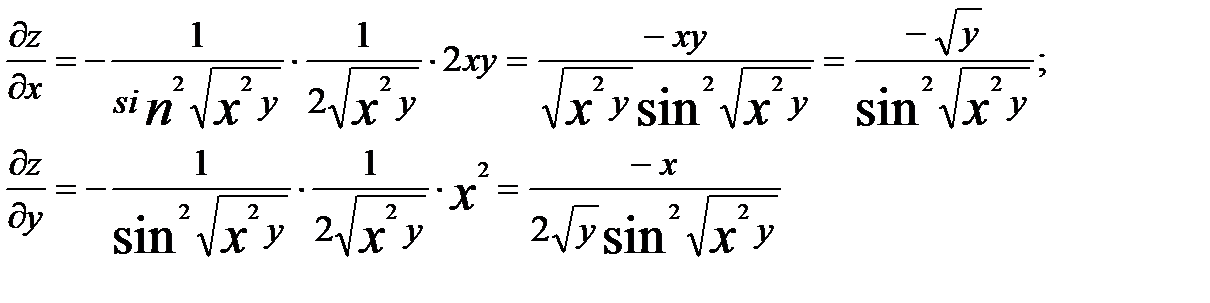
Найдем частные дифференциалы.
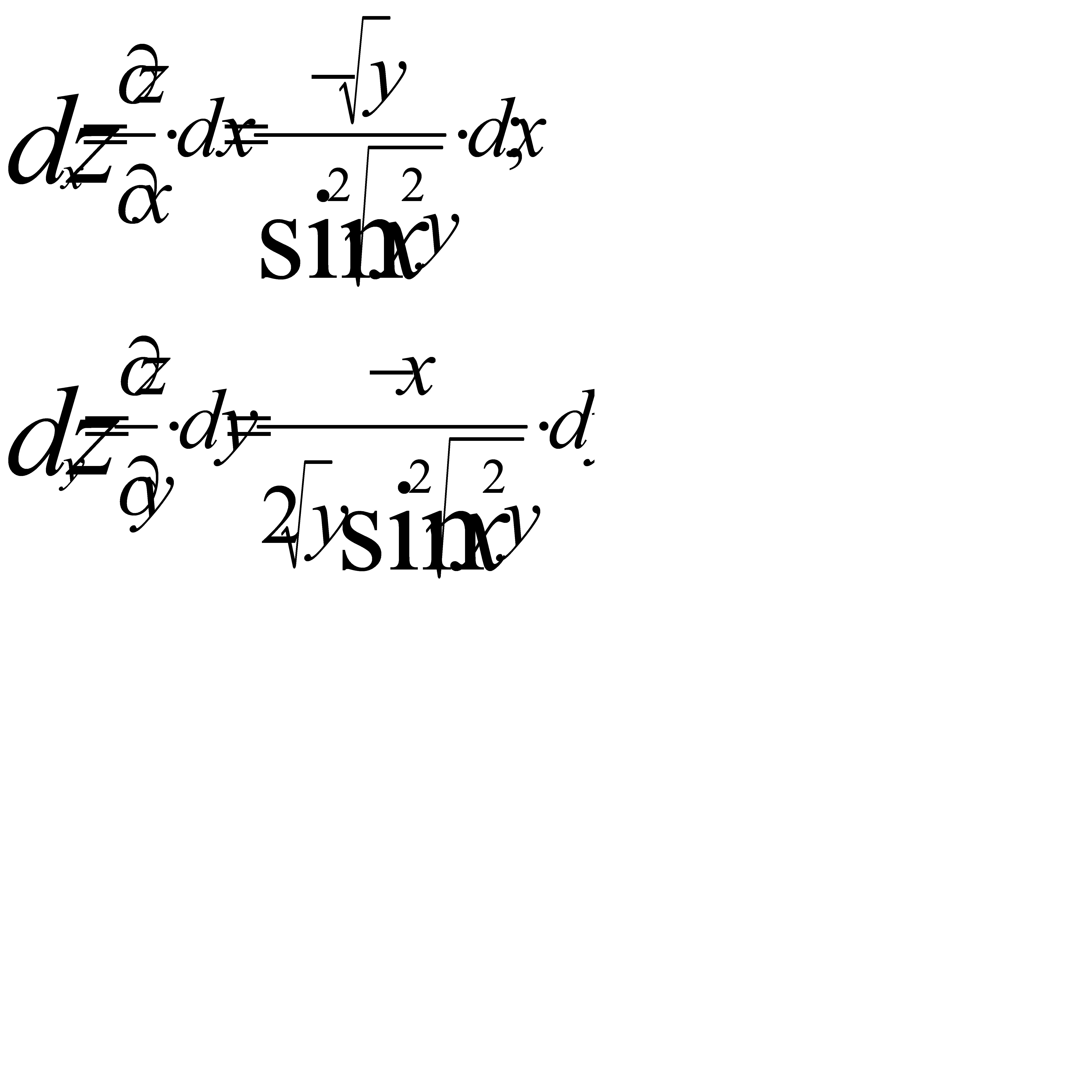
Задание 2.
Исследовать на экстремум функцию 
Решение.
Найдем частные производные:
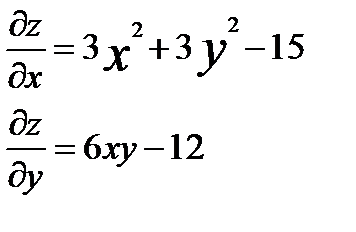
Используя необходимое условие экстремума:

Составим систему уравнений
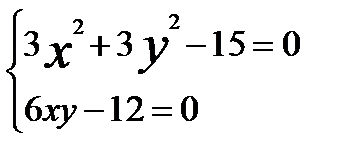
Решив эту систему найдем четыре стационарные точки

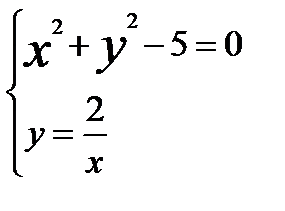
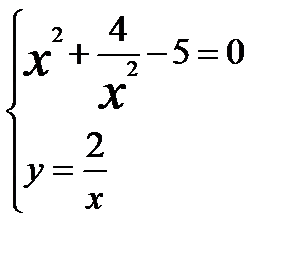
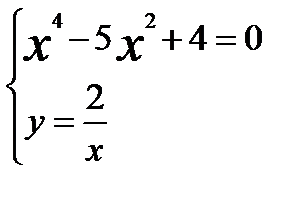
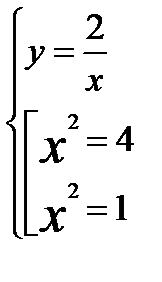

Стационарные точки 
Найдем производные второго порядка

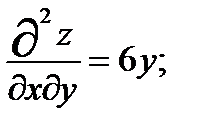

И составим дискриминант 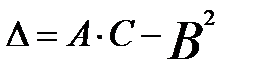 для каждой стационарной точки
для каждой стационарной точки
1) Для точки 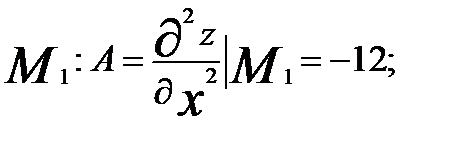



В точке 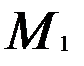 функция имеет максимум, равный
функция имеет максимум, равный 
2) Для точки 
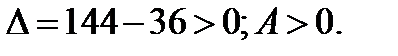
В точке 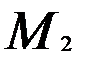 функция имеет минимум, равный
функция имеет минимум, равный 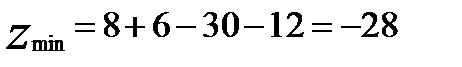
3) Для точки 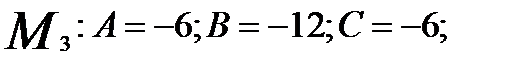
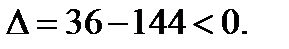 Экстремума нет
Экстремума нет
4) Для точки 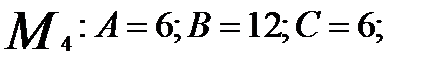
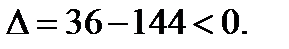 Экстремума нет
Экстремума нет
Интегралы
Типовой пример 1.
Найти неопределенный интеграл:
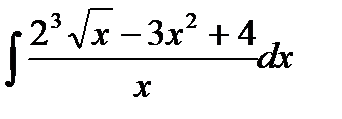
Решение типового примера.
В подынтегральной функции числитель почленно разделим на знаменатель и воспользуемся известными свойствами неопределенного интеграла:
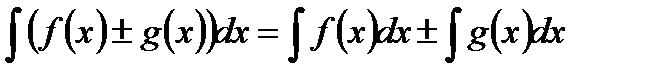 ,
,
 .
.
а также табличными формулами
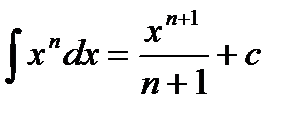
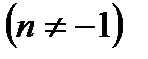 ;
;

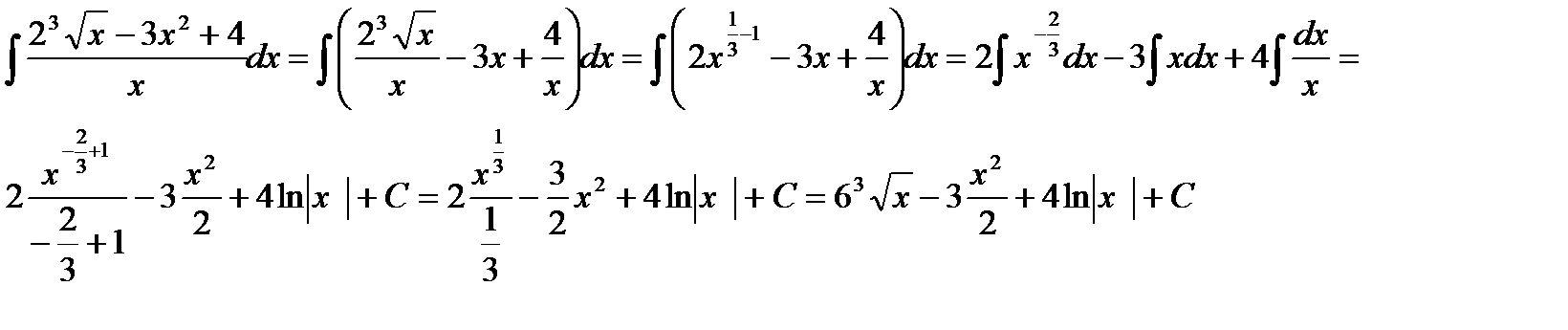
Типовой пример 2.
Найти неопределенный интеграл 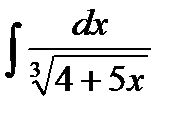 ;
;
Не нашли, что искали? Воспользуйтесь поиском: