
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решение типового примера. y=x2 – квадратичная функция, график парабола, вершина в т
y=x2 – квадратичная функция, график парабола, вершина в т. О (0,0); ветви направлены вверх.
x+y-2=0; y=-x+2 –линейная функция, график прямая.
Найдем точки пересечения линий:
 x1=-2; x2=1; y1=4; y2=1
x1=-2; x2=1; y1=4; y2=1
Схематично изобразим фигуру в прямоугольной системе координат.
Площадь заштрихованной фигуры определяется формулой
S=  где a, b – абсциссы точек пересечения графиков;
где a, b – абсциссы точек пересечения графиков;
f1 (x)- функция, график которой ограничивает фигуру сверху;
f2 (x)- функция, график которой ограничивает фигуру снизу.
Таким образом
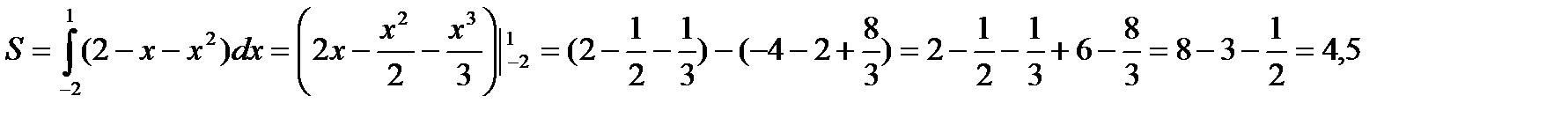 ед2.
ед2.
Расчетные задания,
Задание 1.
Найти неопределенный интеграл:
1. 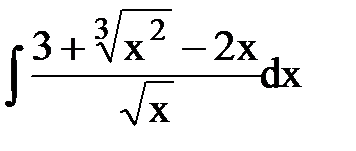 ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  ;
;
5. 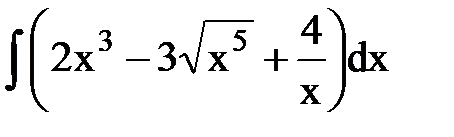 ; 6.
; 6. 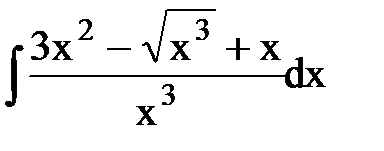 ;
;
7.  ; 8.
; 8.  ;
;
9. 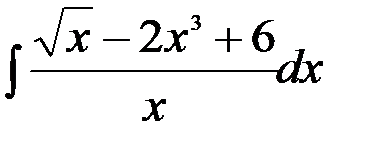 ; 10.
; 10. 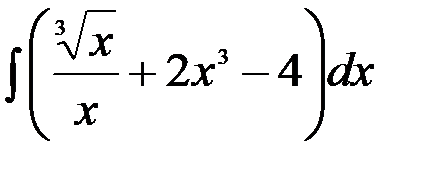 ;
;
11.  ; 12.
; 12.  ;
;
13. 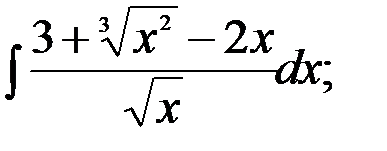 14.
14.  ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18. 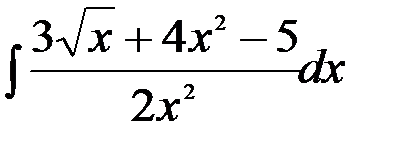 ;
;
19.  ; 20.
; 20.  ;
;
21.  ; 22.
; 22.  ;
;
23.  ; 24.
; 24.  ;
;
25. 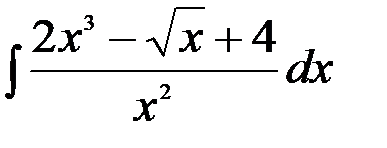 ; 26.
; 26.  ;
;
27.  ; 28.
; 28.  ;
;
 29.
29.  ; 30.
; 30.  ;
;
Задание 2
Найти неопределенный интеграл:
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6. 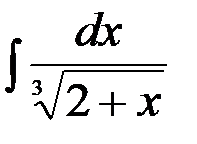 ;
;
7.  ; 8.
; 8. 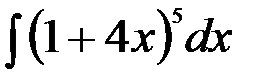 ;
;
9.  ; 10.
; 10.  ;
;
11.  ; 12.
; 12.  ;
;
13. 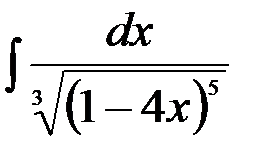 ; 14.
; 14.  ;
;
15.  ; 16.
; 16.  ;
;
17. 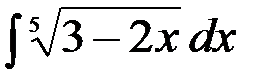 ; 18.
; 18. 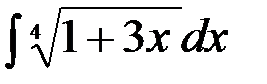 ;
;
19. 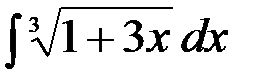 ; 20.
; 20.  ;
;
21. 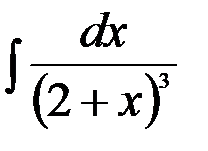 ; 22.
; 22.  ;
;
23.  ; 24.
; 24.  ;
;
25.  26.
26.  ;
;
27. 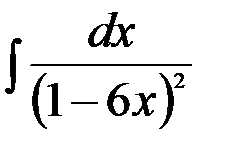 ; 28.
; 28.  ;
;
29.  ; 30.
; 30. 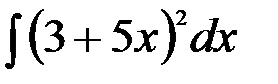 ;
;
Задание 3
Найти неопределенный интеграл
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4. 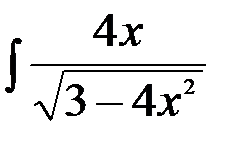 ;
;
5. 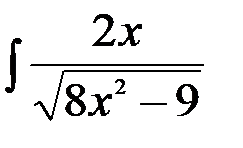 ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ;
;
9.  ; 10.
; 10.  ;
;
11. 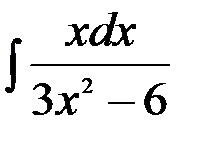 ; 12.
; 12.  ;
;
13. 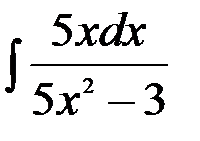 ;
;  14.
14.  ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18. 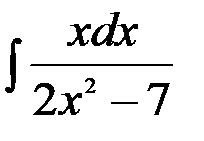 ;
;
19.  ; 20.
; 20.  ;
;
21.  ; 22.
; 22.  ;
;
23.  ; 24.
; 24.  ;
;
25.  ; 26.
; 26.  ;
;
27.  ; 28.
; 28.  ;
;
29.  ; 30.
; 30.  ;
;
Задание 4.
Найти неопределенный интеграл:
1.  ; 2.
; 2. 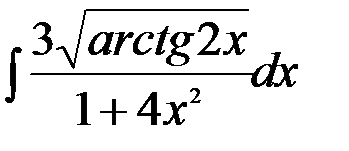 ;
;
3.  ; 4.
; 4.  ;
;
5. 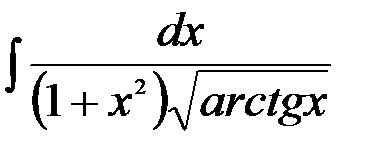 ; 6.
; 6. 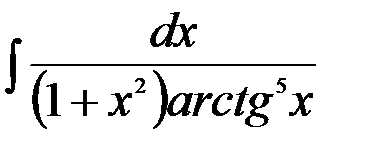 ;
;
7.  ; 8.
; 8.  ;
;
9. 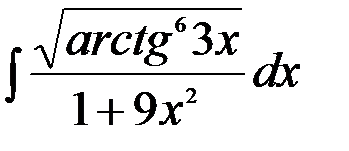 ; 10.
; 10.  ;
;
11.  ; 12.
; 12. 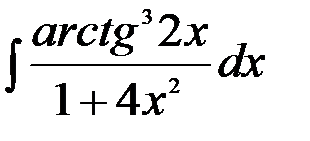 ;
;
13.  ; 14.
; 14. 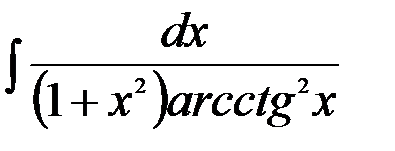 ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18.  ;
;
19.  ; 20.
; 20.  ;
;
21.  ; 22.
; 22.  ;
;
23.  ; 24.
; 24.  ;
;
25.  ; 26.
; 26.  ;
;
27.  ; 28.
; 28.  ;
;
29.  ; 30.
; 30.  ;
; 
Задание 5.
1.Найти неопределенный интеграл:
1.  ; 2.
; 2.  ;
;
3. 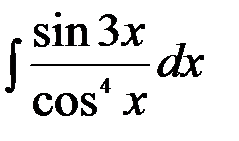 ; 4.
; 4. 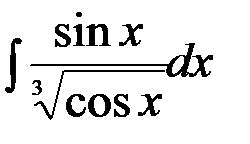 ;
;
5. 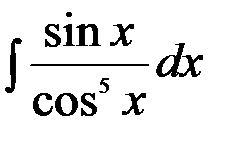 ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ;
;
9. 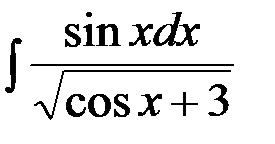 ; 10.
; 10.  ;
;
11. 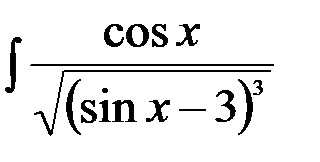 ; 12.
; 12.  ;
; 
13. 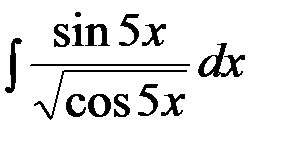 ; 14.
; 14.  ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18.  ;
;
19.  ; 20.
; 20.  ;
;
21.  ; 22.
; 22.  ;
;
23.  ; 24.
; 24.  ;
;
25.  ; 26.
; 26.  ;
;
27.  ; 28.
; 28. 
29.  ;
;
Задание 6.
Вычислить площадь фигуры, ограниченной линиями.
1.  ;
;  ; 2.
; 2.  ;
;
3.  ;
;  ;
;  ; 4.
; 4.  ;
;  ;
; 

5.  ;
; 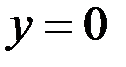 ;
; 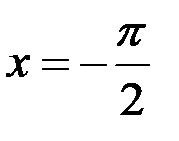 ;
; 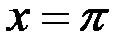 ; 6.
; 6. 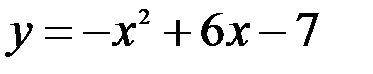 ;
; 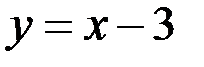 ;
;
7.  ;
;  ; 8.
; 8. 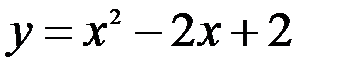 ;
;  ;
;
9.  ;
;  ;
; 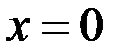 ; 10.
; 10.  ;
;  ;
;
11.  ;
;  ; 12.
; 12.  ;
;  ;
; 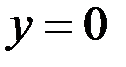 ;
;
13.  ;
;  ;
;  ; 14.
; 14.  ;
; 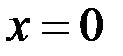 ;
;
15. 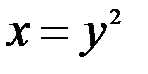 ;
;  ; 16.
; 16.  ;
; 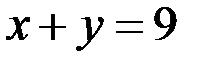 ;
; 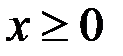 ;
;
17.  ;
; 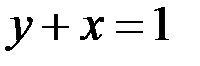 ; 18.
; 18.  ;
; 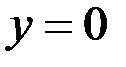 ;
;  ;
;  ;
;
19.  ;
; 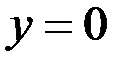 ; 20.
; 20. 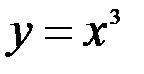 ;
; 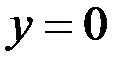 ;
;  ;
;
21.  ;
; 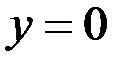 ;
;  ;
;  ; 22.
; 22.  ;
; 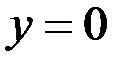 ;
; 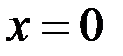 ;
;  ;
;
23. 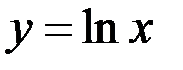 ;
;  ;
;  ; 24.
; 24. 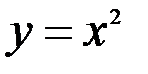 ;
;  ;
;
25.  ;
; 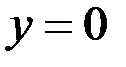 ;
;  ;
;  ; 26.
; 26.  ;y=4;
;y=4;
27.  ;
;  ;
; 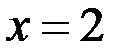 ;
; 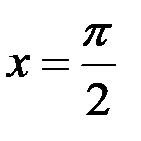 ; 28.
; 28.  ;
;  ;
;  ;
;
29.  ;
;  ; 30.
; 30.  ;
;  ;
;
О Д У
Задание 1. Найти общий интеграл дифференциального уравнения.
1.  2.
2.  ;
;
3.  ; 4.
; 4. 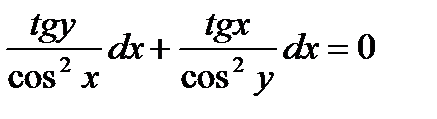 ;
;
5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8. 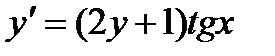 ;
;
9.  ; 10.
; 10.  ;
;
11.  ; 12.
; 12.  ;
;
13.  14.
14.  ;
;
15. 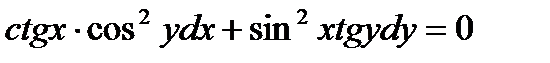 16.
16. 
17.  18
18 
19.  20.
20.  ;
;
21.  22.
22. 
23.  24.
24. 
25.  26.
26. 
27.  28.
28. 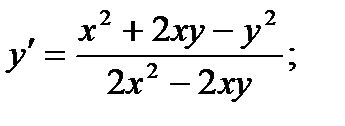
29. 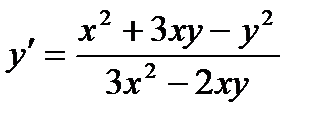 ; 30.
; 30. 
Задание 2. Найти частное решение дифференциального уравнения при следующих начальных условиях.
1. 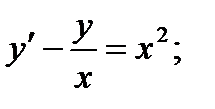
 2.
2. 
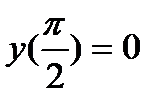 ;
;
3.  ;
; 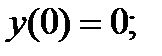 4.
4. 
 ;
;
5. 
 6.
6. 

7. 
 8.
8. 
 ;
;
9. 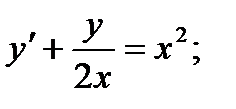
 10.
10. 

11. 
 12.
12. 

13. 
 14.
14. 

15. 
 16.
16. 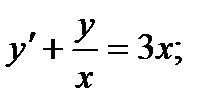

17. 
 18.
18.  ;
; 
19 
 20.
20. 

21. 
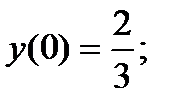 22.
22. 
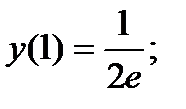
23. 
 24.
24. 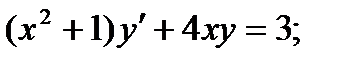
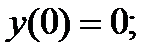
25. 
 26.
26. 

27. 
 28.
28. 

29. 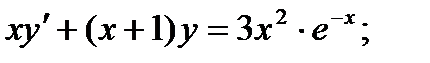
 30.
30. 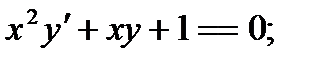

18. В задачах 18.1 – 18.20 найти частное решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям:
18.1. y'' – 7y' + 10y = 0; y(0) = 2; y'(0) = -1.
18.2. y'' + 2y' + 10y = 0; y( ) = 0; y'(
) = 0; y'(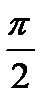 ) = 1.
) = 1.
18.3. y'' – 6y' + 9y = 0; y(0) = 1; y' (0) = 0.
18.4. y'' + 8y' + 7y = 0; y(0) = 2; y'(0) = 1.
18.5. y'' + 9y = 0; y(π) = 0; y'(π) = -1.
18.6. y'' – 7y' + 12y = 0; y(0) = 2; у'(0)=-2.
18.7. y'' + 9y' = 0; y(0) = 1; y'(0) = -3.
18.8. y'' – 3y' + 2y = 0; y(0) = 0; y'(0) = 1.
18.9. y'' – 5y' + 6y = 0; y(0) = 5; y'(0) = 0.
18.10. y'' – 2y' + 5y = 0; y(0) = -1; y'(0) = 0.
18.11. y'' + 16y = 0; y(π) = -1; y'(π) = 0.
18.12. y'' + 10y' + 25y = 0; y(0) = 1; y'(0) = 1.
18.13. y'' – 6y' = 0; y(0) = 2; y'(0) = -2.
18.14. y'' – 4y' + 4y = 0; y(0) = 1; y'(0) = 3.
18.15. y'' – 8y' + 15y = 0; y(0) = 1; y'(0) = -2.
18.16. y'' – 4y' + 17y = 0; y( ) = 0; y'(
) = 0; y'( ) = 1.
) = 1.
18.17. y'' – 2y' + y = 0; y(1) = 0; у'(1)=2
18.18. y'' + y = 0; y(π) = -1; y'(π) = -4.
18.19. y'' – 7y' + 6y = 0; y(0) = 2; y'(0) = 0.
18.20. y'' + 8y' + 16y = 0; y(0) = 1; y'(0) = 0.
Не нашли, что искали? Воспользуйтесь поиском: