
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ПОЯСНЮВАЛЬНА ЗАПИСКА 2 страница
A)8sinα; Б)  ; В)
; В)  ; Г)8соsα.
; Г)8соsα.
1.11 Обчисліть  , якщо
, якщо  = 5,
= 5,  = 4,
= 4,  (a;b) = 30°.
(a;b) = 30°.
А)10 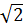 ; Б)10
; Б)10 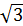 ; В)20
; В)20 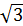 ; Г) 10.
; Г) 10.
1.12 У ∆MNK  K = 45°, МК = 6,
K = 45°, МК = 6,  N = 60°. Знайдіть довжину
N = 60°. Знайдіть довжину
сторони MN.
А) 6  ; Б)2
; Б)2 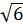 ; В)
; В)  ; Г)3
; Г)3  .
.
Частина друга
Розв'яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
2.1 При яких значеннях х сума дробів  і
і 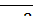 дорівнює їхньому добутку?
дорівнює їхньому добутку?
2.2 Корені x1 і х2 рівняння х2 - 3х + q = 0 задовольняють умову 2х1 - х2 =12. Знайдіть q.
2.3 Знайдіть найменше значення функції у = 4х2 - 12х + 8.
2.4 Пряма, яка паралельна стороні АВ трикутника АВС, перетинає сторони СА і СВ цього трикутника у точках М і N відповідно. АВ = 15 см, МN = 6 см, АМ = 3 см. Знайдіть довжину сторони АС.
Частина третя
Розв'язання задач 3.1-3.3 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1 Відстань між двома пристанями на річці дорівнює 45 км. Моторним човном шлях туди і назад можна подолати за 8 год. Знайдіть власну швидкість човна, якщо швидкість течії дорівнює 3 км/год.
3.2 Доведіть, що коли а, b, с є послідовними членами геометричної прогресії, то виконується рівність
(a 2 +b2)(b2 + с2) = (аb + bс)2.
3.3 Точка дотику кола, вписаного у прямокутний трикутник, ділить катет на відрізки завдовжки 2 см і 3 см, рахуючи від прямого кута. Знайдіть радіус кола, описаного навколо трикутника.
Варіант №6
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на Вашу думку, відповідь і позначте її у бланку відповідей.
1.1 Знайдіть значення виразу 432 ·48 - 38 · 432.
А) 8 941 536; Б) 3420; В) 37 152; Г) 4320.
1.2 Знайдіть суму 
А)  .; Б)
.; Б)  .; В)
.; В)  .; Г)
.; Г)  .
.
1.3 Запишіть вираз a2 - 8ab + 16b2 у вигляді квадрата двочлена.
А) (а – 4b)2; В) (а + 4b)2;
Б) (а2 – 16b2)2; Г) (а – 4b)(а + 4b).
1.4 Укажіть функцію, яка не є лінійною функцією.
А)у = 5; Б) у = 5+  ; В)у = -5х; Г)у = 5х+1.
; В)у = -5х; Г)у = 5х+1.
1.5 Знайдіть корені квадратного рівняння -х2 + 5х - 6 = 0.
А) -2; -3; Б)2;3; В)-6;1; Г)-1;6.
1.6 Скоротіть дріб 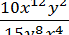 .
.
A)  Б)
Б)  В)
В)  Г)
Г) 
1.7 На якому з рисунків зображено графік функції у = (х + 3)2?


1.8 Яке із чисел є розв'язком нерівності х2 + х - 2 > 0?
А)-2; Б) 2; В) 1; Г)-1.
1.9 Знайдіть бічну сторону рівнобедреного трикутника, якщо його периметр дорівнює 58 см, а основа - 18 см.
А) 40 см; Б) 22 см; В) 20 см; Г) 44 см.
1.10 У ромбі сторона дорівнює 8 см, а більша діагональ - 12 см. Знайдіть довжину меншої діагоналі ромба.
А)2  см; Б) 10 см; В) 4
см; Б) 10 см; В) 4  см; Г)
см; Г) 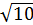 см.
см.
1.11 Який з векторів колінеарний вектору  (2; 3)?
(2; 3)?
А) 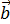 (6;9); Б)
(6;9); Б)  (3;4); В)
(3;4); В)  (1;2); Г)
(1;2); Г)  (9;6).
(9;6).
1.12 Знайдіть відстань від початку координат до середини відрізка АВ, якщо
А(3; -2), В(-1; 4).
А) 2; Б) 13; В)  ; Г)
; Г)  .
.
Частина друга
Розв'яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
2.1 Обчисліть значення виразу 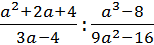 , якщо а=10.
, якщо а=10.
2.2 Знайдіть найбільше ціле число, яке є розв'язком системи нерівностей

2.3 Спростіть вираз  , якщо
, якщо 
2.4 Хорда, довжина якої 8 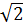 см, стягує дугу кола, градусна міра якої 90°. Знайдіть довжину кола.
см, стягує дугу кола, градусна міра якої 90°. Знайдіть довжину кола.
Частина третя
Розв'язання задач 3.1-3.3 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1 Поїзд, затриманий на 1 год, на перегоні завдовжки 300 км ліквідував запізнення, збільшивши швидкість на 10 км/год. Знайдіть, за який час поїзд мав проїхати даний перегін із початковою швидкістю.
3.2 Знайдіть область визначення функції 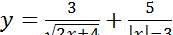
3.3 Довжина кола, описаного навколо рівнобедреного трикутника, дорівнює 50л: см. Знайдіть периметр трикутника, якщо висота, проведена до основи, дорівнює 32 см.
Варіант №7
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на Вашу думку, відповідь і позначте її у бланку відповідей.
1.1 Порівняйте величини 24 хв і  год.
год.
А) 24 хв >  год; В) 24 хв <
год; В) 24 хв <  год;
год;
Б) 24 хв 
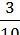 год; Г) 24 хв =
год; Г) 24 хв = 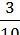 год.
год.
1.2 Знайдіть корінь рівняння 84 - 3х = 12.
А) 32; Б) 288; В) 24; Г) 216.
1.3 Подайте добуток (3x-2)(9х2 + 6x + 4) у вигляді многочлена.
А) (3х - 2)3; В) 27х3 – 12x + 8;
Б) 27х3 - 6х + 8; Г) 27x3 - 8.
1.4 Яке з рівнянь рівносильне рівнянню -10x - 7 = 13?
А) -5+7х=1; Б) -2х + 5 = 9; В) -4х-2 = -11; Г)3x - 9 = 10.
1.5 Чому дорівнює сума коренів квадратного рівняння х2 + 9х - 5 = 0?
А) 9; Б) 5; В)-9; Г)-5.
1.6 Обчисліть значення виразу  .
.
А) 8; Б)2+4  ; В)8 + 4
; В)8 + 4  ; Г) 2.
; Г) 2.
1.7 Знайдіть нулі функції y = 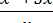
А)0;-5; Б)-5; В)0; Г)5.
1.8 Розв'яжіть нерівність (2x + 4)(х - 3)  0.
0.
А)(-2;3); Б)[-3;2]; В)[-2;3]; Г) (-∞; -2] 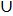 [3; +∞).
[3; +∞).
1.9 Укажіть геометричне місце точок, розміщених на відстані 5 см від даної точки А.
А) круг; Б) пряма; В) відрізок; Г) коло.
1.10 У ромбі ABCD кут ABD дорівнює 75°. Чому дорівнює кут ABC?
А) 75°; Б) 30°; В) 140°; Г) 150°.
1.11 У рівнобедреному трикутнику бічна сторона дорівнює 8 см, а кут при основі - 30°. Знайдіть площу трикутника.
А) 16 см2; Б)32 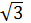 см2; В) 32 см2; Г) 16
см2; В) 32 см2; Г) 16 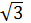 см2.
см2.
1.12 Знайдіть площу трикутника, периметр якого 24 см, а радіус кола, вписаного в цей трикутник, дорівнює 4 см.
А) 96 см2; Б) 24 см2; В) 32 см2; Г)48см2.
Частина друга
Розв'яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
2.1 Спростіть вираз 
2.2 Знайдіть область визначення функції y= 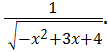
2.3 Розв’яжіть систему рівнянь 
2.4 Дві сторони трикутника відносяться як 5: 3, а кут між ними дорівнює 120°. Знайдіть третю сторону трикутника, якщо його периметр дорівнює 45см.
Частина третя
Розв'язання задач 3.1-3.3 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1 Дві бригади, працюючи разом, зорали поле за 6 днів. За скільки днів може зорати поле кожна бригада, працюючи самостійно, якщо другій бригаді на це потрібно на 5 днів менше, ніж першій?
3.2 Розв'яжіть рівняння 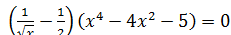
3.3 Знайдіть площу паралелограма, діагоналі якого дорівнюють 8 см і 10 см та одна з діагоналей перпендикулярна до сторони.
Варіант №8
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на Вашу думку, відповідь і позначте її у бланку відповідей.
1.1 Виконайте ділення  :
:  .
.
А)  ; Б) 8; В)
; Б) 8; В)  ; Г)
; Г)  .
.
1.2 Відстань між містами на карті 6,4 см. Знайдіть відстань між цими містами на місцевості, якщо масштаб карти 1: 2 000 000.
А) 12,8 км; Б) 32 км; В) 128 км; Г) 3,2 км.
1.3 Укажіть пару чисел, яка є розв'язком рівняння х - у = 7.
А)(6; 1); Б)(1; 6); В)(6; -1); Г)(-1; -6).
1.4 Графік якого рівняння проходить через точку А(2; -2)?
А) 0 · х - 0 · у = 4; В) 2х + 0 · у = - 4;
Б)0·х + 2у = -4; Г)2х + 2у = 8.
1.5 Виконайте ділення  .
.
А)4а3; Б)  ; В) 4а10; Г)
; В) 4а10; Г)  .
.
1.6 Запишіть число 328 000 000 у стандартному вигляді.
А)3,28 ·108; В) 0,328 ·109;
Б) 328·106; Г)32,8·107.
1.7 Який відсоток жирності молока, якщо з 250 кг молока отримали 15 кг жиру?
А) 60%; Б) 6%; В) 94%; Г)160%.
1.8 Яка з наведених систем нерівностей не має розв'язку?
А) 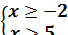 Б)
Б)  В)
В)  Г)
Г) 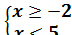
1.9 На якій відстані від кінців відрізка завдовжки 70 см лежить точка, яка поділяє його на дві частини у відношенні 5: 2?
А) 56 см, 14 см; В) 50 см, 20 см;
Б) 14 см, 56 см; Г) 50 см, 70 см.
1.10 Знайдіть довжини відрізків, на які ділить середню лінію діагональ трапеції, основи якої дорівнюють 4 см і 10 см.
А) 2 см і 5 см; В) 3 см і 5 см;
Б) 2 см і 4 см; Г) 4 см і 5 см.
1.11 Знайдіть міру внутрішнього кута при вершині правильного шестикутника.
А) 150°; Б) 100°; В) 90°; Г) 120°.
1.12 Коло вписано у правильний шестикутник зі стороною 4  см. Знайдіть площу круга, обмеженого даним колом.
см. Знайдіть площу круга, обмеженого даним колом.
А) 6  см2; Б) 36
см2; Б) 36  см2; В) 48
см2; В) 48  см2; Г) 16
см2; Г) 16  см2.
см2.
Частина друга
Розв'яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
2.1 Обчисліть 0,75-2 -1,5 -3 - (-3)0.
2.2 Графіком квадратичної функції є парабола, що має вершину у початку координат і проходить через точку А(2; -8). Задайте цю функцію формулою.
2.3 Знайдіть суму перших семи членів геометричної прогресії (bn), якщо
b2 = 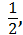 b3 =
b3 =  .
.
2.4 У ∆ ABC  C = 90°, АС = 8 см, sin А =
C = 90°, АС = 8 см, sin А =  . Знайдіть довжину гіпотенузи трикутника.
. Знайдіть довжину гіпотенузи трикутника.
Частина третя
Розв'язання задач 3.1-3.3 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1 Знаменник звичайного нескоротного дробу на 3 більший від чисельника. Якщо чисельник цього дробу збільшити на 2, а знаменник - на 10, то дріб зменшиться на 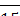 . Знайдіть цей дріб.
. Знайдіть цей дріб.
3.2 Побудуйте графік функції 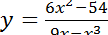 .
.
3.3 Периметр паралелограма дорівнює 26 см, а його діагоналі дорівнюють
7 см і 11 см. Знайдіть сторони паралелограма.
Варіант №9
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на Вашу думку, відповідь і позначте її у бланку відповідей.
1.1 Яку частину години становить 17 хв?
А)  год; Б)
год; Б)  год; В)
год; В)  год; Г)
год; Г)  год;
год;
1.2 Користуючись рисунком, запишіть координати точки М.

А) (-2; 4); Б) (4; 2); В) (-4; -2); Г) (4; -2).
1.3 Яке з рівнянь має безліч коренів?
А)0·х = 3; В) 3х-3 = 0;
Б)3(х- 1) = 3х-3; Г)3х-3 = 3.
1.4 Графіком якої з функцій є пряма, паралельна графіку
функції у = 2х- 5?
А)у = х-5; Б) у=10 + 2х; В) у=-2х - 5; Г) у = -5х.
1.5 Піднесіть до степеня 
А)  Б)
Б)  В)
В)  Г)
Г) 
1.6 Обчисліть значення виразу  .
.
А) 18; Б)-2; В) 5 -  ; Г) 12.
; Г) 12.
1.7 Знайдіть суму перших восьми членів арифметичної прогресії (ап), якщо а1 = 2,5, d = -2.
А) 56; Б) 72; В)-36; Г)-72.
1.8 Розв'яжіть нерівність -3х - 15 < 0.
А) (5; +∞); Б) (-5; +∞); В) (-∞; -5); Г) (-∞; 5).
 1.9 Якими є кути 1 та 2, зображені на рисунку?
1.9 Якими є кути 1 та 2, зображені на рисунку?
А) прямими; В) тупими;
Б) суміжними; Г) вертикальними.
1.10 Знайдіть центральний кут, якщо відповідна йому дуга становить  кола.
кола.
А) 120°; Б) 60°; В) 90°; Г) 30°.
1.11 Точка М - середина відрізка АВ. Знайдіть координати точки М, якщо А(2; -3), В(-6; 7).
А) (4; -5); Б) (-2; 2); В) (2; -2); Г) (-4; 4).
1.12 У гострокутному трикутнику МNР  Р = 45°, МN=4
Р = 45°, МN=4  см, і
см, і
NР = 4  см. Знайдіть
см. Знайдіть  М трикутника МNР.
М трикутника МNР.
А) 75°; Б) 45°; В) 30°; Г)60°.
Частина друга
Розв'яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
2.1 Обчисліть  .
.
2.2 На прямій у = 10 - 3х знайдіть точку, ордината якої удвічі більша за абсцису.
2.3 У сплаві 60 % міді, а решта 200 г становить олово. Яка маса сплаву?
2.4 Модуль вектора  (p + 1; -3) дорівнює 5. Знайдіть р.
(p + 1; -3) дорівнює 5. Знайдіть р.
Частина третя
Розв'язання задач 3.1-3.3 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1 Щоб ліквідувати запізнення на 24 хв, поїзд на перегоні завдовжки 180 км збільшив швидкість на 5 км/год порівняно зі швидкістю за розкладом. Якою є швидкість поїзда за розкладом?
3.2 Для деяких чисел а, b і с, жодне з яких не дорівнює нулю, виконується рівність ( а + b + c)(a - b + с) = a2 +b2+c2. Доведіть, що a, b, c - послідовні члени геометричної прогресії.
3.3 Центр кола, описаного навколо трапеції, належить більшій основі. Знайдіть кути трапеції, якщо основи відносяться як 1: 2.
Варіант №10
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на Вашу думку, відповідь і позначте її у бланку відповідей.
1.1 Обчисліть 48,5 · 0,1 + 48: 1,6.
А) 515; Б) 34,85; В) 7,85; Г) 351,875.
1.2 Знайдіть найбільший спільний дільник чисел 72 і 48.
А) 12; Б) 8; В) 48; Г) 24.
1.3 Перетворіть у многочлен вираз 2a(b – 3c).
A) 2ab - 3с; Б) 2ab - 3ac; В) 2ab · 3с; Г) 2ab - 6ас.
1.4 Подайте у вигляді многочлена вираз (х + 2у)2.
А) х2 + 4у2; В) х2 + 4ху + 2у2;
Б) х2 + 2ху + 2 y 2; Г) x2 + 4ху + 4у2.
1.5 Знайдіть значення виразу 
А)  Б)1; В)
Б)1; В)  Г)-2.
Г)-2.
1.6 Виконайте віднімання  .
.
А)  ; Б)
; Б)  ; В)
; В)  ; Г)
; Г)  .
.
1.7 Знайдіть суму перших п'яти членів арифметичної прогресії (an), якщо
а1 = 3, d = -2.
А) -4; Б) 20; В) -5; Г) -10.
1.8 У коробці лежать 5 зелених, 7 жовтих і 3 червоних кульки. Яка ймовірність того, що навмання витягнута з коробки кулька буде не зеленого кольору?
А)  ; Б)
; Б)  ; В)
; В) 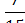 ; Г)
; Г)  .
.
 1.9 На рисунку зображено паралельні прямі а і b, які перетинає січна d. Користуючись рисунком, знайдіть
1.9 На рисунку зображено паралельні прямі а і b, які перетинає січна d. Користуючись рисунком, знайдіть  , якщо
, якщо  2 = 60°.
2 = 60°.
А) 60°; Б) 120°; В) 30°; Г) 150°.
1.10 Укажіть правильну рівність.
А) соs 0° = 0; Б) sin 90° =0; В) sin 30° =  ; Г) соs 45°=
; Г) соs 45°=  .
.
1.11 Знайдіть модуль вектора  (4; 3).
(4; 3).
А) 7; Б)1; В) 5; Г) 25.
1.12 Знайдіть координати вектора  , якщо
, якщо  =3
=3 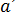 - 2
- 2  ,
,  (-1; 1),
(-1; 1), 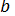 (2;-3).
(2;-3).
А) (7; 9); Б) (-7; 9); В) (-7;-9); Г)(7;-9).
Частина друга
Розв'яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
2.1 Розв'яжіть рівняння х3 + 2х2 - х - 2 = 0.
2.2 Один з коренів рівняння x2 + px- 6 = 0 дорівнює 1,5. Знайдіть р і другий корінь рівняння.
2.3 Знайдіть найбільше значення функції у = -2х2 + 8x - 5.
2.4 Знайдіть довжину медіани АМ трикутника ABC, якщо А(5;-1), В(-4;3), С(6; 1).
Частина третя
Розв'язання задач 3.1-3.3 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1 Сплав золота зі сріблом містить 20 г золота. До цього сплаву додали 5 г срібла і 10 г золота. Отриманий сплав містить на 5 % більше срібла, ніж початковий. Скільки грамів срібла було в початковому сплаві?
3.2 Знайдіть імовірність того, що взяте навмання двоцифрове число кратне 4 або 5.
3.3 Точка дотику кола, вписаного у прямокутний трикутник, ділить гіпотенузу на відрізки завдовжки 4 см і 6 см. Знайдіть периметр трикутника.
Варіант №11
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на Вашу думку, відповідь і позначте її у бланку відповідей.
1.1 Обчисліть значення виразу (1865 - 365): 50.
А) 300; Б) 75 000; В) 30; Г) 7500.
1.2 Знайдіть суму 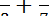 .
.
А)  ; Б)
; Б)  ; В)
; В)  ; Г)
; Г)  .
.
Не нашли, что искали? Воспользуйтесь поиском: