
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ПОЯСНЮВАЛЬНА ЗАПИСКА 4 страница
1.12 Знайдіть координати точки перетину прямих у - х = 2 та х + у = 4.
А)(1;3); Б)(3;1); В)(-1;3); Г)(-3;-1).
Частина друга
Розв'яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
2.1 Скоротіть дріб 
2.2 Знайдіть найбільше ціле значення х, при якому різниця дробів
 і
і  є додатною.
є додатною.
2.3 Знайдіть область визначення функції y= 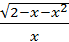
2.4 Знайдіть радіус круга, якщо площа сектора цього круга дорівнює 20  см2, а центральний кут, що відповідає цьому сектору, дорівнює 72°.
см2, а центральний кут, що відповідає цьому сектору, дорівнює 72°.
Частина третя
Розв'язання задач 3.1-3.3 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1 Турист проплив моторним човном проти течії річки 18 км, а повернувся назад на плоту. Човном турист плив на 4,5 год менше, ніж плотом. Знайдіть швидкість течії, якщо швидкість човна у стоячій воді 15 км/год.
3.2 Знайдіть найменший за модулем член арифметичної прогресії
-15,1; -14,4...
3.3 Основи трапеції дорівнюють 2 см і 18 см, а діагоналі - 15 см і 7 см. Знайдіть площу трапеції.
Варіант №17
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на Вашу думку, відповідь і позначте її у бланку відповідей.
1.1 Запишіть 3 год 24 хв у хвилинах.
А)27хв; Б)324хв; В) 204 хв; Г) 54 хв.
1.2 Виконайте множення  .
.
А)6; Б) 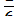 ; В)
; В)  ; Г) 3
; Г) 3 
1.3 Знайдіть значення аргументу,при якому функція у=-5 +4х має значення 3.
А) - 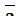 ; Б)2; В) 7; Г)
; Б)2; В) 7; Г) 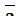 .
.
1.4 Розв'яжіть рівняння 2 - 4(х - 1) = 2(х + 3).
А)-2; Б)0; В)-6; Г) 2.
1.5 Чому дорівнює добуток коренів квадратного рівняння х2 - 7х - 6 = 0?
А) 6; Б) 7; В) -7; Г) - 6.
1.6 Обчисліть значення виразу (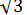 - 2)2 +
- 2)2 +  .
.
А)7 +  ; Б) -1 +
; Б) -1 +  ; В) 7; Г) -1.
; В) 7; Г) -1.
1.7 Для якої нерівності число 1 є розв'язком?
А) 3x2 + 6x  0; В) -х2 + 2х - 2 > 0;
0; В) -х2 + 2х - 2 > 0;
Б) х2 - 4х + 4  0; Г) -3х2 - 6х
0; Г) -3х2 - 6х  0.
0.
 1.8 На рисунку зображено графік руху туриста.
1.8 На рисунку зображено графік руху туриста.
Скільки часу тривав привал?
А) 1 год; В)2,5год;
Б) 3,5 год; Г) 5 год
1.9 У якій точці розміщено центр кола, вписаного в трикутник?
A)у точці перетину бісектрис трикутника;
Б) у точці перетину висот трикутника;
B)у точці перетину серединних перпендикулярів до сторін трикутника;
Г) у точці перетину медіан трикутника.
1.10 Промінь ОМ проходить між сторонами  AОВ - 56° так, що
AОВ - 56° так, що  AОМ на 18° менший від
AОМ на 18° менший від  МОВ. Знайдіть градусну міру
МОВ. Знайдіть градусну міру  AОМ і
AОМ і  МОВ.
МОВ.
А) 10° і 46°; Б) 19° і 37°; В) 47° і 29°; Г) 12° і 44°.
1.11 У трапеції діагоналі дорівнюють 8 см і 5  см, а кут між ними - 30°. Знайдіть площу трапеції.
см, а кут між ними - 30°. Знайдіть площу трапеції.
А)20  см2; Б) 60 см2; В) 30 см2; Г)10
см2; Б) 60 см2; В) 30 см2; Г)10  см2.
см2.
1.12 У рівнобедреному трикутнику основа дорівнює 12 см, а бічна сторона - 10 см. Знайдіть площу трикутника.
А) 96 см2; Б) 48 см2; В) 60 см2; Г) 120 см2.
Частина друга
Розв'яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
2.1 Спростіть вираз 
2.2 Обчисліть значення виразу  .
.
2.3 Розв'яжіть систему рівнянь 
2.4 У ∆АВС АС = 2 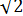 см, АВ = 2
см, АВ = 2  см,
см,  B = 45°. Знайдіть кут С.
B = 45°. Знайдіть кут С.
Частина третя
Розв'язання задач 3.1-3.3 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1 Через одну трубу можна наповнити басейн на 3 год швидше, ніж через другу спорожнити цей басейн. Якщо одночасно відкрити обидві труби, то басейн наповниться за 36 год. За скільки годин перша труба може наповнити, а друга - спорожнити басейн?
3.2 Побудуйте графік функції у = х2 - 4 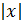 + 3. Використовуючи побудований графік, укажіть найменше значення функції.
+ 3. Використовуючи побудований графік, укажіть найменше значення функції.
3.3 Доведіть, що чотирикутник АВСDз вершинами в точках А(0; 6), B(5; 7), С(4; 2) і D(-1; 1) є ромбом.
Варіант №18
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на Вашу думку, відповідь і позначте її у бланку відповідей.
1.1 Знайдіть корінь рівняння 2х - 17 = 53.
А) 18; Б) 72; В) 35; Г)40.
1.2 Скільки кілограмів сушених грибів отримають з 18 кг свіжих, якщо з 12 кг свіжих грибів отримали 1,8 кг сушених?
А) 0,9 кг; Б) 5,4 кг; В) 3,6 кг; Г) 2,7 кг
1.3 Знайдіть розв'язок системи рівнянь 
А) (4;-2); Б) (2;-4); В) (-4; 2); Г)(-2;4).
1.4 Яке з рівнянь є лінійним?
А)х2=7х; Б)-5x =  ; В)х + 7 = х2; Г)
; В)х + 7 = х2; Г)  7 = 4.
7 = 4.
1.5 Виконайте множення 
A)6x2y4; Б)  B)6 x3y3; Г)
B)6 x3y3; Г)  .
.
1.6 Обчисліть значення виразу 80·2-3-22.
А) 40; Б) 636; В) 14; Г) 6.
1.7 Розв'яжіть нерівність х2 < 49.
А) (-∞; 7]; Б) (-∞; 7] U [7;+∞); В) (-∞; -7]; Г) [-7; 7].
1.8 Знайдіть різницю арифметичної прогресії 8; 3; -2; -7;...
А) 5; Б)-5; В) 8; Г) 3.
1.9 Який з чотирикутників завжди має рівні діагоналі?
А) паралелограм; В) ромб;
Б) прямокутник; Г) трапеція.
1.10 Знайдіть середню лінію рівнобічної трапеції, якщо її бічна сторона дорівнює 6 см, а периметр - 48 см.
А) 36 см; Б) 18 см; В) 16 см; Г)19см.
1.11 Радіус кола дорівнює 2  см. Знайдіть сторону правильного трикутника, описаного навколо цього кола.
см. Знайдіть сторону правильного трикутника, описаного навколо цього кола.
А) 12 см; Б) 6 см; В)6  см; Г)3
см; Г)3  см.
см.
1.12 Знайдіть площу кругового сектора радіуса 5 см, центральний кут якого дорівнює 72°.
А)10 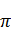 см2; Б)20
см2; Б)20 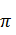 см2; В)
см2; В) 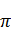 см2; Г)5
см2; Г)5 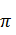 см2.
см2.
Частина друга
Розв'яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
2.1 Спростіть вираз  , якщо а < 0.
, якщо а < 0.
2.2 Знайдіть точки параболи, що є графіком функції у = х2 - 2х - 4, у яких абсциси й ординати рівні між собою.
2.3 Знайдіть суму нескінченної геометричної прогресії (bп),якщо
b 3 = 5, q =  .
.
2.4 У ∆АВС  C = 90°, tg В =
C = 90°, tg В =  , АВ=26 см. Знайдіть довжину меншого катета трикутника.
, АВ=26 см. Знайдіть довжину меншого катета трикутника.
Частина третя
Розв'язання задач 3.1-3.3 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1 Катер проплив 22 км за течією річки і 36 км проти течії за час, потрібний для того, щоб проплисти 6 км на плоту. Знайдіть швидкість течії, якщо власна швидкість катера дорівнює 20 км/год.
3.2 Складіть квадратне рівняння, корені якого на три більші за відповідні корені рівняння х2 - 2х - 7 = 0
3.3 Сторони трикутника дорівнюють 3 см і 5 см, а кут між ними 120°. Знайдіть площу подібного йому трикутника, периметр якого дорівнює 30 см.
Варіант №19
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на Вашу думку, відповідь і позначте її у бланку відповідей.
1.1 Яку частину круга на рисунку заштриховано?

1.2 Яка з числових нерівностей є правильною?
А) -37,5 > 3,5; В) -5000 > -400;
Б)-475 < -375; Г)0 < -20,7.
1.3 Яка пара чисел є розв’язком системи  ?
?
А)(2;1); Б)(-1;-2); В)(-1;2); Г)(1;2).
1.4 Знайдіть точку перетину графіка функції у = 5х - 20 з віссю абсцис.
А)(0;4); Б) (0;-20); В)(4;0); Г) (-4; 0).
1.5 Виконайте ділення 
А)  ; Б)
; Б)  ; В)
; В)  ; Г)
; Г) 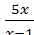 .
.
1.6 Знайдіть значення виразу 30 + 3 -4 · (3 -2) -3 - (0,5) -2.
А) 5; Б) 14; В) 6; Г) 10,25
1.7 Розв'яжіть систему нерівностей  .
.
А)(-6;-3); Б)(-∞; 2); В)(-6; -3]; Г)(-∞: -6).
1.8 Знайдіть порядковий номер члена an арифметичної прогресії, якщо а1= 5, d = 3, ап = 29.
А) 8; Б) 9; В) 7; Г) 10.
1.9 Яка градусна міра кута, якщо суміжний з ним кут дорівнює 110°?
А) 10°; Б) 110°; В) 70°; Г)90°.
1.10 Знайдіть міру вписаного кута, який спирається на дугу, що становить
 кола.
кола.
А) 60°; Б) 15°; В) 30°; Г) 120°.
1.11 Запишіть рівняння кола з центром у точці O(-2; 1) та радіусом, що дорівнює 4.
А) (х - 2)2 + (у+ 1)2 = 16; В) (х + 2)2 + (у - 1)2 = 16;
Б) (х + 2)2 + (у- 1)2 = 4; Г) (х - 2)2 + (у - 1)2 = 16.
1.12 У ∆АВС знайдіть міру кута В, якщо АВ =  см, АС =
см, АС =  см,
см,  С = 60°.
С = 60°.
А) 75°; Б) 45°; В) 135°; Г)65°.
Частина друга
Розв'яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
2.1 Обчисліть  .
.
2.2 Задайте формулою лінійну функцію, графік якої проходить через точки (1; -5) і (-3; -13).
2.3 Вкладник поклав до банку 10 000 гривень під 16 % річних. Скільки відсоткових грошей матиме вкладник через два роки?
2.4 Сторони чотирикутника відносяться як 2: 3: 3: 4. Знайдіть периметр подібного йому чотирикутника, найбільша сторона якого дорівнює 20 см.
Частина третя
Розв'язання задач 3.1-3.3 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1 З міста А в місто В виїхав велосипедист. Через 3 год у тому самому напрямі з міста А виїхав мотоцикліст і прибув у місто В одночасно з велосипедистом. Знайдіть швидкість велосипедиста, якщо вона менша за швидкість мотоцикліста на 45 км/год, а відстань між містами дорівнює 60 км.
3.2 Побудуйте графік функції y=  .
.
3.3 Знайдіть площу трапеції, основи якої дорівнюють 10 см і 14 см, а бічні сторони - 13 см і 15 см.
Варіант №20
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на Вашу думку, відповідь і позначте її у бланку відповідей.
1.1 З поля площею 6,4 га зібрали 320 ц зерна. Який урожай зерна зібрали в середньому з кожного гектара?
А) 50 ц; Б) 20 ц; В) 25 ц; Г) 64 ц.
1.2 Чому дорівнює найменше спільне кратне чисел 12 і 16?
А) 48; Б) 2; В) 96; Г)4.
1.3 Спростіть вираз7х - (2а - х).
А) 6x - 2а; Б)8х - 2а; В)6х+2а; Г) 6ха.
1.4 Розкладіть на множники вираз 3m + mk - 3n - kn.
А) (3 + k)(m - п); В) (m + n)(3 - k);
Б) m (3 + k) - n (3 - k); Г) (m - n)(3 - k).
1.5 Подайте у вигляді квадрата двочлена вираз 9а2 - 6аb + b2.
А)(3а + b)2; Б)(9а + b)2; В) (3а - b)(3а + b); Г) (3а-b)2.
1.6 Виконайте додавання  .
.
А)  ; Б)
; Б)  ; В)
; В) 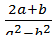 ; Г)
; Г)  .
.
1.7 Оцініть значення виразу х + 3, якщо 2 < х < 7.
А)2< x+3 <7; В) 5< х + 3 <10;
Б)2> х + 3 >7; Г) 5< х <10.
1.8 Вкладник поклав до банку 1500 грн. Під який відсоток річних покладено гроші, якщо через рік на рахунку вкладника було 1725 грн.?
А) 115%; Б) 85%; В) 15%; Г) 25 %.

1.9 На рисунку зображено паралельні прямі а і b, які перетинає січна с. Користуючись рисунком, знайдіть  1, якщо
1, якщо  2 = 50°.
2 = 50°.
А) 50°; Б) 140°; В) 40°; Г) 130°.
 1.10. У прямокутному трикутнику з кутом
1.10. У прямокутному трикутнику з кутом  та катетами 6 см і 7 см знайдіть cos
та катетами 6 см і 7 см знайдіть cos  (див. рис).
(див. рис).
А)  ; Б)
; Б)  ; В)
; В)  ; Г)
; Г)  .
.
1.11 Обчисліть скалярний добуток векторів  (6; - 5) і
(6; - 5) і 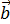 (3;4).
(3;4).
А) 38; Б) 2; В)-2; Г)  .
.
1.12 При якому значенні х вектори  (3; 9) та
(3; 9) та  (3; х) перпендикулярні?
(3; х) перпендикулярні?
А)1; Б) 9; В)-1; Г) 3.
Частина друга
Розв'яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
2.1 Розв'яжіть рівняння (х2 + х)2 + 2(х2 + х) - 8 = 0.
2.2 Складіть квадратне рівняння з цілими коефіцієнтами, корені якого дорівнюють числам 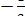 і 5.
і 5.
2.3 При яких значеннях р і q графік функції у = х2 +рх + q проходить через точки (1; -2) і (-4; 3)?
2.4 Знайдіть на осі абсцис точку, рівновіддалену від точок A(1; 5) i В(3; 1).
Частина третя
Розв'язання задач 3.1-3.3 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1 Автомобіль мав проїхати 1200 км із певною запланованою швидкістю. Після того як він проїхав третину шляху із цією швидкістю, автомобіль витратив на зупинку 2 год. Збільшивши швидкість на 20 км/год, автомобіль прибув у пункт призначення вчасно. Якою була швидкість автомобіля до зупинки?
3.2 Доведіть, що значення виразу

є додатним при всіх допустимих значеннях змінної.
3.3. Бісектриса гострого кута паралелограма ділить його сторону у відношенні 3: 4, рахуючи від вершини тупого кута. Периметр паралелограма дорівнює 80 см. Знайдіть довжини його сторін.
Атестаційний бланк
для державної підсумкової атестації
з математики учня (учениці)______ класу
загальноосвітньої школи І-ІІІ ступенів №9
__________________________________________________
П.І.Б.
Варіант №_____
Перша частина
| № завдання | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 1.10 | 1.11 | 1.12 |
| Набрані бали |
Загальна кількість набраних балів______
Друга частина
| № завдання | 2.1 | 2.2 | 2.3 | 2.4 |
Загальна кількість набраних балів________
Третя частина
Загальна кількість набраних балів______
Оцінка досягнень учня (учениці)(всього балів)______________
Підписи:
Голова комісії: Члени комісії:
_______ ________________ ________ _________________
________ _________________
Вчитель:
________ ________________
РОБОТА
на державну підсумкову атестацію
З математики
за курс основної школи
учня (учениці)_________ класу
загальноосвітньої школи І-ІІІ ступенів №9
__________________________________________________________
(Прізвище, ім’я, по-батькові у родовому відмінку)
Варіант___________
 Завдання 1.1 – 1.12 правильну відповідь позначте тільки так:
Завдання 1.1 – 1.12 правильну відповідь позначте тільки так:
А Б В Г А Б В Г А Б В Г


 1.1 1.5 1.9
1.1 1.5 1.9
1.2 1.6 1.10
1.3 1.7 1.11
1.4 1.8 1.12
У завданнях 2.1 – 2.4 упишіть відповідь.
| 2.1 | |
| 2.2 |
| 2.3 | |
| 2.4 |
Щоб виправити відповідь до завдань, запишіть його номер у спеціально відведеній клітинці, а правильну, на вашу думку, відповідь – у відповідному місці.
Завдання 1.1 – 1.12
А Б В Г

 1.
1.
1.
1.
1.
Завдання 2.1 – 2.4.
| Номер завдання | Виправлена відповідь |
 2. 2.
| |
 2. 2.
|
Не нашли, что искали? Воспользуйтесь поиском: