
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Отображение трехмерных графиков
Программа MatLab обладает рядом инструментов для визуализации графиков в трехмерном пространстве. Такие задачи обычно возникают при отображении графиков функций типа  .
.
В самом простом случае, для визуализации графика в трехмерных координатных осях, используется функция
plot3(X,Y,Z);
которая в качестве первых двух аргументов принимает матрицы с координатами точек по осям Ox и Oy соответственно, а в качестве третьего аргумента передается матрица значений точек по оси Oz. Рассмотрим работу данной функции на примере отображения графика функции
 ,
,
при  и
и  .
.
Сформируем матрицы X и Y, содержащие координаты точек данного графика по осям Ox и Oy соответственно. Данные матрицы нужны для того, чтобы функция plot3() «знала» какие реальные координаты соответствуют точке Z(i,j) матрицы значений по оси Oz. Для этого достаточно взять i-ю и j-ю компоненту матриц

Формирование матриц X и Y можно осуществить с помощью функции
[X,Y]=meshgrid(x,y);
языка MatLab. Здесь x и y – одномерные векторы значений координат по осям Ox и Oy соответственно, которые можно сформировать как
x=-1:0.1:1; % координаты точек по оси Ox
y=-2:0.1:2; % координаты точек по оси Oy
и, затем, вычислить матрицы
[X,Y]=meshgrid(x,y); % матрицы координат точек по осям Ox и Oy
В результате, матрицы X и Y будут содержать следующие первые восемь значений по строкам и столбцам:
Матрица X:
-1 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3
-1 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3
-1 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3
-1 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3
-1 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3
-1 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3
-1 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3
-1 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3
Матрица Y:
-2 -2 -2 -2 -2 -2 -2 -2
-1,9 -1,9 -1,9 -1,9 -1,9 -1,9 -1,9 -1,9
-1,8 -1,8 -1,8 -1,8 -1,8 -1,8 -1,8 -1,8
-1,7 -1,7 -1,7 -1,7 -1,7 -1,7 -1,7 -1,7
-1,6 -1,6 -1,6 -1,6 -1,6 -1,6 -1,6 -1,6
-1,5 -1,5 -1,5 -1,5 -1,5 -1,5 -1,5 -1,5
-1,4 -1,4 -1,4 -1,4 -1,4 -1,4 -1,4 -1,4
-1,3 -1,3 -1,3 -1,3 -1,3 -1,3 -1,3 -1,3
Используя данные матрицы, можно вычислить значения матрицы Z, следующим образом:
Z=exp(-X.^2-Y.^2);
и отобразить результат на экране
plot3(X,Y,Z);

Рис. 3.10. Пример отображения графика с помощью функции plot3()
Из приведенного рисунка видно, что функция plot3() отображает график в виде набора линий, каждая из которых соответствует сечению графика функции  вдоль оси Oy.
вдоль оси Oy.
Такое представление графика не всегда удобно, т.к. набор одномерных не дает полное представление о характере двумерной плоскости. Более лучшей визуализации можно получить, используя функцию
mesh(X,Y,Z); % отображение графика в виде сетки
В результате получим следующий вид трехмерного графика (рис. 3.11).
Благодаря использованию функции mesh() получается график, образованный интерполяцией точек массивов X, Y и Z линиями по осям Ox и Oy. Кроме того, цветом указывается уровень точки по оси Oz: от самого малого значения (синего) до самого большого (красного) и производится удаление «невидимых» линий. Это позволяет лучше визуально оценивать структуру трехмерного графика по сравнению с функцией plot3(). Если же необходимо отобразить «прозрачный» график, то следует выключить режим удаления «невидимых» линий:
hidden off; % скрытые линии рисуются
В системе MatLab предусмотрена функция визуализации непрерывной поверхности в трехмерных осях
surf(X,Y,Z); % отображение непрерывной поверхности
В результате получается график, представленный на рис. 3.12.

Рис. 3.11. Результат работы функции mesh()

Рис. 3.12. Результат работы функции surf()
Функция surf() может использоваться в режиме
shading interp; % интерполяция тени на гранях графика
которая интерполирует цвет на гранях для получения более гладкого изображения поверхности (рис. 3.13). Также существует возможность менять цветовую карту отображения графика с помощью функции
colormap(<карта>); % установка цветовой карты
Например, карта с именем hot, используемая по умолчанию может быть заменена на любую другую доступную (hot, hsv, gray, pink, cool, bone copper) или созданную самостоятельно.
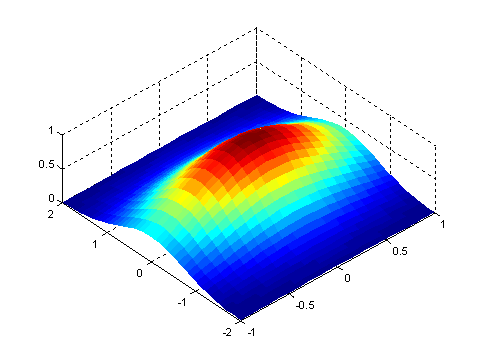
Рис. 3.13. Результат работы функции surf() в режиме shading interp
Следует отметить, что все три функции plot3(), mesh() и surf() могут быть использованы и с одним аргументом Z, который интерпретируется как матрица со значениями точек по оси Oz.
Для масштабирования отдельных участков трехмерных графиков, также как и в случае с двумерными графиками, используется функция
axis([xmin xmax ymin ymax zmin zmax]);
с очевидным набором параметров.
Для оформления трехмерных графиков можно пользоваться описанными ранее функциями: text, xlabel, ylabel, zlabel, title, grid [on/off], subplot.
Наконец, для трёхмерных графиков существует возможность изменять точку их обзора, т.е. положение виртуальной камеры с помощью функции
view([az el]);
где az – угол азимута; el – угол возвышения. Изменение первого угла означает вращение плоскости xOy вокруг оси Oz против часовой стрелки. Угол возвышения есть угол между направлением на камеру и плоскостью xOy.
Не нашли, что искали? Воспользуйтесь поиском: