Глава 3. Работа с графиками в MatLab

MatLab предоставляет богатый инструментарий по визуализации данных. Используя внутренний язык, можно выводить двумерные и трехмерные графики в декартовых и полярных координатах, выполнять отображение изображений с разной глубиной цвета и разными цветовыми картами, создавать простую анимацию результатов моделирования в процессе вычислений и многое другое.

Функция plot

Рассмотрение возможностей MatLab по визуализации данных начнем с двумерных графиков, которые обычно строятся с помощью функции plot(). Множество вариантов работы данной функции лучше всего рассмотреть на конкретных примерах.

Предположим, что требуется вывести график функции синуса в диапазоне от 0 до . Для этого зададим вектор (множество) точек по оси Ox, в которых будут отображаться значения функции синуса:

x = 0:0.01:pi;

В результате получится вектор столбец со множеством значений от 0 до и с шагом 0,01. Затем, вычислим множество значений функции синуса в этих точках:

y = sin(x);

и выведем результат на экран

plot(x,y);

В результате получим график, представленный на рис. 3.1.

Представленная запись функции plot() показывает, что сначала записывается аргумент со множеством точек оси Ох, а затем, аргумент со множеством точек оси Oy. Зная эти значения, функция plot() имеет возможность построить точки на плоскости и линейно их интерполировать для придания непрерывного вида графика.

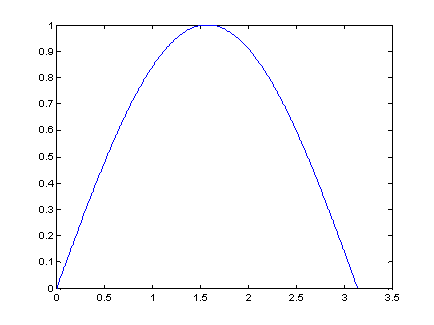
Рис. 3.1. Отображение функции синуса с помощью функции plot().

Функцию plot() можно записать и с одним аргументом x или y:

plot(x);
plot(y);

в результате получим два разных графика, представленные на рис. 3.2.

Анализ рис. 3.2 показывает, что в случае одного аргумента функция plot() отображает множество точек по оси Oy, а по оси Оx происходит автоматическая генерация множества точек с единичным шагом. Следовательно, для простой визуализации вектора в виде двумерного графика достаточно воспользоваться функцией plot() с одним аргументом.

Для построения нескольких графиков в одних и тех же координатных осях, функция plot() записывается следующим образом:

x = 0:0.01:pi;
y1 = sin(x);
y2 = cos(x);
plot(x,y1,x,y2);

Результат работы данного фрагмента программы представлен на рис. 3.3.

а) б)

Рис. 3.2. Результаты работы функции plot() с одним аргументом:

а – plot(x); б – plot(y).

Рис. 3.3. Отображение двух графиков в одних координатных осях.

Аналогичным образом можно построить два графика, используя один аргумент функции plot(). Предположим, что есть два вектора значений

y1 = sin(x);
y2 = cos(x);

которые требуется отобразить на экране. Для этого объединим их в двумерную матрицу

в которой столбцы составлены из векторов y1 и y2 соответственно. Такая матрица будет отображена функцией

plot([y1’ y2’]); % апострофы переводят вектор-строку
% в вектор-столбец

в виде двух графиков (рис. 3.4).

Рис. 3.4. Отображение двумерной матрицы в виде двух графиков.

Два вектора в одних осях можно отобразить только в том случае, если их размерности совпадают. Когда же выполняется работа с векторами разных размерностей, то они либо должны быть приведены друг к другу по числу элементов, либо отображены на разных графиках. Отобразить графики в разных координатных осях можно несколькими способами. В самом простом случае можно создать два графических окна и в них отобразить нужные графики. Это делается следующим образом:

x1 = 0:0.01:2*pi;
y1 = sin(x1);

x2 = 0:0.01:pi;
y2 = cos(x2);

plot(x1, y1); % рисование первого графика
figure; % создание 2-го графического окна
plot(x2, y2); % рисование 2-го графика во 2-м окне

Функция figure, используемая в данной программе, создает новое графическое окно и делает его активным. Функция plot(), вызываемая сразу после функции figure, отобразит график в текущем активном графическом окне. В результате на экране будут показаны два окна с двумя графиками.

Неудобство работы приведенного фрагмента программы заключается в том, что повторный вызов функции figure отобразит на экране еще одно новое окно и если программа будет выполнена дважды, то на экране окажется три графических окна, но только в двух из них будут актуальные данные. В этом случае было бы лучше построить программу так, чтобы на экране всегда отображалось два окна с нужными графиками. Этого можно достичь, если при вызове функции figure в качестве аргумента указывать номер графического окна, которое необходимо создать или сделать активным, если оно уже создано. Таким образом, вышеприведенную программу можно записать так.

x1 = 0:0.01:2*pi;
y1 = sin(x1);

x2 = 0:0.01:pi;
y2 = cos(x2);

figure(1); %создание окна с номером 1
plot(x1, y1); % рисование первого графика
figure(2); % создание графического окна с номером 2
plot(x2, y2); % рисование 2-го графика во 2-м окне

При выполнении данной программы на экране всегда будут отображены только два графических окна с номерами 1 и 2, и в них показаны графики функций синуса и косинуса соответственно.

В некоторых случаях большего удобства представления информации можно достичь, отображая два графика в одном графическом окне. Это достигается путем использования функции subplot(), имеющая следующий синтаксис:

subplot(<число строк>, <число столбцов>, <номер координатной оси>)

Рассмотрим пример отображения двух графиков друг под другом вышеприведенных функций синуса и косинуса.

x1 = 0:0.01:2*pi;
y1 = sin(x1);

x2 = 0:0.01:pi;
y2 = cos(x2);

figure(1);
subplot(2,1,1); % делим окно на 2 строки и один столбец
plot(x1,y1); % отображение первого графика
subplot(2,1,2); % строим 2-ю координатную ось
plot(x2,y2); % отображаем 2-й график в новых осях

Результат работы программы показан на рис. 3.5.

Аналогичным образом можно выводить два и более графиков в столбец, в виде таблицы и т.п. Кроме того, можно указывать точные координаты расположения графика в графическом окне. Для этого используется параметр position в функции subplot():

subplot(‘position’, [left bottom width height]);

где left – смещение от левой стороны окна; bottom – смещение от нижней стороны окна; width, height – ширина и высота графика в окне. Все эти переменные изменяются в пределах от 0 до 1.

Рис. 3.5. Пример работы функции subplot.

Ниже представлен фрагмент программы отображения графика функции синуса в центре графического окна. Результат работы показан на рис. 3.6.

x1 = 0:0.01:2*pi;
y1 = sin(x1);

subplot(‘position’, [0.33 0.33 0.33 0.33]);
plot(x1,y1);

В данном примере функция subplot() смещает график на треть от левой и нижней границ окна и рисует график с шириной и высотой в треть графического окна. В результате, получается эффект рисования функции синуса по центру основного окна.

Таким образом, используя параметр position можно произвольно размещать графические элементы в плоскости окна.

Рис. 3.6. Пример работы функции subplot с параметром position.

Не нашли, что искали? Воспользуйтесь поиском: