Тригонометрические уравнения

Простейшие тригонометрические уравнения.

1. sinx = a, |a| 1, x = (–1) k arcsin a + k, k

Частные случаи:

sinx = –1	sin x = 0	sin x = 1
x = – + 2 k, k	x = k, k	x = + 2 k, k
	| a| >1 корней нет

2. cos x = a, |a| 1

x = ± arccos a + 2 k, k

Частные случаи:

cos x = –1	cos x = 0	cos x = 1
x = + 2 k, k	x = + k, k	x = 2 k, k
	|a| >1 корней нет

3. tg x = a, a
x = ± arctg a + k, k

Основные типы тригонометрических уравнений.

1. Уравнения, сводящиеся к простейшим.

2. Уравнения, сводящиеся к квадратным.

3. Уравнения, решаемые разложением на множители.

4. Однородные уравнения: asinx + bcosx = 0, a sin 2 x + b sinxcosx + c cos 2 x = 0.

Примеры.

1. Уравнения, сводящиеся к простейшим.

1) Решить уравнение

Решение:

Ответ:

2) Найти корни уравнения

(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку [0; 2 ].

Решение:

Ответ:

2. Уравнения, сводящиеся к квадратным.

1) Решить уравнение 2 sin 2 x – cosx –1 = 0.

Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем

Ответ:

2) Решить уравнение cos 2x = 1 + 4 cosx.

Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем

Ответ:

.

3) Решить уравнение tgx – 2ctgx + 1 = 0

Решение:

Ответ:

.

3. Однородные уравнения

1) Решить уравнение 2sinx – 3cosx = 0

Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим

Ответ:

.

2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x

Решение:

Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим

sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0

Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получим

tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y1= 4; y2= 2
а) tgx = 4, x= arctg4 + 2 k, k
б) tgx = 2, x= arctg2 + 2 k, k .

Ответ: arctg4 + 2 k, arctg2 + 2 k, k

4. Уравнения вида a sinx + b cosx = с, с ≠ 0.

1) Решить уравнение .

Решение:

Ответ:

.

4. Уравнения, решаемые разложением на множители.

1) Решить уравнение sin2x – sinx = 0.

Решение: Используя формулу sin2x = 2sinxcosx, получим

2sinxcosx – sinx = 0,

sinx (2cosx – 1) = 0.

Произведение равно нулю, если хотя бы один из множителей равен нулю.

Ответ:

.

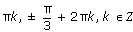2) Решить уравнение sin2x – sinx = 2cosx – 1

Решение: Применим формулу sin2x = 2sinxcosx, получим

2sinxcosx – sinx = 2cosx – 1

sinx (2cosx – 1) = 2cosx – 1

sinx (2cosx – 1) – (2cosx – 1) = 0

(2cosx – 1) (sinx –1) = 0

Произведение равно нулю, если хотя бы один из множителей равен нулю.

Ответ:

.

Не нашли, что искали? Воспользуйтесь поиском: