
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Ортогональная регрессия
При коэффициенте корреляции, приближающемся к единице, расчеты по уравнениям прямой и обратной регрессии дают достаточно близкие результаты. Чем меньше по абсолютной величине коэффициент корреляции, тем больше угол между линиями прямой и обратной регрессии и выше различие между результатами, полученными по двум уравнениям. При этом искажается физический смысл полученных зависимостей. Целесообразно иметь одно уравнение, описывающее взаимозависимость между исследуемыми величинами.
Ортогональная регрессия дает одно уравнение на основе уравнений прямой и обратной регрессии. Линия ортогональной регрессии должна быть биссектрисой - делить пополам угол между линиями прямой и обратной регрессии.
1. Определяем углы наклона линий регрессии к осям координат
b1(yх) = tg α = 0,5326, угол α = 27,920; b1(xy) = tg β = 1,4294, угол β = 55,0350;
где b1(yх) – угловой коэффициент уравнения прямой регрессии - тангенс угла наклона линии прямой регрессии к оси абсцисс, b1(xy) - угловой коэффициент уравнения обратной регрессии - тангенс угла наклона линии обратной регрессии к оси ординат.
ВАРИАНТЫ ЗАДАНИЙ
Исходные данные для контрольной работы выбирают из таблицы 1. В верхней строке приведены координаты точек по оси абсцисс (Х) от -6 до 13. В следующих строках – координаты точек по оси ординат (У). Для статистической обработки надо выбрать 10 точек.
Номер варианта контрольной работы определяется по номеру студента в списке группы. Возможно изменение темы контрольной работы по согласованию с преподавателем данной дисциплины.
Например, для 1-го варианта: Х1 = -5, У1 = 1; Х2 = -3, У2 = 2; Х3 = -1, У3 = 4; Х4 = 1, У4 = 3; Х5 = 3, У5 = 5; Х6 = 5, У6 = 4; Х7 = 7, У7 = 6; Х8 = 9, У8 = 5; Х9 = 11, У9 = 7; Х10 = 13, У10 = 7.
Таблица 1
Исходные данные
| № варианта | Верхняя строка – ось абсцисс – х, далее строки – ось ординат - у | ||||||||||||||||||||
| -6 | -5 | -4 | -3 | -2 | -1 | ||||||||||||||||
| -3 | -3 | -5 | |||||||||||||||||||
| -4 | -4 | -6 | |||||||||||||||||||
| -12 | -10 | -7 | -8 | -5 | -1 | ||||||||||||||||
| -12 | -10 | -7 | -8 | -5 | -1 | ||||||||||||||||
| -1 | -2 | -3 | -2 | -4 | -5 | ||||||||||||||||
| -1 | -2 | -1 | -3 | -4 | |||||||||||||||||
Продолжение табл.1.
| № варианта | Верхняя строка – ось абсцисс – х, далее строки – ось ординат - у | |||||||||||||||||||
| -6 | -5 | -4 | -3 | -2 | -1 | |||||||||||||||
| -1 | -4 | -6 | ||||||||||||||||||
| -2 | -5 | -7 | ||||||||||||||||||
| -1 | -2 | -4 | -4 | -6 | -7 | |||||||||||||||
| -6 | -5 | -5 | -4 | -3 | -3 | -2 | -1 | |||||||||||||
| -6 | -5 | -4 | -4 | -3 | -2 | -2 | -1 | |||||||||||||
| -6 | -6 | -5 | -5 | -5 | -4 | -4 | -4 | -3 | -3 | |||||||||||
| -3 | -2 | -2 | -2 | -1 | -1 | |||||||||||||||
| -14 | -12 | -11 | -10 | -9 | -8 | -6 | -5 | -4 | -3 | |||||||||||
| -13 | -12 | -11 | -9 | -8 | -7 | -6 | -4 | -3 | -2 | |||||||||||
| -14 | -13 | -12 | -12 | -11 | -11 | -10 | -9 | -9 | -8 | |||||||||||
| -8 | -7 | -6 | -6 | -5 | -4 | -4 | -3 | -3 | -2 |
2. Выполняем вычисления аналогичные прямой регрессии. Коэффициенты уравнения обратной регрессии статистически значимы. Получили уравнение обратной регрессии
X = b0 (ху) + b1 (ху) У = -3,55 + 1,43 У.
X1р = -3,55 + 1,43 х5,0 = 3,6;
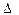 X1 = 1,5 – 3,6 = - 2,1;
X1 = 1,5 – 3,6 = - 2,1; 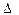 X12 = 4,41;
X12 = 4,41;
X2р = -3,55 + 1,43 х4,5 = 2,855 и т.д.;
3. Наносим линию обратной регрессии на график (рис. 2), указываем на графике величины коэффициентов обратной регрессии. Линия обратной регрессии круче линии прямой регрессии, обе линии пересекаются в центре массива экспериментальных данных  = 7,44 и
= 7,44 и 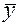 = 7,69.
= 7,69.
Корреляция
1. Вычисляем коэффициент парной корреляции
 =
=

Проверка r = Qху / (Qх Qу)0,5 = 52,84/(99,22х36,97)0,5 = 0,87.
2. Проверяем правильность вычислений по коэффициенту детерминации и произведению угловых коэффициентов регрессии.
r2 = b1 (ух) b1 (ху) = 0,53х1,43 = 0,76; r = 0,760,5 = 0,87.
Коэффициент детерминации r2 = 0,76 ( 76%) показывает процент разброса - изменчивости искомой величины Y относительно среднего значения, определяемого изменчивостью фактора Х.
Если выполняется условие 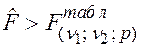 , то уравнение регрессии статистически значимо описывает результаты эксперимента.
, то уравнение регрессии статистически значимо описывает результаты эксперимента.
Для рассмотренного случая при 5%-ном уровне значимости уравнение неадекватно описывает результаты опытов. При 10%-ном уровне значимости табличное значения критерия Фишера составит 3,0145. В этом случае условие 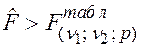 , 3,59 > 3,0145 выполняется.
, 3,59 > 3,0145 выполняется.
Уравнение прямой регрессии адекватно описывает результаты опытов при 10%-ном уровне значимости.
Обратная регрессия
1. Вычисляем коэффициенты уравнения линии обратной регрессии:
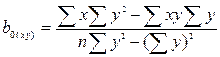 =
=
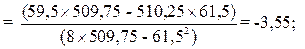
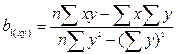 =
=
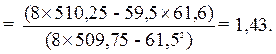
Проверка: b1 (ху) = Qху / Qу = 52,84/36,97 = 1,43;
b0 (ху) =  - b1 (ху)
- b1 (ху) 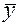 = 7,44 – 1,43х7,69 = -3,55.
= 7,44 – 1,43х7,69 = -3,55.
ПАРНЫЙ ЛИНЕЙНЫЙ
Не нашли, что искали? Воспользуйтесь поиском: