
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Метод наименьших квадратов. Например,имеем 8 пар измерений из предыдущих примеров (см
Например, имеем 8 пар измерений из предыдущих примеров (см. табл.2).
Х: 1,5; 4,0; 5,0; 7,0; 8,5; 10,0; 11,0; 12,5.
Y:5,0; 4,5; 7,0; 6,5; 9,5; 9,0; 11,0; 9,0.
1. Определяем расчетные значения и заполняем таблицу 2:
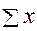 = 1,5+4,0+5,0+7,0+8,5+10,0+11,0+12,5 = 59,5;
= 1,5+4,0+5,0+7,0+8,5+10,0+11,0+12,5 = 59,5;
 = 5,0+4,5+7,0+6,5+9,5+9,0+11,0+9,0 = 61,5;
= 5,0+4,5+7,0+6,5+9,5+9,0+11,0+9,0 = 61,5;
 = 2,25+16,0+25,0+49,0+72,25+100,0+121,0+156,25 = 541,75;
= 2,25+16,0+25,0+49,0+72,25+100,0+121,0+156,25 = 541,75;
 = 25,0+20,25+49,0+42,25+90,25+81,0+121,0+81,0 = 509,75;
= 25,0+20,25+49,0+42,25+90,25+81,0+121,0+81,0 = 509,75;
 = 7,5+18,0+35,0+45,5+80,75+90,0+121,0+112,5 = 510,25;
= 7,5+18,0+35,0+45,5+80,75+90,0+121,0+112,5 = 510,25;
 =42,25+72,25+144,0+182,25+324,0+361,0+484,0+
=42,25+72,25+144,0+182,25+324,0+361,0+484,0+
+462,25 = 2072,0.
2. Определяем центр массива экспериментальных данных (опорную точку) средние значения
 =
= 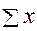 /n = 59,5/8 = 7,44 и
/n = 59,5/8 = 7,44 и 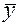 =
=  / n = 61,5/8 = 7,69.
/ n = 61,5/8 = 7,69.
3. Проверяем правильность вычислений
 .
.
2072,0 = 541,75+2×510,25+509,75 =2072,0.
3. 5,0 = b0 + 5,0 b1 ; 7. 11,0 = b0 + 11,0 b1 ;
4. 7,0 = b0 + 6,5 b1 ; 8. 12,5 = b0 + 9,0 b1 .
2. Суммируем результаты в каждом столбце, получаем разность значений от этих двух сумм и рассчитываем угловой коэффициент уравнения обратной регрессии b1(ху)
17,5 = 4,0 b0 + 23,0 b1 ; 42,0 = 4,0b0 + 38,5b1 ;
17,5 = 4,0 b0 + 23,0 b1 ;
24 ,5 = 15,5 b1 .
b1(ху) = 24,5/15,5 = 1,58; проверка 1,0/0,633 = 1,58.
6. Складываем результатысумм двух столбцов, получаемуравнениев которое подставляем b1(yх) = 1,58 и рассчитываем
b0 (ух)
59,5 = 8,0 b0 +61,5х1,58. 8,0 b0 = 59,5 - 61,5х1,58 = - 37,67;
b0 (ух) = - 37,67/8 = - 4,71;
7. Определяем расчетные значения Хр, абсолютные отклонения экспериментальных значений от расчетных ΔX, а также квадраты этих отклонений ΔX² и сводим их в таблицу 2:
Xр = - 4,71 + 1,58У.
X1р = - 4,71 + 1,58×5,0 = 3,19;
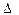 X1 = 1,5 – 3,19 = - 1,69;
X1 = 1,5 – 3,19 = - 1,69; 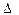 X12 = 2,3856;
X12 = 2,3856;
X2р = - 4,71 + 1,58×4,5 = 2,40;
-..- -..- -..- -..- -..- -..-
X8р = - 4,71 + 1,58×9,0 = 9,51.
8. Наносим линии прямой и обратной регрессии на рис.1 и обозначаем коэффициенты уравнений.
Продолжение табл.2.
МЕТОД СРЕДНИХ: 
| |||||||||
| yp | 3,93 | 5,5 | 6,13 | 7,39 | 8,34 | 9,28 | 9,91 | 10,86 | |
| Δy | 1,07 | -1,0 | 0,87 | -0,89 | 1,16 | -0,28 | 1,09 | -1,86 | ~0,0 |
| Δy² | 1,1449 | 1,00 | 0,7569 | 0,7921 | 1,3456 | 0,0784 | 1,1881 | 3,4596 | 9,7656 |
| xp | 3,19 | 2,4 | 6,35 | 5,56 | 10,3 | 9,51 | 12,67 | 9,51 | |
| Δx | -1,69 | 1,6 | -1,35 | 1,44 | -1,8 | 0,49 | -1,67 | 2,99 | ≈0,0 |
| Δx² | 2,8561 | 2,56 | 1,8225 | 2,0736 | 3,24 | 0,2401 | 2,7889 | 8,9401 | 24,52 |
МНК: 
| |||||||||
| x² | 2,25 | 16,0 | 25,0 | 49,0 | 72,25 | 100,0 | 121,0 | 156,25 | 541,75 |
| y² | 25,0 | 20,25 | 49,0 | 42,25 | 90,25 | 81,0 | 121,0 | 81,0 | 509,75 |
| xy | 7,5 | 18,0 | 35,0 | 45,5 | 80,75 | 90,0 | 121,0 | 112,5 | 510,25 |
| (x+y) | 6,5 | 8,5 | 12,0 | 13,5 | 18,0 | 19,0 | 22,0 | 21,5 | 121,0 |
| (x+y) ² | 42,25 | 72,25 | 144,0 | 182,25 | 324,0 | 361,0 | 484,0 | 462,25 | 2072,0 |
| yp | 4,53 | 5,85 | 6,38 | 7,44 | 8,24 | 9,03 | 9,56 | 10,35 | |
| Δy | 0,47 | -1,35 | 0,62 | -0,94 | 1,26 | -0,03 | 1,44 | -1,35 | ~0,0 |
| Δy² | 0,2209 | 1,8225 | 0,3844 | 0,8836 | 1,5876 | 0,0009 | 2,0736 | 1,8225 | 8,80 |
| xp | 3,6 | 2,855 | 6,46 | 5,745 | 10,035 | 9,32 | 12,18 | 9,32 | |
| Δx | -2,1 | 1,115 | -1,46 | 1,255 | -1,535 | 0,68 | -1,18 | 3,18 | ~0,0 |
| Δx² | 4,41 | 1,2432 | 2,1316 | 1,5750 | 2,3562 | 0,4624 | 1,3924 | 10,1124 | 23,68 |
ОРТОГОНАЛЬНАЯ РЕГРЕССИЯ: 
| |||||||||
| yp | 4,055 | 5,58 | 6,19 | 7,41 | 8,325 | 9,24 | 9,85 | 10,765 | |
| Δy | 0,945 | -1,08 | 0,81 | -0,91 | 1,175 | -0,24 | 1,15 | -1,765 | ~0,0 |
| Δy² | 0,8930 | 1,1664 | 0,6561 | 0,8281 | 1,3806 | 0,0576 | 1,3225 | 3,1152 | 9,42 |
| xp | 3,06 | 2,24 | 6,34 | 5,52 | 10,44 | 9,62 | 12,9 | 9,62 | |
| Δx | -1,56 | 1,76 | -1,34 | 1,48 | -1,94 | 0,38 | -1,9 | 2,88 | ~0,0 |
| Δx² | 2,4336 | 3,0976 | 1,7956 | 2,1904 | 3,7636 | 0,1444 | 3,61 | 8,2944 | 25,33 |
| Δh | 0,808 | -0,92 | 0,693 | -0,775 | 1,005 | -0,203 | 0,984 | -1,505 | ~0 |
| Δh² | 0,653 | 0,847 | 0,4805 | 0,600 | 1,010 | 0,0412 | 0,968 | 2,2647 | 6,86 |
Поскольку данный метод не является точным, то нецелесообразно полностью полагаться только на него.
Метод средних
Этот метод применяется для построения эмпирических зависимостей парного простейшего вида. Метод состоит в том, что параметры эмпирической формулы определяются из условия равенства нулю суммы всех отклонений наблюдаемой величины от среднего значения.
Вначале результаты наблюдений выравниваются (спрямляются, в контрольной работе данные уже линеаризированы), а затем для полученных новых переменных Х и У, связанных линейной зависимостью Ур = b0(yх) + b1(yх) Х, находят коэффициенты b0(yх) и b1(yх).
Для этого подставляют в уравнение полученные значения Х и У попарно, полученные равенства (условные уравнения) разбивают на две примерно равные группы. Группировка условных уравнений возможна несколькими способами, лучшим будет тот, который приводит к решению, дающему наименьшую сумму квадратов отклонений. Обычно уравнения группируют в последовательности опытных данных, разбивая их на равные или приблизительно равные части. Вообще равенства разбивают на столько групп, сколько коэффициентов уравнения предстоит определить.
Каждую группу уравнений почленно складывают. Получают систему из двух уравнений, из которых и находят коэффициенты, а затем переходят к натуральным переменным.
Например, имеем 8 пар измерений из предыдущего примера (см. табл.2).
Х: 1,5; 4,0; 5,0; 7,0; 8,5; 10,0; 11,0; 12,5.
Y:5,0; 4,5; 7,0; 6,5; 9,5; 9,0; 11,0; 9,0.
1. Составляем систему уравнений из двух групп для уравненияпрямой регрессия Y = b0 (ух)+ b1 (ух)X.
1. 5,0 = b0 +1,5 b1 ; 5. 9,5 = b0 + 8,5 b1 ;
2. 4,5 = b0 + 4,0 b1 ; 6. 9,0 = b0 + 10,0 b1 ;
3. 7,0 = b0 + 5,0 b1 ; 7. 11,0 = b0 + 11,0 b1 ;
4. 6,5 = b0 + 7,0 b1 ; 8. 9,0 = b0 + 12,5 b1 .
2. Суммируем результаты в каждом столбце, получаем разность значений от этих двух сумм и рассчитываем угловой коэффициент уравнения прямой регрессии b1(yх)
23,0 = 4,0 b0 + 17,5 b1 ; 38,5 = 4,0 b0 + 42,0b1 ;
23,0 = 4,0 b0 + 17,5 b1 ;
15,5 = 24,5 b1(yх) ;
b1(yх) = 15,5/24,5 = 0,633;
3. Складываем результатысумм двух столбцов, получаемуравнениев которое подставляем b1(yх) = 0,633 и рассчитываем b0 (ух)
61,5 = 8,0 b0 + 59,5х0,633; 8,0 b0 = 61,5 – 37,66 = 23,84;
b0 (ух) = 23,84/8 = 2,98;
4. Определяем расчетные значения YP, абсолютные отклонения экспериментальных значений от расчетных ΔY, а также квадраты этих отклонений ΔY² и сводим их в таблицу 2:
Ур = 2,98 + 0,63 X.
У1р = 2,98 + 0,63 × 1,5 = 3,93;
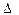 Y1 = У1 эк - У1 р = 5,0 – 3,93 = 1,07;
Y1 = У1 эк - У1 р = 5,0 – 3,93 = 1,07; 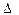 Y12 = 1,1449;
Y12 = 1,1449;
У2р = 2,98 + 0,63 х 4,0 = 5,50;
-..- -..- -..- -..- -..- -..-
У8 = 2,98 + 0,63 х 12,5 = 10,86.
5. Составляем систему уравнений из двух групп для уравненияобратной регрессия X = b0 (ху) + b1 (ху) У
1. 1,5 = b0 + 5,0 b1 ; 5. 8,5 = b0 + 9,5 b1 ;
2. 4,0 = b0 +4,5 b1 ; 6. 10,0 = b0 + 9,0 b1 ;
Не нашли, что искали? Воспользуйтесь поиском: