Простейшие задачи аналитической геометрии на плоскости.

Простейшие задачи аналитической геометрии

Расстояние между двумя точками

где и радиус-векторы точек и .

В координатах:

на прямой

на плоскости

в пространстве

Деление отрезка в данном отношении

В координатах:

на прямой ;

на плоскости , ;

в пространстве , ,

Линия на плоскости. Основные понятия.

Определение. Линия на плоскости – множество точек плоскости, обладающих некоторым только им присущим геометрическим свойством.

Определение. Уравнением линии на плоскости называется такое уравнение с двумя переменными, которому удовлетворяют координаты каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Определение. Уравнением линии в полярной системе координат называется уравнение , если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.

Линию на плоскости можно задать параметрическими уравнениями где и – непрерывны по параметру . Чтобы перейти от параметрических уравнений к уравнению вида надо из двух уравнений исключить параметр .

Пример. Какая линия определяется параметрическими уравнениями ?

Решение. Исключая параметр , приходим к уравнению . В силу параметрических уравнений , . Следовательно, данные параметрические уравнения определяют луч – биссектрису I-го координатного угла.

Линию на плоскости можно задать векторным уравнением , где – скалярный переменный параметр. Этому уравнению в системе координат соответствуют два скалярных уравнения .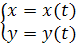

Векторное уравнение и параметрические уравнения линии имеют механический смысл: при перемещении точки на плоскости указанные уравнения называются уравнениями движения, а линия – траекторией точки, параметр при этом есть время.

Не нашли, что искали? Воспользуйтесь поиском: