Уравнение прямой в полярной системе координат. Нормальное уравнение прямой. Расстояние от данной точки до прямой.

Поло­жение прямой линии на плоскости будет вполне определено, если задать ее расстояние р от полюса О и угол а между полярной осью и осью I, проходящей через полюс пер­пендикулярно к прямой. Поло­жительным направлением оси I будем счи­тать направление от полюса к данной прямой (если прямая проходит через по­люс, то положительное направление оси / может быть выбрано произвольно). Очевидно, все точки данной прямой линии, и только они, обладают следую­щим свойством: проекция иа ось I отрезка ОМ_л проведенного из полюса О в точ­ку М прямой линии, равна р. Обозначая через rиῳ координаты произвольной точки прямой линии, указан­ное свойство мы можем записать в виде

rcos (ῳ — а)=р. Это и есть уравнение прямой линии в полярных координатах.

Нормальное уравнение прямой имеет вид

,

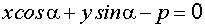где 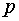– расстояние от прямой до начала координат; a – угол между нормалью к прямой и осью .

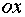Нормальное уравнение можно получить из общего уравнения (1), умножив его на нормирующий множитель 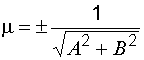, знак m противоположен знаку , чтобы .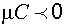

Косинусы углов между прямой и осями координат называют направляющими косинусами,a – угол между прямой и осью 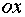, b – между прямой и осью :

,

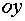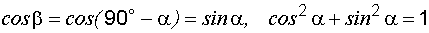тем самым, нормальное уравнение можно записать в виде

.

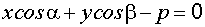Расстояние от точки 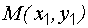до прямой определяется по формуле

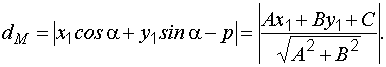
Расстоянием от точки M₁ до прямой a называют расстояние между точками M₁ и H₁.

Однако чаще встречается определение расстояния от точки до прямой, в котором фигурирует длина перпендикуляра.

Определение.

Расстояние от точки до прямой – это длина перпендикуляра, проведенного из данной точки к данной прямой.

Это определение эквивалентно первому определению расстояния от точки до прямой.

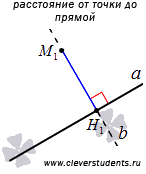
Обратите внимание на то, что расстояние от точки до прямой – это наименьшее из расстояний от этой точки до точек заданной прямой. Покажем это.

Возьмем на прямой a точку Q, не совпадающую с точкой M₁. Отрезок M₁Q называют наклонной, проведенной из точки M₁ к прямой a. Нам нужно показать, что перпендикуляр, проведенный из точки M₁ к прямой a, меньше любой наклонной, проведенной из точки M₁ к прямой a. Это действительно так: треугольник M₁QH₁ прямоугольный с гипотенузой M₁Q, а длина гипотенузы всегда больше длины любого из катетов, следовательно, .

Не нашли, что искали? Воспользуйтесь поиском: