Условия параллельности и перпендикулярности двух прямых; пересечение прямых.

35. Кривые второго порядка: окружность, эллипс.

Окружность. Окружностью называется геометрическое место точек, равноудаленных от одной и той же точки.

Уравнение окружности имеет вид

(x - a)² + (y - b)² = r ²,

где a и b - координаты центра окружности, а r - радиус окружности. Если же центр окружности находится в начале координат, то ее уравнение имеет вид

x ² + y ² = r ².

Эллипс. Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами).

Простейшее уравнение эллипса

где a - большая полуось эллипса, b - малая полуось эллипса. Если 2 c - расстояние между фокусами, то между a, b и c (если a > b) существует соотношение

a ² - b ² = c ².

Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси

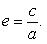
У эллипса эксцентриситет e < 1 (так как c < a), а его фокусы лежат на большой оси.

36. Кривые второго порядка: гипербола, парабола

Парабола. Параболой называется геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая - ее директрисой.

Простейшее уравнение параболы

y ² = 2 px. (*)

Входящая в это уравнение величина p называется параметром параболы. Параметр параболы равен расстоянию от директрисы параболы до ее фокуса.

Координаты фокуса F параболы (*) . (фокус параболы лежит на ее оси симметрии) Уравнение директрисы параболы (*)

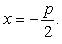
Эксцентриситет параболы e = 1.

y ² = 2 px (p > 0)

Гипербола

Гипербола - геометрическое место точек, для каждой из которых модуль разности расстояний от нее до двух данных точек F₁,F₂ (фокусы) есть величина постоянная, равная 2a.

Элементы гиперболы:
A₁A₂=2a - действительная ось
B₁B₂=2b - мнимая ось
A₁,A₂ - вершины
F₁(c; 0), F₂(-c; 0) - фокусы
F₁F₂=2c - фокальное расстояние

c²=a²-b²

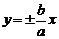- асимптоты
- эксцентриситет. Его можно рассматривать, как числовую характеристику величины раствора угла между асимптотами.
r₁=±(εx-a), r₁=±(εx+a), - фокальные радиусы (верхний знак соответствует правой, нижний – левой ветви)
- директрисы
Каноническое уравнение гиперболы (координатные оси совпадают с осями гиперболы):

Параметрические уравнения:

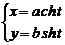
Уравнение гиперболы, сопряженной данной:

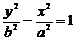
Уравнения плоскости в пространстве (проходящей через точку, перпендикулярно вектору; общее уравнение плоскости; проходящей через три точки; уравнение в отрезках; нормальное уравнение)

Не нашли, что искали? Воспользуйтесь поиском: